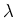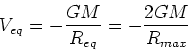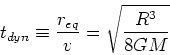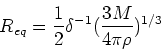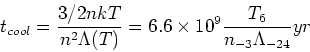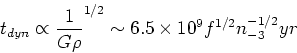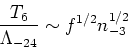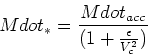

Up: AY616 class notes
Previous: Absorption line systems
Subsections
- Galaxy formation models - general framework of gravitational instability
models. Distinction between dissipationless and dissipational collapse.
Former applies to DM, latter to baryonic; clearly need to understand
baryonic to predict galaxies, but since gravity may be dominated by DM,
must understand dissipationless collapse first.
- Main components:
- Initial conditions
- Dark matter evolution
- Gas evolution
- Star formation and compact object formation
- Feedback: stellar and black hole
- Merging
- Challenges:
- Large dynamic range: stars (
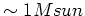 ) to galaxy clusters
(
) to galaxy clusters
(
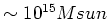 ), structure on sub-pc to 100 Mpc scales
), structure on sub-pc to 100 Mpc scales
- Cosmological model uncertainty: but this is converging, and it
is a model where merging is important, so evolution of objects
cannot be considered in isolation
- Lack of knowledge of detailed physics of black hole formation and
star formation
- Lack of knowledge of detailed physics of feedback
- Because of challenges, neither full numerical nor full analytical
analysis is possible
- Initial conditions
- Dark matter evolution
- Can be calculated numerically, e.g. by N-body simulations. Large
dynamic range poses challenges for direct summation. Various
techniques used to yield results.
- Perturbation spectrum has smaller halos collapsing first on
average, but with significant overlap in collapse times for halos
of different scales.
- As time progresses, significant merging of halos occurs
- Growth of dark matter halos has also been studied using
semi-analytic models, e.g. Bond et al., Lacy & Cole, etc.
These take realization of initial perturbation spectrums and
produce histories of mergers/accretion for objects of different
masses
- Present day dark matter halos characterized by their
mass accretion history (MAH)
- Dark matter halos found to have characteristic density profiles,
often described by the Navarro-Frenk-White (NFW) profile (
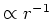 in inner regions,
in inner regions,
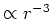 in outer regions.
Transition radius varies for halos of different masses, charactized
by the halo concentration
in outer regions.
Transition radius varies for halos of different masses, charactized
by the halo concentration
- Dark matter halos have some angular momentum; distribution of
angular momentum often characterized by distribution of
dimensionless spin parameter,
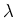
- Gas evolution
- Gas moves in dark matter potentials, but also has pressure, and
can cool, shock, etc.
- Numerical hydrodynamical simulations becoming more and more feasible.
Various techniques used, e.g. smoothed particle hydrodynamics (SPH),
adaptive mesh refinefine (AMR)
- Gas collapses when cooling time becomes short compared to dynamical
time, happens quicker at higher densities and lower temperatures.
Cooling time is relatively short in inner parts of halos, slower
in outer parts
- Various ``semi-analytical'' schemes have been developed to estimate
rate of mass accretion in different dark matter halos, based on
cooling time arguments, etc., e.g. White & Frenk 1991
- Details of cooling are more complex, c.f. numerical simulations,
where gas accretes along filaments, and not at all spherically
- Star formation
- Lacking detailed knowledge of star formation, and lack of
sufficient resolution, star formation is paratemeterized within
models, e.g. based on stability arguments given gas densities
and temperatures
- Parameterization tuned by need to match charactertic observed
relations of observed star formation, e.g. Kennicutt law
- Feedback
- mass function of dark matter halos differs significantly from
mass function of galaxies, suggesting there are processes that
suppress galaxy formation at low and high galaxy masses
- one finds that gas cools and forms stars in
small galaxies early (the ``cooling catastrophe'') and cannot
build up big galaxies
- one also finds that gas may collapse too much in halos, leading
to galaxies that are too small compared with real galaxies
- These problems have suggested the importance of feedback, i.e.
energy deposition back into gas
- Energy from stars within galaxies via stellar winds and supernovae
- Energy from massive black holes
- Energy from surrouding galaxy population, e.g. significant
UV flux to cause photoionization
- Merging
- While merging of dark matter halos can be followed using the
dark matter simulations, merging of galaxies within halos procedes
at a slower rate, because they are centrally condensed
- Merging is increased within a common dark matter halo by the
process of dynamical friction, which transfers angular momentum
from orbiting objects to dark halo
- Merging of galaxies may be important in triggering, and
subsequently cutting off star formation
- Semi-analytic models
- Given various uncertain input physics and parameterizations thereof,
may be productive to use ``semi-analytic'' models to compare with
observed galaxy population
- Initial semi-analytic models done using semi-analytic merging
trees, cooling, star formation, and feedback
- More recent semi-analytic models, e.g. the Millenium
simulation, use numerical dark matter simulations to produce
spatial halo distribution with mass accretion histories for each
halo, then add semi-analytic cooling, star formation and feedback;
these have the advantage of giving large scale environment
- Semi-analytic models starting to reproduce observed luminosity
function, color-bimodality of galaxies, mass-metallicity
relation, Tully-Fisher relation, etc. fairly well. See figures
in Croton et al, MNRAS 365, 11 (2006)
- Numerical models
- Numerical models attempt to capture gas physics more accurately
- they also provide internal structure of galaxies
- realistic galaxies starting to appear in such simulations, but
not yet possible to do large numbers of individual galaxies
within large simulation volumes
Consider analogy to growth of perturbation by gravity in expanding universe
to that in Euclidean space.
General behavior as f(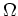 ):
): 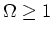 , growth continues
forever,
, growth continues
forever, 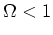 , growth stops at
, growth stops at
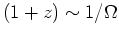 . Sketch
rough curve
for growth of a perturbation.
Schematically sketch a perturbation and discuss relation between density
of perturbation and mass of pertubation.
. Sketch
rough curve
for growth of a perturbation.
Schematically sketch a perturbation and discuss relation between density
of perturbation and mass of pertubation.
Growth of spherical perturbation can be solved analytically. Here,
we simply sketch out some of the main results for the simple case of
spherical perturbations and 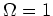 ; full derivations are not shown,
and remember, the preferred current cosmological model does not have
; full derivations are not shown,
and remember, the preferred current cosmological model does not have
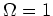 !.
!.
Growth rate given
by Birchoff's theorem of GR ( external matter exerts no force):
where we've defined the overdensity, 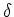 . This applies to
spherical perturbation. This can be compared
with equation for evoltuion of scale factor of the univers
. This applies to
spherical perturbation. This can be compared
with equation for evoltuion of scale factor of the univers
Consequently, perturbation with amplitude 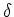 just grows like universe
with different
just grows like universe
with different 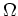 . Integrating equation once, we get
. Integrating equation once, we get
where 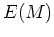 is a constant which is the total energy. Evaluating at maximum
expansion radius, we get
is a constant which is the total energy. Evaluating at maximum
expansion radius, we get
Integrating once more, we get
which, for a perturbation at early times, when 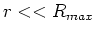 , gives
, gives
As perturbation grows, this growth rate slows down - can write solution
parametrically (not here), similarly to equations for closed and open universes.
For the whole universe,
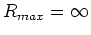 for
for 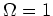 , and
, and
We can now compute an approximate turnaround time, i.e., the time
when perturbation reaches max radius as
In other words, the turnaround time depends on the density, not the mass. All lumps of a given density at a given epoch
collapse at same time.
Consider growth of density.
At early times
we can derive from linear perturbation theory:
and, in terms of overdensity, the turnaround time is
Lumps of higher overdensity collapse first. This growth rate, however,
only applies to the linear regime.
If there were no perturbations on a smaller scale, the perturbation at a given
scale would collapse back to zero radius, i.e. infinite density.
For spherical perturbation, one can compute ``linear perturbation
overdensity'' when this occurs, and find that collapse happens at
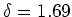 for
for 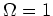 , slightly lower for
, slightly lower for 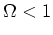 .
.
However, if there's perturbations on smaller scales, these cause random
velocities to be generated, and perturbation settles into equilibrium
configuration given by virial theorem:
giving
where 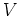 is potential energy
is potential energy
so
Velocity dispersion
Dynamical time
In terms of overdensity using
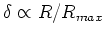 and
and
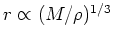 , we get
, we get
These show that if you know the epoch (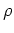 ),
), 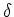 , and mass, you can
get the final equilibrium state.
, and mass, you can
get the final equilibrium state.
In reality, the analytical treatment may be of limited applicability, because
real perturbations aren't spherical.
So now the next question is what is the distribution of overdensities as
a function of mass in the Universe? Usually convenient to express this
in Fourier space, with Fourier coefficients 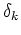 :
:
Generally, many theories
(e.g. inflation) predict that
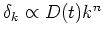 initially,
and that the coefficients have random and independent phases, i.e. a
Gaussian field.
initially,
and that the coefficients have random and independent phases, i.e. a
Gaussian field. 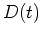 is the growth rate just discussed, which is a
function of the cosmological model. Note also that the inital spectrum
may be modified by physical processes in the Universe, as discussed below,
so the actual power spectrum has a logarithmic slope that changes with
wavenumber, but first let's consider some simple results for a single
power law (which will be roughly applicable to the real case over limited
ranges of scales).
is the growth rate just discussed, which is a
function of the cosmological model. Note also that the inital spectrum
may be modified by physical processes in the Universe, as discussed below,
so the actual power spectrum has a logarithmic slope that changes with
wavenumber, but first let's consider some simple results for a single
power law (which will be roughly applicable to the real case over limited
ranges of scales).
The mean square fluctuation in a sphere of comoving radius R is
where 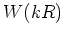 is the window function, which corresponds in this case to the
Fourier transform of a function which is equal to
is the window function, which corresponds in this case to the
Fourier transform of a function which is equal to 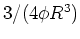 for
for
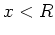 and zero everywhere else. For a power law perturbation spectrum,
and zero everywhere else. For a power law perturbation spectrum,
From this, once can see that if 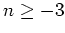 , then small scales collapse
first, i.e. hierarchical clustering.
, then small scales collapse
first, i.e. hierarchical clustering.
We can derive the characteristic mass which is going nonlinear at any
epoch by setting
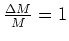 for a general power law spectrum,
and find
for a general power law spectrum,
and find
For
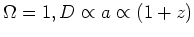 , and we have
, and we have
For a power law spectrum, clustering is ``self-similar''; at any given
epoch clustering looks the same but at a different scale. However, most
cosmological models are not pure power laws. Also, remember this is just
for dissipationless collapse. These simple analytics are for spherical
collapse - which is simpler than what really happens!
What is the fluctuation spectrum for the Universe? One can derive
expression for the potential from above
and one sees that for 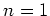 , potential is scale invariant. This
is what is suggested by most inflationary models, and is called the
Harrison-Zeldovich spectrum. However, this spectrum gets modified by
subsequent physical processes.
, potential is scale invariant. This
is what is suggested by most inflationary models, and is called the
Harrison-Zeldovich spectrum. However, this spectrum gets modified by
subsequent physical processes.
First, the universe is not composed of a single species of matter; it
is certainly composed of at least photons and baryons, and likely
composed of at least one species of dark matter. Since the radiation
density declines at a different (faster) rate than matter, at early
times, the density of the universe is dominated by radiation;
matter perturbations will grow at a different rate during that time.
Critical times: epoch of matter-radiation equality, epoch of recombination,
epoch of horizon crossing, epoch at which dark matter becomes non-relativistic
A critical time for the growth of a perturbation is the epoch at which
the perturbation ``crosses'' the horizon, i.e. the epoch at which there
is sufficient time for causal contact across the entire population.
Perturbations grow before this time, but the behavior requires a good
understanding of general relativity and gauge theories. Small perturbations
cross the horizon before large ones.
After horizon crossing, perturbations can begin to grow as described
above. However, perturbations crossing the horizon before matter-radiation
equality have slower growth. In addition,
even after the universe becomes matter dominated, radiation can be
important if the matter is ionized, because in that case it is coupled
to the radiation via Thompson scattering. During this time, perturbations
can be erased as photons diffuse out of the perturbation, a process
known as ``Silk damping''. So baryon fluctuations can't really start
to grow until after recombination.
For dark matter particles, the growth of their perturbations is affected
by their random thermal motions; if these are large, they can prevent
growth from occurring. The random thermal motions are related to the
mass of the dark matter particles. Since we don't know what this is,
dark matter is generically lumped into ``cold'' or ``hot'' dark matter.
Observations of large scale structure suggest that the dark matter
is ``cold''. For dark matter particles, perturbations are damped out
if the velocities are substantial; this is called ``free-streaming''.
Summary: perturbations grow at different rate before horizon crossing, and
smaller scales cross horizon first. In addition, smallest scales which
cross horizon when radiation dominates hardly grow at all until matter
dominates. For baryonic matter, growth is further suppressed until
recombination. For hot dark matter candidates, growth is surpressed
until particles become nonrelativistic.
Growth of perturbations plot.
Final power spectrum plot.
For a given cosmological model, we are interested in calculating the
number of ``galaxies'' as a function of time and mass. Given a Gaussian
field specified by the fluctuation spectrum, one can calculate the
fraction of points surrounded by sphere R in which mean density exceeds
some value. Press and Schecter suggested that if one adopted the linear
overdensity at collapse of a spherical perturbation (1.69) one might
associate this fraction with the fraction of particles which are part
of nonlinear lumps with mass exceeding M. This suggestion, with some
additional fudges, gives rise to the Press-Schecter formalism, which
can be used to estimate the number of collapsed objects as a function
of mass at any given time.
Given reasonable evidence for hierarchical clustering, we know that
merging will be an important physical process. Consequently, it's
of great utility to be able to analytically predict certain merging
characteristics from a given fluctuation spectrum. A way of doing this was
suggested by Bond et al and Lacey and Cole which is being fairly widely
used in semi-analytic models of galaxy formation. The idea is, like for
Press-Schecter, to find a prescription for identifying whether any given
point is part of a nonlinear lump which one might associate with a galaxy
halo. The scheme developed is as follows: for a given realization of the
density field, smooth the field with filters of increasingly larger size,
and compute the mean overdensity for each smoothing size. Associate the
point with the mass of the largest smoothed region in which the
mean overdensity exceeds some critical value, e.g., the linear spherical
collapse overdensity. For appropriate choice of smoothing function, the
mean overdensity as a function of smoothing size is exactly a Brownian
random walk - for other window function, it's approximately random.
Can do this for any point in time by growing realization according
to linear growth law. In practice, it's convenient to think about a
single time-independent realization along with a threshold overdensity
which decreases with time. Looking at random walk in such a picture
gives a semi-analytic merging history
(Lacey and Cole Fig 1). The nice
thing about this formalism is that it allows one to calculate analytic
expressions for a variety of interesting quatities: the probability than
an object with given mass with merge with an object of some other mass
as a function of time, the probability that an object of some mass will
be included as part of an object of a larger mass at some later time,
the distribution of formation times of objects with given mass, the
distribution of survival times of objects, etc. Examples: merger rate
(LC Fig 3
and
Fig 4):
mergers with small halos dominate numerically,
but mass accretion rate is dominated by mergers with halos of higher
mass. Survival time
(LC Fig 5):
small halos can survive a long time
(wide distribution of survival times), but big halos are unlikely to -
they have a much narrower distribution. Halo formation times (definition:
a halo forms when it has accreted half of it's current mass)
(LC Fig 6
and
Fig 10):
small halos form earlier.
Assess truth of such semi-analytics through N-body simulations. Find
that assumption of associating single particle with halo isn't good,
but statistical association is good! Discussion of numerical techniques
and limitations.
One final piece of information is needed for us to proceed with a model
of galaxy formation, which is the distribution of matter within a
given lump. A simple approximation which is found via numerical simulations
to be poor, is to take it to be an isothermal sphere, with
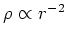 , out to the virial size of the lump. From numerical
simulations, it appears that all hierarchical models produce halos with
a characteristic density profile, known as the Navarro, Frenk, and White
(NFW) profile, which has
, out to the virial size of the lump. From numerical
simulations, it appears that all hierarchical models produce halos with
a characteristic density profile, known as the Navarro, Frenk, and White
(NFW) profile, which has
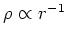 in the inner regions, and
in the inner regions, and
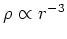 in the outer regions.
in the outer regions.
Note that this density profile may be further affected by the presence
of baryons within the halo, as they collapse further (via dissipation)
and then can act to gravitationally compress the dark matter halo (adiabatic
compressions).
To compare with real observable galaxies, we need to consider dissipation.
Cooling of gas allows baryonic matter to collapse further within a virialized
halo, and this collapsed gas should correspond to observable galaxies.
For gas to cool within a dark halo, the cooling time must be less than the
crossing time, otherwise cooling will not occur. For a uniform cloud,
the cooling time is given by:
where 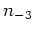 is the density in units of
is the density in units of
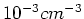 and
and
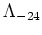 is the cooling in units of
is the cooling in units of
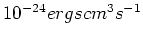 .
.
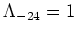 is roughly the minimum cooling rate for a primordial
plasma at
is roughly the minimum cooling rate for a primordial
plasma at 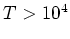 K. The dynamical time is given by
K. The dynamical time is given by
where 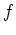 is the gas fraction of a cloud. Seting the two time scales to
be equal gives
is the gas fraction of a cloud. Seting the two time scales to
be equal gives
which, with a crude appoximation for the cooling curve, is
At higher densities and lower temperature, the cooling time is shorter.
From the virial theorem, the relation
between mass, temperature and density of a cloud is given by:
for 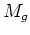 in solar masses. Hence, our cooling criterion suggests that
dissipational collapse will occur only for objects with
in solar masses. Hence, our cooling criterion suggests that
dissipational collapse will occur only for objects with
where 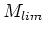 is the limiting dark matter halo mass. Note that for small
is the limiting dark matter halo mass. Note that for small
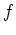 , this roughly corresponds to galaxy masses!
, this roughly corresponds to galaxy masses!
One can proceed with this crude defintion of galaxies. If one identifies
galaxies as all objects at a given time with 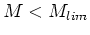 , one can use
the Press-Schecter formalism to derive the relative number of galaxies
as a function of mass and epoch, i.e., a luminosity function. However,
a problem arises. If all halos under the limiting mass turn into galaxies,
one finds that at early times almost all of the mass is in such halos, so
everthing turns into small galaxies early, and no gas is left to form big
galaxies later! This has been called the cooling catastrophe. It's
actually not so bad because the smallest halos are too cool to cool
effectively and so might survive. However, it seems likely that some
mechanism is needed to reduce the efficiency of galaxy formation.
, one can use
the Press-Schecter formalism to derive the relative number of galaxies
as a function of mass and epoch, i.e., a luminosity function. However,
a problem arises. If all halos under the limiting mass turn into galaxies,
one finds that at early times almost all of the mass is in such halos, so
everthing turns into small galaxies early, and no gas is left to form big
galaxies later! This has been called the cooling catastrophe. It's
actually not so bad because the smallest halos are too cool to cool
effectively and so might survive. However, it seems likely that some
mechanism is needed to reduce the efficiency of galaxy formation.
A common proposal is that energy input from supernovae ejects gas from
systems before it all turns into stars. Presumably, such an effect
would work more effectively for systems with lower binding energy. If
one postulates that some fraction of the gas mass is ejected with is
proportional to the binding energy (which is 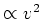 ), then one can
derive a revised luminosity function. Using Press-Schecter,
White and Rees derived such a relation and found that they could derive
a Schecter-like form for the galaxy luminosity function. This is very
encouraging! However, they derived a faint end slope of
), then one can
derive a revised luminosity function. Using Press-Schecter,
White and Rees derived such a relation and found that they could derive
a Schecter-like form for the galaxy luminosity function. This is very
encouraging! However, they derived a faint end slope of
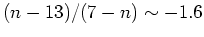 , which is considerably steeper than the observed
value. Note that this contains no estimate for merging, however.
, which is considerably steeper than the observed
value. Note that this contains no estimate for merging, however.
This whole cooling argument is quite crude, however, as it doesn't even account
for the distribution of gas within a halo and the corresponding realization
that the cooling time is a function of location. In fact, the inner parts of
halos cool rapidly, and the cooling radius gradually moves out as a function
of time. Given this, we can estimate the rate at which gas accretes onto
an existing halo, which is a prerequiste for a star formation rate. The
maximum accretion rate is the rate at which is halo is growing out of
the surrounding material, and is given by
However, if the cooling time in the outer halo is long, then material
can only accrete in a slower cooling flow. This rate is given by
At a given 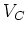 , cooling is more efficient at higher redshift and for
larger gas fraction. The rate of accretion will be the smaller of the
two rates: if the cooling time is shorter than the infall time, the infall
rate limits the rate of accretion, if the accretion time is shorter, than
cooling limits the accretion. Small halos are infall limited, large
halos are cooling limited
(white and frenk Fig 2).
, cooling is more efficient at higher redshift and for
larger gas fraction. The rate of accretion will be the smaller of the
two rates: if the cooling time is shorter than the infall time, the infall
rate limits the rate of accretion, if the accretion time is shorter, than
cooling limits the accretion. Small halos are infall limited, large
halos are cooling limited
(white and frenk Fig 2).
Note that detailed cooling for galaxy formation is sensitive to metallicity,
since critical temperature regime is where cooling is very sensitive to
metallicity. This requires some model for chemical enrichment.
Finally, to model galaxy formation, we need to estimate how much of the
infalling gas turns into stars, and account for the feedback from star
formation. This is required to prevent the cooling catastrophe. A variety
of scenarios have been suggested. At a minimum, we require a process which
keeps too much gas from cooling. At a maximum, we might have a scenario
in which gas in a halo is expelled entirely. Generally, supernovae is the
mechanism invoked to inject energy. Unfortunately, it is very poorly
understood with what efficiency energy is deposited. It can be parameterized
by:
where 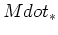 is the rate at which stars form. The minimum requirement is
that this energy balance the energy associated with the
dissipational losses for the component of the matter which does not
form stars. This gives
is the rate at which stars form. The minimum requirement is
that this energy balance the energy associated with the
dissipational losses for the component of the matter which does not
form stars. This gives
where 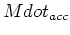 is the smaller of the accretion rate or the cooling rate.
One can then solve for the star formation rate:
is the smaller of the accretion rate or the cooling rate.
One can then solve for the star formation rate:
One then might consider whether to distribute such star formation uniformly
over time or in a bursting fashion.
WF Fig 3, SF higher at earlier
epochs but note this doesn't have information about abundance of halos.
Alternatively, one might wish to allow some fraction of the cold gas to
stay in the form of cold gas, i.e., not form stars. To do this one would
need to assume some actual star formation law, such as the Kennicutt law.
A very simple parameterization is to take
where 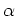 is a free parameter, and
is a free parameter, and 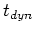 is a characteristic dynamical
time scale for the galaxy. One can then include feedback with some
assumed energy per supernovae and number of supernovae given an IMF and
the star formation rate. The numbers here are also very uncertain, so the
feedback rate must also generally be considered to be a free parameter.
is a characteristic dynamical
time scale for the galaxy. One can then include feedback with some
assumed energy per supernovae and number of supernovae given an IMF and
the star formation rate. The numbers here are also very uncertain, so the
feedback rate must also generally be considered to be a free parameter.
Once one decides on a star formation prescription, one can calculate actual
brightnesses and colors as a function of time for each galaxy using
stellar population synthesis models.
Finally, one needs to consider how to handle galaxies inside of halos which
merge over time. Since these are in the centers of the potential wells, it's
likely that the individual galaxies will not merge as fast as halos merge.
A simple approximation to make is that all individual galaxies survive
during a halo merging event, but that galaxies merge as time proceeds by
the process of dynamical friction. This case can be parameterized as a
merging rate proportional to the dynamical friction timescale for each
galaxy, with a proportionality constant which is a free parameter to
allow for uncertainties in orbit radii, etc. The simplest model just defines
the most massive galaxy in a halo merger event to be the dominant galaxy,
while all other galaxies are satellites which can eventually merge with the
dominant galaxy, but not with each other. This is clearly a fairly crude
approximation. One also needs to consider what happens to gas as it falls
into a halo which has several galaxies in it; again, a simple, crude
assumption is to have all of this gas go to the dominant galaxy, so star
formation in satellite galaxies just dies out as their gas is depleted and
is not replenished. This simple picture actually reproduces many features of
observed galaxies! In addition, one can add features which allow all of the
cold gas to turn into stars at the time of a merger to simulate starbursts,
etc.
It's now possible to combine all of the aspects we've discussed into a
coherent model for galaxy formation which might be compared with real
galaxies. The different components are: 1) an estimate of the abundance
of halos and merging rate as a function of mass and time, from PS or
excursion set calculations given a cosmological model, 2) a cooling
model for star formation inside of halos, 3) a model for how to handle
merging of galaxies, 4) a prescription for how to assign morphologies
to galaxies. For the following discussion, I am going to describe
models constructed by Kauffmann, Guideroni, and White. They choose to
identify ellipticals/bulges with galaxies that merge with comparable
masses, with the critical ratio, 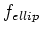 as a free parameter. Their
models, which are comparable with other models, then have the following
free parameters: efficiency of star formation, efficiency of feedback,
parameter for dynamical friction merging of galaxies, parameter for what
to identify as spheroidal systems, cosmological parameters (
as a free parameter. Their
models, which are comparable with other models, then have the following
free parameters: efficiency of star formation, efficiency of feedback,
parameter for dynamical friction merging of galaxies, parameter for what
to identify as spheroidal systems, cosmological parameters (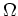 ,
,
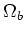 ,
, 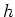 , normalization,
, normalization, 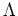 , etc.).
, etc.).
Generally Kauffmann et al have been considering CDM models. They proceed
as follows. First they identify halos which have 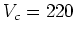 km/s, for which
they want to reproduce quantities observed for the Milky Way and its
companions. First, they adjust the star formation and feedback efficiency
to make the dominant galaxies within such halos match the brightness and
neutral gas content of the Milky Way. As the star formation efficiency is
increased, the galaxy gets brighter. As both star formation and feedback are
increased, more cold gas is lost. So one can tune both parameters to match
the observed quantities. Then one can look at the luminosity function of
objects within the halo, corresponding to the MW and its companions. One
finds that the model has far too many low mass neighbors if no galaxy
merging is included
(KWG Fig 1).
If merging is included one can bring
down the number of galaxies, but it brings down the number of brighter
neighbors faster than fainter neighbors, so it also does not match the
observations well. They are able to get a match only by inhibiting galaxy
formation in small halos. There are plausible mechanisms for doing this,
such as background ionization at early epochs from quasars, or possibly
from more extreme feedback in smaller halos. KWG get reasonable agreement
by inhibiting SF in halos with
km/s, for which
they want to reproduce quantities observed for the Milky Way and its
companions. First, they adjust the star formation and feedback efficiency
to make the dominant galaxies within such halos match the brightness and
neutral gas content of the Milky Way. As the star formation efficiency is
increased, the galaxy gets brighter. As both star formation and feedback are
increased, more cold gas is lost. So one can tune both parameters to match
the observed quantities. Then one can look at the luminosity function of
objects within the halo, corresponding to the MW and its companions. One
finds that the model has far too many low mass neighbors if no galaxy
merging is included
(KWG Fig 1).
If merging is included one can bring
down the number of galaxies, but it brings down the number of brighter
neighbors faster than fainter neighbors, so it also does not match the
observations well. They are able to get a match only by inhibiting galaxy
formation in small halos. There are plausible mechanisms for doing this,
such as background ionization at early epochs from quasars, or possibly
from more extreme feedback in smaller halos. KWG get reasonable agreement
by inhibiting SF in halos with 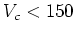 km/sec at
km/sec at 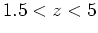 . They
then compare colors of objects with the observations
(KWG Fig 2). Generically, the
hierarchicial clustering models predict redder colors for lower mass
galaxies. This is understandable, since SF is turned off when objects merge
in the model, so only the largest objects have ongoing star formation, and
hence blue colors. The general trend is observed in real galaxies, but there's
a conflict for the dominant galaxies, which are generally too blue in the
models. However, note that the models don't have dust or chemical enrichment,
both of which might make for redder objects.
. They
then compare colors of objects with the observations
(KWG Fig 2). Generically, the
hierarchicial clustering models predict redder colors for lower mass
galaxies. This is understandable, since SF is turned off when objects merge
in the model, so only the largest objects have ongoing star formation, and
hence blue colors. The general trend is observed in real galaxies, but there's
a conflict for the dominant galaxies, which are generally too blue in the
models. However, note that the models don't have dust or chemical enrichment,
both of which might make for redder objects.
One can then proceed to apply the model to other objects. Kauffmann et al
compare with the Virgo cluster, and find reaonable agreement with the
observed luminosity function for the same parameters
(KWG Fig 3), except that they
form a central galaxy which is much brighter than M87; to avoid this, they
have to put in an ad hoc modification which turns off star formation in
very massive halos. The models also approximately predicts the right
percentages of E/S0 galaxies as a function of magnitude
(KWG Fig 4).
The model can also be used to predict a Tully-Fisher relation
(KWG Fig 7), and
reasonable agreement can be found. In this model, the TF relation arises
from the relation between star formation and feedback, and the good
agreement arises partly because the model is normalized to the Milky Way.
A significant problem with the model is that the mean luminosity density
of the model is roughly a factor of two higher than that of the real
universe. This comes because there are too many faint galaxies. This may
be a result of the cosmological model adopted.
One can use the same model to see if one can understand the faint blue
galaxies. This sort of model naturally predicts a steepening of the LF
at higher redshifts even without merging, since star formation is turned
off in smaller galaxies as their halos merge with larger ones. Reasonable
fits can be found to the observational data, especially for models which
can reduce the number of faint galaxies at present.
Finally, lets consider the issue of elliptical galaxy formation. In the
model, we form spheroidal systems by roughly equal mass mergers. If this
merged galaxy is the dominant galaxy, it will quickly accrete gas and
become a ``spiral''. However, if its halo merges again with a more massive
halo, the elliptical can passively evolve. The question is whether such
a model for elliptical formation is consisent with the lack of spread
in the Mg-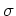 relation. One finds that in clusters, the luminosity
weighted mean age of the ellipticals are all pretty old
(Kaffmann MN 281, 487, fig 1),
but that in the field, brighter E's are younger
(Fig 2).
Interpretation is clear: in field galaxies continue to accrete gas.
This makes field ellipticals quite different from cluster ellipticals;
cluster Es have stopped accreting gas and will evolve passively, but
field Es continue to accrete and may turn into spirals! The models are
consistent with the lack of scatter observed in elliptical colors or
line strengths. However, the model predicts that this scatter will get
significantly larger at
relation. One finds that in clusters, the luminosity
weighted mean age of the ellipticals are all pretty old
(Kaffmann MN 281, 487, fig 1),
but that in the field, brighter E's are younger
(Fig 2).
Interpretation is clear: in field galaxies continue to accrete gas.
This makes field ellipticals quite different from cluster ellipticals;
cluster Es have stopped accreting gas and will evolve passively, but
field Es continue to accrete and may turn into spirals! The models are
consistent with the lack of scatter observed in elliptical colors or
line strengths. However, the model predicts that this scatter will get
significantly larger at 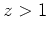 .
.
(Klypin).
N-body codes: direct, PM, PPPM, ART. Size and resolution (spatial and
temporal)
Gas dynamics: SPH vs. hydro codes.
Stellar physics...


Up: AY616 class notes
Previous: Absorption line systems
Jon Holtzman
2007-05-04
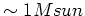 ) to galaxy clusters
(
) to galaxy clusters
(
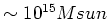 ), structure on sub-pc to 100 Mpc scales
), structure on sub-pc to 100 Mpc scales
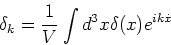
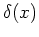 is overdensity at different locations.
Inflation predictes
is overdensity at different locations.
Inflation predictes
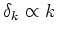 (Harrison-Zeldovich
spectrum)
(Harrison-Zeldovich
spectrum)
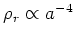 ) dominated
matter density (
) dominated
matter density (
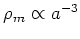 ). Suppresses
growth of smaller perturbations.
). Suppresses
growth of smaller perturbations.
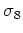 : rms mass perturbations on
: rms mass perturbations on 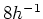 Mpc scale, and constrained by various large scale structure
observations.
Mpc scale, and constrained by various large scale structure
observations.
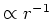 in inner regions,
in inner regions,
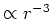 in outer regions.
Transition radius varies for halos of different masses, charactized
by the halo concentration
in outer regions.
Transition radius varies for halos of different masses, charactized
by the halo concentration