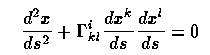
Before going on to galaxy formation and evolution, it is worthwhile to look at the connections between cosmological models and basic tenets of general relativity for the commonly-considered instance of an expanding Universe in the Friedman model. The connection between the world model and observables comes about from Weyl's postulate - that the wordlines of galaxies form a 3-bundle of non-intersecting geodisics orthogonal to a series of spacelike hypersurfaces. This is what is now generally meant by a comoving coordinate systems, since we appreciate that galaxies and clusters depart from this ideal through having nonzero peculiar motions. An excellent source for this material is Peebles' Physical Cosmology (Princeton 1971). Pedantically, using the relativistic coordinates xm , a spacelike hypersurface satisfies x0=constant, and a worldline which follows the Weyl condition has xm constant for m=1,2,3. This constrains the geometry of spacetime (i.e. the fact that these exist and can be orthogonal) such that the connections g between coordinates g 0 m x0 xm = 0 where we use the relativistic summation convention for repeated indices. For the metric ds, this implies that the governing equation
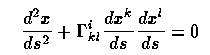
reduces to (for m=1,2,3) G 0 0 m = 0. This in turn means that the three spatial coordinates are equivalent, so g00=g00x1, and this is conventionally taken as 1. This gives a metric - the expression connecting spacetime intervals with their components in some coordinate system - the form
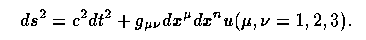
If we incorporate the cosmological principle that the result is homogeneous and isotropic, we reach the Robertson-Walker metric
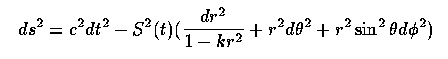
where we also transform for convenience into a spherical set of spatial coordinates. Here, S is a scale-factor (clearly time-dependent, but location-independent by construction through invoking the Cosmological Principle), and k is determined by the large-scale curvature. This is conventionally folded into the constant of integration in the denonimator of the term in dr², although the choice is sometimes made of letting this express the curvature radius R (positive, negative, or infinite) such that k= 1/R².
Integration for the behavior of components of the interval between events in this metric yields
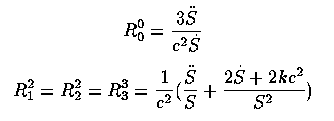
Including the energy equation to relate mass-energy density and curvature, on can derive analytical solution for k=0, ± 1. For k=0 (equivalent to infinite radius of curvature) we have the Einstein-de Sitter model, at critical density, for which S ~ t2/3 and t0 = 2/3H as we've noted before. Given enough justification, one may add a cosmological constant L to the expressions for Rm above, which gives the Lemaitre model; depending on L, the Universe can hang for a long time at nearly constant R before settling on an asymptotic late-time solution of the familiar Hubble expansion.
Last changes: 11/2000 © 2000