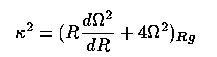
A detailed understanding of the internal working of galaxies must incorporate their dynamics - just how the gravitational potential and internal motions balance to give galaxies their forms. This is all from Newton's laws at work, but distributed masses can give results that violate intuitions honed on the inverse-square law. All of this is treated well and exhaustively by Binney and Tremaine. The key is that observable stars and gas move in response to the total potential of the mass. Major surprises have come from recent observations both of spirals and ellipticals.

Local density: Close to the disk plane, if we adopt a reference frame sharing the local rotational velocity, stellar motions consist mainly of small oscillations about the mean location (or guiding center) - shades of Ptolemaic astronomy! Radial, tangential, and vertical oscillations may occur, with the vertical frequency not in general matching the in-plane motion as it would for small perturbations to a Keplerian orbit (because galaxies have extended mass distributions). Small radial oscillations (epicycles) have an axial ratio 2:1 (tangential:radial extent - we'd have been in real trouble if Hipparchus had tried that for the planets instead of perfect circles). The epicyclic frequency is given by

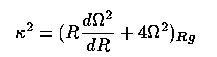
in which R_g is the mean radius of the orbit's guiding center. Vertical oscillations through the disk plane are of particular interest, with an instantaneous period for a given z-velocity set by the surface density within the region covered by the orbit. In the limit of a disk with infinitely thin mass profile, this case may be analyzed as simple harmonic motion, with the frequency n of z-oscillations given by

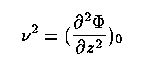
where F is the potential. For realistic cases, the oscillations are slower because the particle orbits do not sample the whole mass distribution. In the real Universe, the two frequencies will not be commensurate, leading to a three-dimensional space-filling trajectory within a roughly toroidal region for small excursions about the guiding center. The frequency is an easier quantity to work with than v_z, since various kinds of star have different scale heights, and scattering from molecular clouds should increase a population's scale height with time while the potential stays essentially unchanged. In the case of our galaxy, the surface density so measured is known as the Oort limit. This gives about 90 solar masses/parsec² within 700 pc of the plane, and implies a local density for matter of 0.15 solar masses per cubic parsec, which is slightly more than known stars and gas. A recent detailed analysis, including scale heights for various kinds of stars, is in Bahcall 1984 (ApJ 276, 169 and 287, 926). The need for invisible matter in the galactic disk has fallen with improved data - note that this does not apply to the halo "dark matter" problem, which is as glaring as ever.

Differential rotation: For anything but solid-body rotation, the angular velocity O(R) is a function of R, so the detailed configuration of objects in some region is "stretched" with time by differential rotation. This makes small-scale spiral structure practically inevitable in a rotating disk (as in Seiden and Gerola's models for flocculent spiral patterns). We can measure this effect in our own neighborhood via stellar proper motions and radial velocities using the Oort constants A and B , defined by

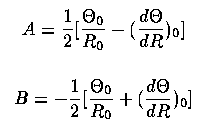
in which Q is the (linear) rotational velocity and R is the distance from the disk center, both evaluated in this case at our galactocentric distance R₀. Nearby stars will show systematic patterns in radial velocity v_r and proper motion parallel to the galactic plane m_l with galactic longitude l:

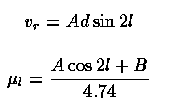
in arcseconds per year for m_l. Here, d is the star's distance. From stellar statistics, A ~ 15 km/s kpc and B ~ -11 km/s kpc. [Recent analysis of Hipparcos data by Mignard 2000 A&A 354, 522 shows changes with distance penetrated for A, from 11-14.5 km/s kpc for early dwarfs to late giants, and B from 13.2-11.5 respectively.] From these, adopting a distance to the galactic center gives the rotational velocity at the Sun's location. Taking R₀ = 8.5 kpc gives sQ₀ = 245 km/s, so our period about the galactic center is

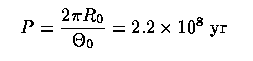
which is at least consistent with VLBI measurements of the proper motion of the compact radio source at the galactic center. Also of interest is the local gradient

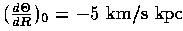
for comparison with other galaxies.

Viewing a differentially rotating disk from outside, the velocity field shows a characteristic symmetric "butterfly" pattern, whose contours may be open or closed depending on the form of the rotation curve. Solid-body rotation gives parallel, straight velocity contours. Ripples superimposed on this are occasionally seen and may be expected near spiral arms, due to spiral density waves and their potential ridges (Lin and Shu 1964 ApJ 140, 646). Such waves are one of the solutions to the problem of how spiral structure can survive for times oong compared to the time taken to wind up a material feature in a differentially rotating disk, with various specific analyses (such as the swing amplifier of Toomre) most relevant for particular kinds of dynamics. Note that all global spiral patterns where we can check are in fact trailing, though individual leading arms can be found in perturbed systems and weak reflected leading modes have been identified in grand-design spirals. An example of the impact of spiral structure on disk velocities is seen in M81, where velocity ripples are seen near the spiral arms (data from Visser 1980 A&A 88, 159, reproduced from the ADS):

This effect may limit the accuracy of local determinations of the Oort constants.

Rotation curves: For a tracer mass orbiting in a spherical potential, Kepler's laws and a useful theorem of Newton's give

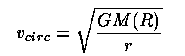
where M(R) is the mass interior to radius r. If the orbit is outside most of the mass distribution, we expect the circular velocity to approach the ordinary Keplerian case v ~ 1/r^1/2 as in the solar system. This is used to invert the rotation curve v(r) and thus by differentiation or modelling to obtain the mass distributions M(r), r (r) in disk galaxies. In realistic models, v_c depends at the 20% level on the flattening of the potential, as shown in figs. 2-12 and 2-17 of Binney and Tremaine.

The more flattened the mass distribution, the flatter the rotation curve - the less it acts like a point mass. Rotation curves of real disk galaxies, once it was possible to measure them to large radii, gave one of the big surprises of modern astronomy. M(r) continues to increase with r almost as far as can be measured. A first hint came when the rotation curve of the Milky Way was pieced together from optical, H I, and CO observations (from Burton 1976 Ann. Rev. 14, 275, shown from the ADS):

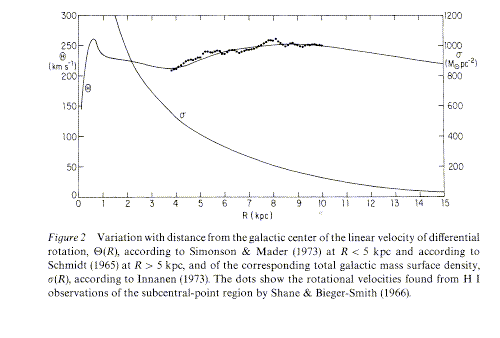
Here, there is little evidence of a Keplerian drop at large radii. A flat rotation curve implies r(r) ~ 1/r², though in the interior of all but the dimmest dwarf galaxies the luminous mass must dominate over the dark matter. This behavior is universal among spirals. Here's a sample in NGC 5746,from Lowell imaging and Kitt Peak optical spectroscopy:

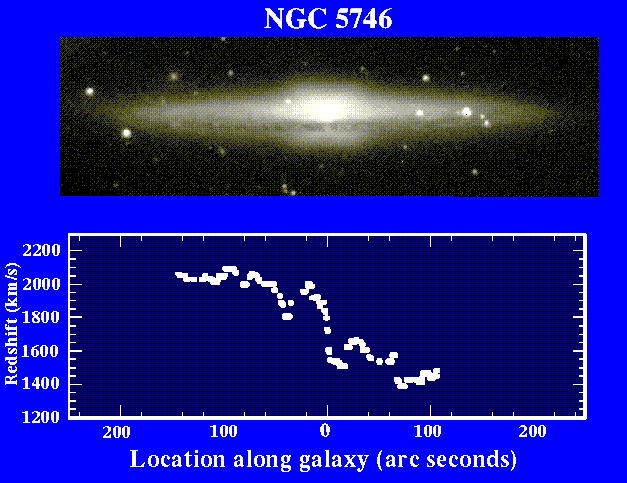
and further ones as found by Rubin and collaborators, shown in Fig. 3 of Rubin, Ford, and Thonnard 1978 ApJL 225, L107 (reproduced courtesy of the AAS):

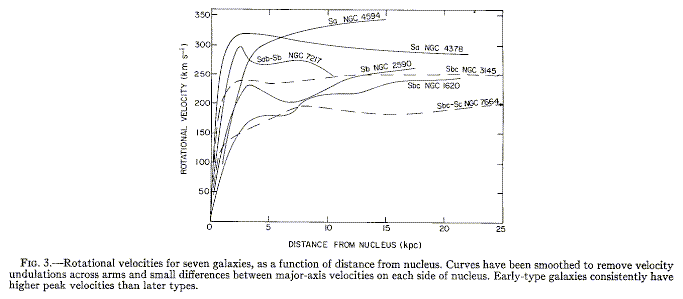
In the most extreme cases, the rotation curve is flat to almost 100 kpc. Clearly, most of the mass is in a more extended distribution than stars or gas - the "missing mass" (even though what is missing is in our brains, not in the mass). There are trends of the mass distribution with Hubble type, as mapped by Rubin et al 1985 ApJ 289, 81: the form of the rotation curve is fairly constant, with the amplitude changing from Sa to Sc. The maximum rotation velocity has median values 299,222,175 km/s for Sa, Sb, and Sc, respectively. In all cases, the correlation with luminosity dominates for individual galaxies. It is traditional to trace some aspects of the mass distribution via the mass-to-light ratio M/L in solar units, running from a few for young stellar assemblies to several hundred for galaxy halos and clusters. Not only does this reduce the big galaxy-small galaxy bias, but it is also distance-independent for traditional dynamical mass estimates.

After hearing so much about "flat rotation curves", it is important to point out that many spirals don't show flat forms - they show more or less linearly rising rotation patterns over much of the disk, especially for the numerically domiannt low-luminosity late-type spirals. I'll illustrate this with part of a random page from the immense data paper by Mathewson, Ford, & Buchhorn (1992 ApJS 81, 413, courtesy of the AAS, as usual):

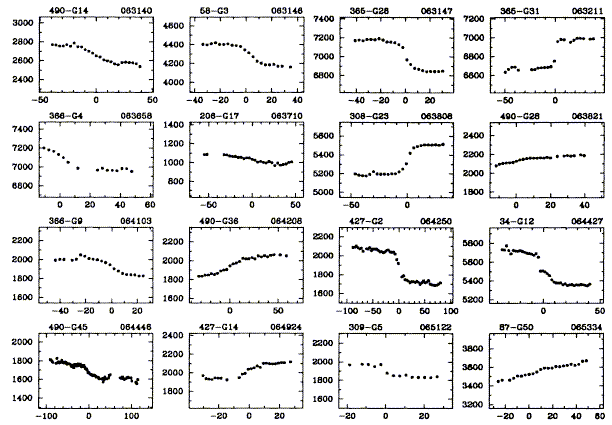
One might also ask whether the disparity can be explained if it's not the mass that's missing, but our understanding of gravity. After all, we have no experimental verification of how gravity works beyond 50 AU (well it seems to work fine for globular cluster internal motions, so we could call that a confirmation at scales of tens of parsecs) or at extremely small accelerations. Milgrom has asked this repeatedly, proposing a modified Newtonian dynamics (MOND) in which there is a minimum possible acceleration in response to a gravitational potential. However, the fact that gravitational lensing in clusters gives the same masses as both virial motions and X-ray gas equilibrium makes it very difficult to concoct an alternate scheme that still satisfies Occam's Razor. This notion's stock did rise somewhat when McGaugh and de Blok 1998 (ApJ 499, 41; this manuscript was placed on the LANL preprint server with the authors' comment "This result surprised the bejeepers out of us, too") found dynamical properties of some extreme dwarfs in reasonable accord with Milgrom's predictions.

A crucial property of disks when we consider their response to tidal perturbation is that they are dynamically cold - that is, the internal velocity dispersion of disk stars (or gas) is very small compared to the circular velocity (at the level of 0.05 in the ratio for population I stars in our vicinity, for example). Another term from the jargon is "rotationally supported", as contrasted with "pressure-supported" for dynamically hot elliptical systems. This means that perturbed stars will continue to fly in formation as they follow changed orbits. This accounts for the spectacular bridges and tails seen in interacting spirals, and the equally spectacular lack of such narrow features in disturbed pairs of elliptical galaxies. This sample calculation is taken immodestly from Howard, Keel, Byrd & Burkey (1993 ApJ 417, 502).

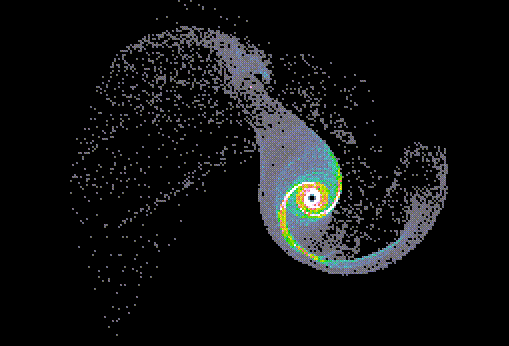
Last changes: 9/2001	  © 2000