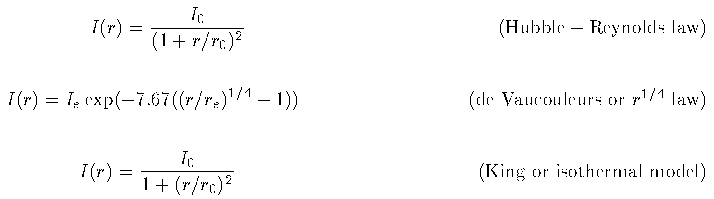
Several morphologically (and sometimes kinematically) distinct components emerge from the images of galaxies: for disk galaxies, these may include nucleus, bulge, lens, and disk. The disk may itself contain arms, a bar, rings, and other embellishments. The relative roles of these in some cases change with Hubble type. Some of these (i.e. disk-bulge luminosity ratio) were discussed by de Vaucouleurs (1977, Yale Conf. p. 43) under the rubric of "quantitative classification".

For S0 and spiral galaxies, we may broadly consider a disk and a central bulge. The disk is quite thin both in stars and gas (when present), with aspect ratio 10 or greater (beware photographic and visual effects in getting such numbers from pictures, however - the "real" axial ratio seldom exceeds 6). The bulge is more nearly spherical, though it is sometimes found to be a (triaxial) ellipsoid like a very stubby bar. A "classical" approach to separating the bulge and disk contributions for some galaxy with measured intensity I(x,y) = I(r,q) starts by assuming a typical functional form for each. Bulges and elliptical galaxies usually follow similar radial distributions of intensity, parameterized by any of the following:

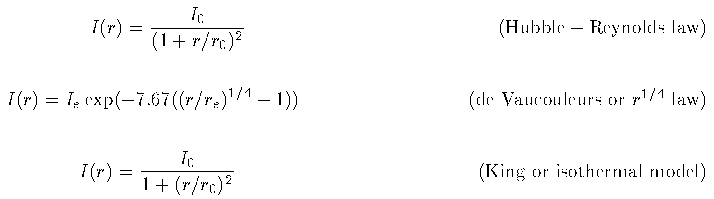
Hubble and de Vaucouleurs profiles are purely empirical representations of typical data, without accompanying dynamical models. The last at least has a physical justification even if it has infinite total luminosity - the assumption of isothermal and isotropic stellar velocities, derived for globular clusters by King 1966 (AJ 71, 64). For an untruncated King model, the luminosity density r(r) follows the simple form

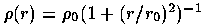
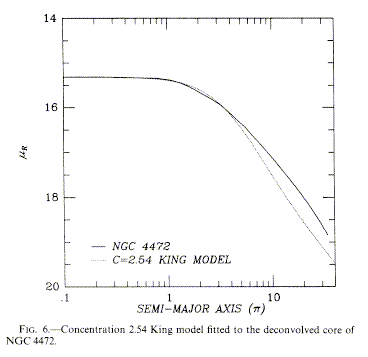
The King model incorporates a core radius which has interesting dynamical implications. Some ellipticals (such as M87) have unmistakeable cores, within which the intensity distribution is nearly flat, while others show scale-free profiles to the limit of even HST resolution. When distinct cores are present, they are very seldom of a pure King-law form, flattening toward zero central slope, as shown in Fig. 6 of Lauer 1985 (ApJ 292, 104) (reproduced below by permission of the AAS).

Driven by extensive HST imaging of galaxy cores, Lauer et al. (1995 AJ 110, 2622) have introduced a more complicated form, the "Nuker" profile, to represent such cores as two asymptotic power laws (an outer one of slope -b and an inner one of slope -g shading into one another (over an area controlled by a parameter a) at a characteristic break radius r_b:

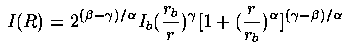
It is also worth mentioning that the form introduced by Jaffe (1983 MNRAS 202, 995) has the huge virtue of being analytic in both its density and surface-brightness L distributions as well as finite. In these expressions, the radius r is given in terms of the radius within which half the light is emitted (Jaffe gives 1.31 times the effective radius as derived from the light profile), and the surface brightness is at projected distance a in the same units:

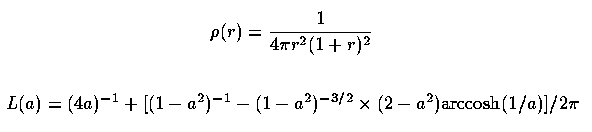
The mechanics of measuring intensity profiles for galaxy images have been treated by Lauer 1985 (ApJSuppl 57, 473), Davis et al. 1985 (AJ 90, 169), and Jedrzewski 1987 (MNRAS 226, 747). The last algorithm is implemented in the STSDAS isophote package. There are numerous subtleties to worry about, such as the effect of seeing in producing an apparent core where none exists (Schweitzer 1979 ApJ 233, 23; 1981, AJ 86, 662) and accurate sky subtraction, particularly with CCDs that may not cover the whole galaxy at once. Also there are numerous ways to mess up the intensity calibration - it is rare to find agreement among observers better than 5% even for bright galaxies.

Disks are frequently fit with an exponential surface brightness profile

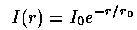
Sersic showed that the exponential and de Vaucouleurs profiles may be seen as special cases of a distribution now bearing his name:

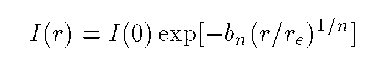
Here, the parameter n is a concentration index. This function has often been used when dealing with poorly resolved galaxies, or when it is not clear that either of the two kinds of fits just discussed is appropriate. Recent work suggests that it may be a generally useful function which in fact describes galaxy spheroids better than the classic de Vaucouleurs or King laws.

There is a major limitation to the use of such fitting functions: what if you took an inappropriate form for bulge or disk? Many galaxies obviously pay no attention to these equations. Kent 1985 (ApJS 59,115) introduced a more general approach useful for galaxies seen strongly inclined to our line of sight. This relies on the different shapes of bulge and disk, starting with minor and major axis profiles as first estimates and generating successively closer approximations of each. Sometime a distinct small disk component (the visual lens) appears. Further, many disks are not terribly exponential in distribution - fits as a power law minus constant are just as successful, and may be more physically reasonable. Likewise, there are central regions in some late-type spirals than are closely exponential in form (sometimes called pseudobulges, in case they have a different origin). One should beware of too much interpretation of empirical equations!

Besides bulge and disk components, intermediate structures (such as the visual lens) may appear. These are shown in the K-band profile of VV188=NGC 4438 (which is much messier optically than in the near-infrared). The plot is from Keel and Wehrle 1993 (AJ 106, 236), courtesy of the AAS.

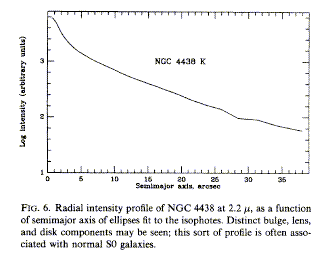
A pure exponential disk would be a straight line, as in the outer part of the profile. A gentle excess above this outside the bulge may be considered a lens component (or a gross departure of the disk from an exponential form). There is no basic reason that such components need be physically distinct; don't push the easy formulas too hard.

Further difficulties are encountered in decomposing very late-type or dwarf systems, in which one must avoid the effects of very luminous resolved stars and clusters, or use star counts themselves rather than intensities. Some examples are given in Eskridge 1988 (AJ 95, 1706 and 96, 1336, 1352) and for near-IR work, Giovanardi and Hunt 1988 (AJ 95, 408). For earlier type spirals, care is also needed with inclination effects - internal dust may distort the disk profile as our viewing angle becomes closer to the disk plane. In fact, Disney et al. 1989 (Nature 239, 939) have speculated, and Valentijn 1990 (Nature 346, 153) has strongly claimed that typical spiral disks are optically thick (opaque) to visible light, which conclusion has strong implications on everything from mass-to-light ratios (we see only half the stars) to interpretation of IR emission (lots of hidden ordinary stars mean less need for IR starbursts). This conclusion is also demonstrably wrong. Further work (for example, the whole volume on "The Opacity of Spiral Disks", ed. Davies & Burstein, NATO ASI ser. C, 469, Kluwer 1995) suggests a picture with much of the obscuration concentrated in the same place as the brightest blue stars - the arms - and more modest distributed obscuration in between. White, Keel, & Conselice (2000, ApJ 542, 761) find evidence that this component is close to an exponential with a scale length similar to that of the starlight (which is where the dust has to come from in the first place). We deal with dust at length later in the course.

All these problems aside, decompositions of galaxy images yield some simple parameters that vary as functions of Hubble type. One commonly encountered one is disk/bulge luminosity ratio (or bulge/disk ratio), a function of wavelength since in general disks can be blue and bulges are red. This correlates well with both Hubble type and Yerkes type, since its visual analog of concentration is part of each classification. Note that exceptions do occur, such as NGC 7331 in which the bulge is luminous but of large scale length. Ellipticals have no visual disk (or they'd be called S0s) but some show weak "pointy" isophotes that may be signatures of very weak disks (and some are "boxy" which may be a fossil of merging). Conversely, Sc and Sd systems have almost no bulge light. de Vaucouleurs 1977 (Yale Conf.) followed Fig. 2 of Yoshizawa and Wakamatsu (1975 A&A 44, 363, reproduced from the ADS) in making this point:

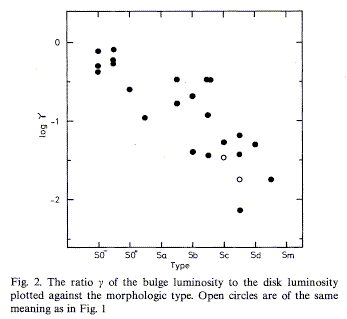
The most interesting thing is not that we could recognize bulges and disks photographically, but that seemingly disparate properties such as spiral-arm morphologies correlate with bulge/disk ratio. Some theorists broadly consider exponential profiles to result from dissipative collapse, and the elliptical-like profile to be largely nondissipative.

Bulge/disk ratios may be used as part of a fully quantitative classification scheme, paralleling but not fully mimicking the Hubble sequence. The major distinction remains that between bulge = pop. II = halo population (more or less) and disk = pop. I = recently formed stars. Note that studies of M33 have shown that there is not necessarily a continuity between nucleus, bulge, and spheroid populations (van den Bergh 1991 PASP 103, 609).

Principal-component analysis has been applied to data such as diameter, surface brightness, and central concentration by Watanabe et al. 1985 (ApJ 292, 78), Bujarrabal et al. 1981 (AA 104, 1) and Whitmore 1984 (ApJ 278, 61). Spirals and ellipticals are each mostly specified by two components, which are mixtures of directly observed quantities.

There has been some interesting exploration of image decomposition in the Fourier domain as well. This is especially useful if one wishes, for example, to examine the coexistence of various spiral modes m=1,2,3... in a disk. A sample is shown by Iye et al. 1982, ApJ 256, 103. The object is to decompose the whole 2-dimensional intensity distribution, not just the locations of strong peaks along the arms. Further applications have been used (for example, by the Elmegreens, 1993 PASP 105, 644 and 1995 ApJ 445, 591) to examine the relative strength of the even and odd modes in various parts of a disk, sometimes suggesting a change when crossing resonant locations.

Several kinds of functions have been fitted to spiral arms' shapes (traced by starlight, H II regions, or H I). A logarithmic spiral r ~ log[q] is a frequent contender, but there is so much variation (and so few grand-design spirals) that the local pitch angle seems more useful. There is a strong correlation between pitch angle and stage along the Hubble sequence; this was illustrated by fig. XX of van den Bergh's book. A correlation is hardly a surprise since this was one of Hubble's criteria, and more explicitly one of the major criteria for de Vqaucouleurs' revision. The pitch angle may correlate with surface density (Ma 2002 A&A 388,389).

In fitting spirals, accurate knowledge of the disk inclination and any warp present are crucial; M31 changes from a one-armed leading to 2-armed trailing spiral when its kinematic warp is taken into account. Galaxies with a sparse population of spiral tracers have especially ambiguous structures; it takes lots of beads to define an invisible string.

Two-dimensional fitting can be used to constrain morphology at faint levels, or in the presence of complicated instrumental response functions, by asking how many components are needed to fit the full two-dimensional structure to a statistically meaningful level. Some examples are given in Keel & Windhorst 1993 (AJ 106, 455) and, for the HST Medium-Deep Survey, by Naim et al 1997 (ApJ 487, 510); and Casertano et al. 1995 (ApJ 453, 599).

As shown in the M81 images atop the classification page, some of the quantities we've been decomposing are strong functions of wavelength, particularly bulge/disk ratio. Classically this has been done in the optical band, but sometimes (as in very dusty IR-bright galaxies, see Scoville et al. 2000 AJ 119, 991 and their data pages), we are driven to use wavelengths where there's actually something to be seen. Ellliptical galaxies generally show only the most subtle structural changes, but of course spirals become more bulge-donminated at longer wavelengths, while bulges sometimes disappear in the UV. There have been several recent surveys which should eventually put this on a quantifiable bases (for example the Ohio State survey). Extension to the near-IR is especially important, since dust penetration and changes in stellar population can make the disks look quite different. One initial attempt at a near-IR Hubble diagram was done using 2MASS images (rather shallow in surface-brightness sensitivity) by Jarrett (2000, PASP 112, 1008).

Once again, note that all these exercises can in principle be done in any passband. It's common to use differences in disk scale length at various wavelengths to measure age, metallicity, or extinction gradients (depending on the passbands and one's level of understanding of the system). Ryder & Dopita (1994 ApJ 430, 142) applied it to compare the distributions of current star formation (from azimuthally averaged H-alpha images) to the integral of past star formation (from optical continuum images), to test whether gas is being depleted by star formation uniformly or from the outside inward (they come down on a remarkably uniform behavior, by the way).

Last changes: 8/2006	  © 2000-6