- Initial conditions: usually assume no heavy elements, and pure gas (ie.,
no stars).
- Star formation history: Birthrate function
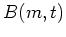 gives number of stars
formed with mass m per volume. Usually split into separable function:
gives number of stars
formed with mass m per volume. Usually split into separable function:
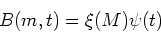
where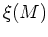 is the initial mass function, and
is the initial mass function, and 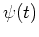 is the star
formation rate; this implicitly assumes an IMF which is constant in time,
which may or may not be true, but so far, there's no strong observational
evidence against it (but note pop III issues).
is the star
formation rate; this implicitly assumes an IMF which is constant in time,
which may or may not be true, but so far, there's no strong observational
evidence against it (but note pop III issues).
- For any particular star, we use stellar evolution to compute amount and
composition of mass returned to the ISM vs. amount locked up in stellar
remnant (
Pagel Figure 2, from Maeder 1992).
Note that the rate of return depends on stellar mass, especially
for the case of SnIa, which also depends on the binary fraction.
- nucleosynthesis: main element groups and their sources:
- light elements: BBN
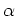 elements: massive stars (core collapse SN)
elements: massive stars (core collapse SN)
- Fe-peak elements: type Ia SN and core collapse SN
- s and r process (neutron capture) elements: core collapse SN, AGB stars...
- Note that infall might arise from primordial clouds, or from processed
material, e.g., mass-loss from halo stars. Outflow might come from
supernovae winds, and in this case, it's possible that the composition
of outflow material might be more enriched than the typical composition
at any given time. So things can get complicated.
- Allowing for all sorts of realistic effects makes it difficult to
make very simple predicions for the evolution of abundances. However,
under some simplifying assumptions, it is possible to do so. A simple
chemical evolution model serves as a useful baseline against which observations
can be compared to determine where the assumptions may break down.
In addition, understanding a simple model allows us to introduce and
become acquainted with terminology that is is widespread usage.
- Consider a total mass M, split into a gas mass
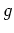 and a total stellar
mass,
and a total stellar
mass, 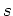 . For a simple model, we'll consider that that gas at any
time is well mixed.
. For a simple model, we'll consider that that gas at any
time is well mixed.
At any given time, we wish to know the fractional abundance
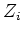 of element
of element 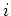 .
Consider an inflow rate into the system,
.
Consider an inflow rate into the system, 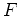 , and outflow (ejection) rate,
, and outflow (ejection) rate, 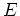 .
Then we have:
.
Then we have:
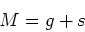
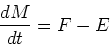
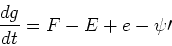
where is the star formation rate in units of mass per time,
is the star formation rate in units of mass per time,
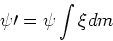
and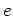 is the ejection rate of mass from stars,
is the ejection rate of mass from stars,
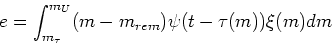
which is a sum over all stellar masses of the product of the star formation rate at the time of formation of each mass with the mass returned to the ISM, weighted by the IMF. The lower limit of integration is at the stellar mass which is dying at time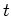 ; lower mass stars don't contribute
because they haven't ejected any mass yet. We also have,
; lower mass stars don't contribute
because they haven't ejected any mass yet. We also have,
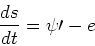
since the mass in stars increases by the number of stars formed, but decreases by the amount of mass lost back to the ISM from the previous generation of stars. For the elements, we have
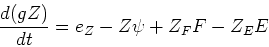
since the mass in each element increases by the amount released by previous generations and added by inflow, but decreases by the amount locked up in new stars and lost to outflow. The term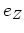 is given by:
is given by:
![\begin{displaymath}e_Z = \int_{m_L}^{m_U} [(m - m_{rem})Z(t-\tau(m)) + mq_Z] \psi(t-\tau(m)) \xi(m) dm\end{displaymath}](img139.png)
where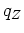 represents the fractional mass of element
represents the fractional mass of element 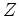 synthesized and
ejected during stellar evolution (so left term in brackets gives material
which returns unprocessed and right term gives newly synthesized contribution).
In a simple model, the synthesized masses are independent of the metallicity
of the population (although we know this is not true for some elements, more
on this later).
synthesized and
ejected during stellar evolution (so left term in brackets gives material
which returns unprocessed and right term gives newly synthesized contribution).
In a simple model, the synthesized masses are independent of the metallicity
of the population (although we know this is not true for some elements, more
on this later).
- To simplify, consider an approximation to these formulae called the instantaneous recycling approximation which assumes that all elements
are returned instantaneously - good for products of massive stars,
but less good for products from lower mass stars, e.g., iron. Then we have
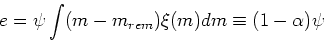
where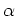 is the lock-up fraction of mass locked up in remnants:
is the lock-up fraction of mass locked up in remnants:
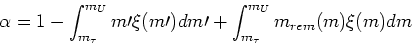
where the second term is the total mass in stars which have died, and the third term is the mass from those stars which has been locked up in remnants. Alternatively, one can think of the return fraction,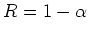 .
This gives us
.
This gives us
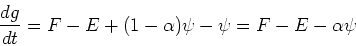
We also have
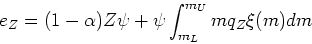
We define the stellar yield,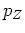 , to be
, to be
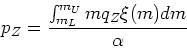
so the yield give the fraction of the remnant population synthesized and released in each element. This gives us
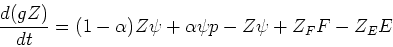
where rhs terms are recyled material, new production, lock-up in new stars, inflow, and outflow. Simplifying, we have:
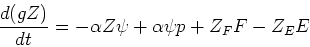
Using mass locked up in stars, , as the independent variable
, as the independent variable
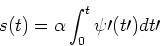
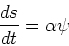
so we get
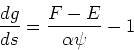
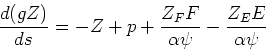
If we make a further assumption of a uniform wind,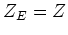 , then
, then
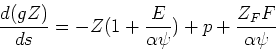
and, finally,
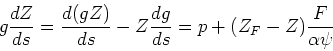
or, alternatively,
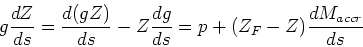
This is a basic equation of chemical synthesis. - The simplest model for chemical evolution assumes no inflow or outflow, a
homogeneous system without any spatial differentiaion of metallicity, zero
initial metallicity, and yields which are independent of composition. This
is known as the Simple, one-zone model.
In the Simple model, we have
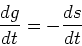
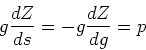
Solving for Z(g), we get
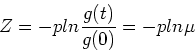
where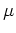 is the gas fraction
is the gas fraction
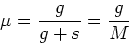
The average abundance in stars is:
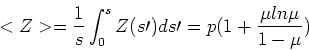
which tends to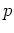 as
as 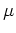 becomes small, i.e., the gas fraction becomes
small. For larger gas fractions, the mean
becomes small, i.e., the gas fraction becomes
small. For larger gas fractions, the mean 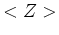 will be lower than the
yield. Note that this is the mean metallicity weighted by stellar mass,
not by stellar luminosity or by number, but these could easily be derived.
will be lower than the
yield. Note that this is the mean metallicity weighted by stellar mass,
not by stellar luminosity or by number, but these could easily be derived.
- Brief digression into units people use for measuring abundances:
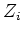 ,
,
![$[Fe/H]$](img166.png) ,
, 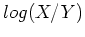 ,
,
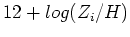 .
.
- The chemical evolution relation holds for any element, so the ratio
of the abundance of
any two elements should be the ratio of the yields and constant in
time. This seems to be true for some elements, e.g. Ne and S (
Pagel Fig 5,
Pagel Fig 6),
but not for others, e.g. C (
Fig 7). This is likely caused
by a changing yield of carbon with metallicity because, e.g., of mass
loss.
- However, this relation doesn't seem to hold for Fe (
Fig 9), which
is plausibly explained by a significant fraction of Fe coming from SnIa,
which have a time delay
and so the simple model with instantaneous recyling doesn't hold. This
is important to realize, because many direct ``metallicity'' determinations are
made from Fe lines. If SnIa is the right explanation, one would expect
a constant ratio of Fe/O for systems in which star formation proceeded
rapidly (i.e., finished before SnIa go off), but in systems with more
extended star formation, Fe/O would increase at higher O abundance.
(
Pagel Fig 10). Different
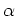 /Fe ratios are indeed found in populations that are thought to
have formed over a short period of time (e.g. globular clusters).
/Fe ratios are indeed found in populations that are thought to
have formed over a short period of time (e.g. globular clusters).
- Most elements go in lockstep with O (
Fig 11).
- The constancy of element abundance ratio holds for primary elements,
i.e. those that are produced from primordial abundance. In addition,
some elements are secondary, which means that some element must
previously exist in order for the secondary element to be created. An
example is N, which is produced during the CNO cycle in greater abundance
with a larger initial abundance of C. This is observed (
Fig 12).
Another prediction of the simple model is that abundances should increase as gas fraction decreases, with the slope of the relation giving the yield. A relation with the correct trend is observed in a sample of irregular and blue compact galaxies ( Fig 13), but the derived yield is much lower than predicted from stellar evolution; this may arise from lower yields at low metallicity or from preferential mass loss of processed material (e.g., from supernovae) in these low mass systems. If we consider the luminosity of a system to be related to the gas fraction, we might expect a relation between luminosity and abundance, which is in fact observed (fig 14).
Sometime people talk about the ``effective yield'' of a system, which is the yield derived from application of a simple model to data.
If we have the gas fraction decreasing as one goes towards the center of spiral galaxies, we expect to observe a metallicity gradient in the sense of the observed one. Note that the gradient in stars, as measured by the mean metallicity, is significantly shallower than that in gas.
The simple model predicts an increase of the metallicity with time. The
rate of increase depends on the rate of star formation. If we assume
that the SFR is proportional to the gas mass,
![]() , with
, with
![]() a constant, then we get
a constant, then we get
and we expect the abundance to increase linearly with time. This trend is roughly observed (Pagel Fig 17) in MW disk stars, albeit with large scatter.
The simple model can be used to predict the number of stars expected as
a function of metallicity. Rewriting our basic equation
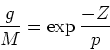
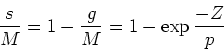
Differentiating with respect to Z, we ge
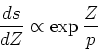
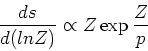
which is a prediction for number of stars as a function of logarithmic abundance. This relation seems to work pretty well for field stars in the Galactic halo ( Fig 19), but only with a very low yield. This can be explained if one includes continuous mass loss from the halo system with a mass loss rate which is proportional to the star formation rate. Plausibly, this gas would flow into a disk and form disk stars. However, there's almost certainly not enough mass coming from the halo to form the entire disk. The metallicity distribution in the bulge also appears to fit a simple model reasonably well (Fig 22).
However, the distribution of disk field stars does not fit the simple model well at all. The problem is that there are too few observed low metallicity stars, and is commonly known as the G-dwarf problem (Fig 23). There are several possible solutions: time-dependent yields, a finite initial enrichment (or ``prompt initial enrichment'' from gas inflowing from the bulge or halo or a different initial IMF), or, probably most popular, inflow models. (fig 23 shows several inflow models).
General applicability, or lack theeof, of simple chemical evolution models. Utility of chemistry for ``fingerprinting'' populations.