 FIGURE
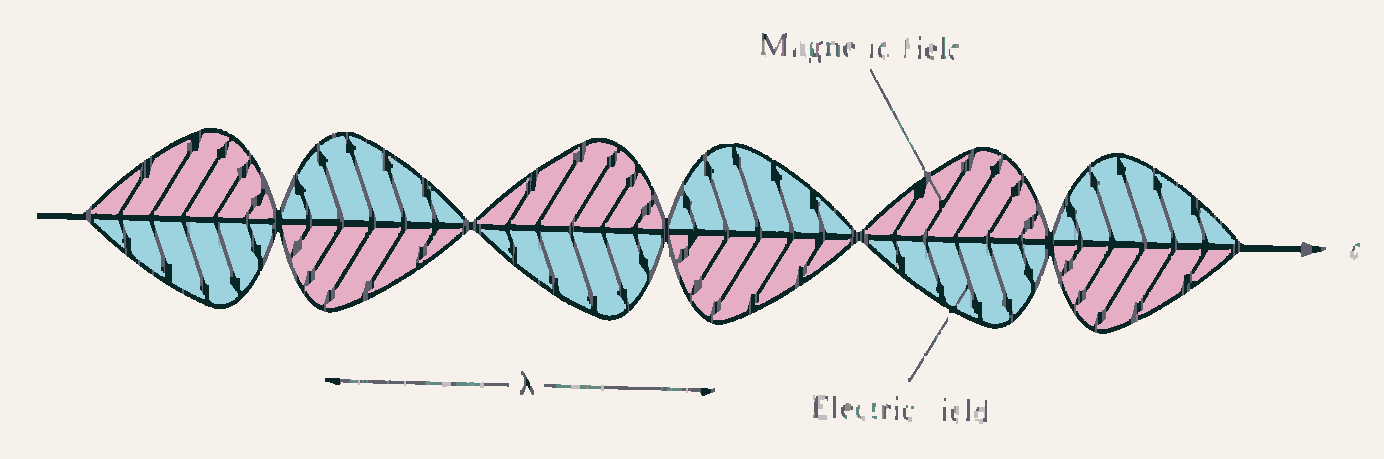
FIGURE Light consists of alternating electric and magnetic fields moving through space at the speed of light. The distance between the peaks is the wavelength of the light.
At the end of this section you should understand the following:
Review questions on light:
Basic Properties of Light
Light is very important to astronomy, and for obvious reasons. Astronomers are not able to go out and sample the objects of their study, namely stars and galaxies (an exception can be made for the study the solar system). All they can do is sit here on Earth and observe the light which comes from those distant objects. Fortunately, that light contains a huge amount of information. But to interpret that information we have to understand what light is, how it is generated and absorbed, and how it propagates through space. Light was a mystery to early scientists. What is it? What is it composed of? Well, let us first observe that light is something we call energy that is radiated through space; hence, light is radiant energy. We often think of different kinds of light as if they were completely different things: Heat radiation, visible light, tanning rays, X-rays. But these are all different manifestations of light.
Since light is energy radiating through space we next need to consider whether it travels instantaneously or at some finite speed. Early attempts to measure the speed of light were not successful, basically because the speed of light, as we now know, is very large. The speed of light is designated by the character c , and it is about equal to 300,000 kilometers per sec (km/s). The finite speed of light was demonstrated for the first time by astronomical means, specifically by noting the observed time lags in the orbits of Jupiter's moon when Jupiter was further away from the Earth.
Is light a particle or some sort of a "wave" in some unknown substance? Isaac Newton thought that light had to be composed of particles, in part because a light beam projected through a hole didn't spread out through space like sound waves or water waves would. However, in 1803 Thomas Young passed light through two narrow slits and produced a wave interference pattern of alternating dark and light bands, a pattern that is created only by waves. This seemed to settle the matter, although, in fact, light is both a particle and a wave. Let us see how these two natures manifest themselves.
The most significant breakthrough into the nature of light was achieved by James Maxwell. Maxwell was studying the behavior of electric and magnetic fields. He found that a time-varying electric field could generate a magnetic field and vice versa. He was able to put together a set of equations that described this behavior. What he found from his equations was that alternating electric and magnetic fields traveled through space at a speed that was equal to the speed of light. Maxwell's great leap of intuition was to conclude that light was composed of the same things that made up electric and magnetic waves. Indeed we now refer to light as electromagnetic radiation.
Can we make the idea of electromagnetic fields a little more familiar? Most people are acquainted with magnets and hence magnetic fields. Electric fields are produced by things with electric charge. Both electric and magnetic fields can produce forces that attract and forces that repel. What Maxwell showed was that a field that is changing in intensity with time will generate the other kind of field. This is, for example, how electric generators work: spinning magnets create electric fields which drive electric currents. Now in the case of light, one has the magnetic and electric fields without the magnets or the individual electrical charges. The fields are constantly fluctuating, generating each other and propagating through space. The fields move through space at the speed of light. Electric and magnetic fields are types of energy, and they can propagate through space, hence light is energy radiating through space.
 FIGURE
FIGURE
Light consists of alternating electric and magnetic fields moving
through space at the speed of light. The distance between the peaks is
the wavelength of the light.
We speak of light as a wave phenomenon; if you like, think of light as waves of electric and magnetic field moving through space. Other waves you might be familiar with include sound waves (which move at the speed of sound) and water waves (which too have a wave speed). Light and all waves are characterized by their wavelength which is the distance from one wavecrest to the next. Wavelength is generally designated with the Greek letter lambda and is measured in units of distance. Frequency is the other measure of a wave, and it is the number of waves that pass a given point per second. Frequency is designated by the Greek letter and is in units of inverse time (e.g., ``cycles per second''). A cycle per second is the unit of frequency and this is known as a ``Hertz.'' Since all light waves travel at the speed of light one can see that wavelength and frequency must be related to each other, for if waves of light of a certain wavelength are going past you at the speed c you will see a number individual wavecrests go by in one second that is given by the speed of light divided by the wavelength. Hence for light the frequency and wavelength are related by the formula:
(Frequency) x (wavelength) = (speed of light)
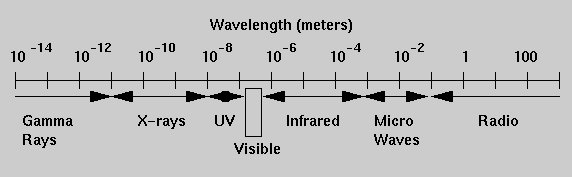
Although we tend to think of light as just the visible white light that we see with, light comes in a complete spectrum of types, the electromagnetic spectrum. Each "flavor" of light is characterized by a particular wavelength. The visible spectrum is composed of light of different colors (the rainbow colors) and the wavelengths of this light ranges from about 700 nanometers to 400 nanometers. The long wavelength (lower frequency) end is the red light and the short wavelength (higher frequency) end is the blue light. In traveling through a prism, light is bent by the glass but the amount of bending depends on the light's wavelength. This is what spreads the white light out into the separate colors. (The same thing produces a rainbow with the raindrops acting like tiny prisms). But there are many more flavors of light than just the visible spectrum. To the long wavelength side (beyond red) is the infrared (which you know as heat radiation), microwaves, and radio waves. FM radio has a higher frequency than AM radio for example. At wavelengths shorter than violet we have the ultraviolet (sunburning rays) and then X-rays and then gamma rays. The later examples give some hint that somehow the energy of the given type of light is also tied in to its wavelength since at least in terms of biological damage X-rays are worse than UV, and gamma rays are the worst of all. And indeed, the shorter the wavelength (or higher the frequency), the greater the energy of the light.
FIGURE
Different wavelengths of the fluctuating electromagnetic waves
correspond to different types of light in the electromagnetic spectrum.
The visible portion of the spectrum is a small region from about 400 to
700 nanometers (billionths of a meter). Different astronomical objects
emit most of their radiation in different parts of the spectrum.
Today's astronomer studies the sky in all wavelengths.
We have been speaking of light as a wave and indeed it is. But modern physics has shown that light also acts like a particle because it comes in minimum-sized packets, individual "particles" of light which are called photons. In particular, it was Einstein's explanation of the photoelectric effect that introduced the photon to modern physics. For some purposes it is best to think of light as a wave, but for others it is best to think of it as a bunch of little photon particles. This particular nature of light becomes most important when discussing matter emitting or absorbing light since it can do so only in these discrete amounts. Specifically the energy of each photon of light of a given frequency is expressed by Planck's law:
(Energy) = hc / (wavelength)
where h is a number called Planck's constant. Planck's constant is a very tiny number (which means that each individual photon carries a very small amount of energy). But Planck's law expresses the fact that a photon of ultraviolet light is much more energetic than a photon of red light. For that matter blue light is much more energetic than red and this has an effect in photography. Photography works by having photons pass through a camera and land on a film that has chemicals that undergo changes when they absorb a photon of a given wavelength. In color photography the chemicals have to react only to a narrow range of photon wavelengths. Because red photons carry less energy per photon it is harder to get them to react with chemicals, making it more of a challenge to get a good color film that does reds well. As another example, a gamma ray photon can really do damage to biological cells by wrecking the molecules that they smash into. Visible light photons however do not have the energy to smash apart those molecules. This is something you already know: gamma rays and X-rays are dangerous to biological organisms (e.g. you).
You may protest that light has to be one or the other, either a wave or a particle. But light is whatever it is; we are describing what its observed behavior is like. Under many circumstances light behaves like a wave and has observed wavelike properties such as wavelength and frequency. When it is absorbed or emitted it behaves like a particle in that the "amount" of light is always in discrete units we call "photons." One uses whatever picture, wave or particle, that best describes the observed phenomenon. (Remember the parable about the blind men and the elephant.)
The Emission of Light
We now know something about the general nature and property of light. But how does light get produced? Specifically we must consider the subject of the emission of light from objects (and its inverse, the absorption of light by objects). The whole subject of the emission, absorption, and interaction of light with matter is pretty complicated. We will focus on a few specific processes that are very important for astronomy.
The first kind of light emission we will consider is the so-called ``thermal emission'' or blackbody radiation. A blackbody is defined to be a perfect thermal emitter---it would be black because an ideal emitter would also be an ideal absorber. The radiation given off by a blackbody is determined solely by its temperature. If you were to shine a light onto a blackbody it would absorb the photons and then reradiate their energy as light appropriate to the temperature of the blackbody.
How does a blackbody work? As an approximate picture of what is going on think of the atoms and molecules that make up all matter. They are in a constant state of motion, a thermal (related to heat or temperature) motion; that is, they are "jiggling" or vibrating about. The amount of motion is characterized by an object's temperature: the higher the temperature, the faster the molecules and atoms move about. Now recall that light is changing electromagnetic fields. The electrons and nucleons that compose atoms are charged and if they are moving they might generate varying electric and magnetic fields. The faster they move, the more rapid the change in the fields and hence the higher the frequency of light. Although the actual situation is rather more complicated, this provides a rationale for the basic fact of thermal radiation: the higher an objects temperature, the higher the frequency of the light it emits (hotter equals bluer).
As an experiment, go find an electric range. Turn it on low and wait for a few moments then place your hand over the heating element. You can feel heat radiation coming up from the unit. This is infrared radiation being emitted from the coil. Your skin acts as an infrared detector. If you turn the heat up eventually coil begins to glow dull red (take your hand away!). Now in addition to the infrared radiation some noticeable amount of red light is being emitted. If you turn it up further the coil glows orange as more visible light is emitted. You also know that the temperature of the coil has increased throughout this experiment. One might imagine that if there were even higher settings on the stove you could get a white hot burner. In principle you could imagine turning the temperature up until you got mostly gamma rays (this would be a temperature in excess of ten million degrees). Hence the higher the temperature of a blackbody emitter, the higher the frequency (or shorter the wavelength) of the predominant light it emits. The relation between temperature and the dominant wavelength of the light emitted by a blackbody is called Wien's law. It is expressed as
(Peak Wavelength in centimeters) = 0.29/T.
Note that the wavelength is measured in centimeters and the temperature as degrees Kelvin. Because of the inverse relation to the temperature one sees that as the temperature goes up the peak wavelength goes down.
Now thermal radiation is not emitted only at the peak wavelength. There is a complete spectrum of radiation emitted; it simply has a peak at the wavelength given by Wien's law. The sun is nearly a blackbody thermal emitter with a temperature of about 5800 Kelvin. This corresponds to a peak wavelength of 500 nanometers which is right about at green (right in the middle of the visible band of light; coincidence or what?).
As a blackbody sits and emits radiation it is radiating away photons, and hence energy. In fact a blackbody is trying to come into temperature equilibrium with its surroundings. If it absorbs more photons of higher energy, then it heats up. If it emits more than it absorbs, then it cools down. The sun is sitting in space with a surface temperature of 5800K radiating photons into space (which has a temperature of about 3K). So the sun is trying to cool down by the emission of light. The energy carried off by the light is replaced by nuclear reactions within the sun.
It is relatively simple to characterize the amount of energy a blackbody gives off. This is important in trying to compute the total energy emitted by the sun, that is, its luminosity. If you add up all the light emitted by a blackbody then you would get the total energy flux carried by that light. There is a specific formula that describes this energy flux, and that is the Stefan-Boltzmann law, which states that the total energy per second per unit emitting surface area in light from a blackbody is proportional to the temperature to the fourth power:
(Flux of Energy) = sigma T4.
Sigma is a constant called the Stefan-Boltzmann constant. Because the energy flux goes as the temperature to the forth power, a hotter blackbody gives off a lot more energy than a cooler blackbody. For example, if star A is the same size as star B but twice as hot at the surface, it is giving off 16 times as much blackbody radiation energy as B.
Flux is energy per unit area, so a computation of the total energy given off by a star requires knowing how big the star is (which is why in the above example we said that stars A and B had the same size). As an example we can write that the total energy per second from the blackbody radiation of the sun is equal to the sun's surface area times the Stefan-Boltzmann law:
L = 4 pi R2 sigma T4
where R is the radius of the sun, L is the luminosity of the sun, and T is the temperature of the sun. So redoing our example from above, now assume that star A has half the radius of star B and twice the temperature. How do their luminosities compare? Because the ratio of their radii is 1/2 and radius is squared in the formula, shrinking a star by 1/2 reduces its luminosity by a factor of 4. But doubling the temperature increases the flux by a factor of 16. The combination of the two effects now makes star A 4 times as luminous as star B.
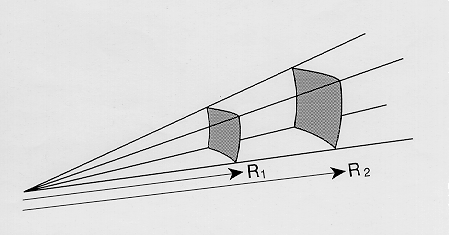
The Stefan-Boltzmann law potentially gives us a way of determining the radius of star. We can determine the temperature by means of the peak in the blackbody spectrum. Next we can measure the amount of energy received here at the Earth. This is some small fraction of the total energy emitted, i.e., the luminosity of the star. The light of the star spreads out through space over a larger and larger area, specifically, at a distance R from the star, the area of a sphere of radius R, i.e., 4 pi R2. If we capture some small amount of the star's light in a telescope, the ratio of the area of the telescope to the area of that huge sphere will be the ratio of the amount of light we capture compared to the total amount of light emitted. Thus if we know the distance to the star we know its luminosity. Using the Stefan-Boltzmann law we can then compute the radius.
FIGURE
Light from a source spreads out in space. The further from the source
the less light per unit area there will be (the source is not as
bright). The brightness drops off as one over the distance squared.
This is called the inverse square law.
Note that high luminosity stars that have low temperature must, therefore, be quite big. Red Giant stars are an example of a low surface temperature star that have huge sizes (hence the name "Red Giant").
Up to now we have been concerned with thermal radiation. The thermal emission spectrum is called a continuum spectrum because light is emitted over a continuous region of the spectrum. The light from a blackbody is the sum of all the photons emitted from all the molecules and atoms packed together into a solid body. But what if you were to look at the light coming from an individual atom? Then what you would see would be a bit different. Most people have some picture of an atom consisting of a nucleus surrounded by orbiting electrons (like a small solar system). However, the electrons have to be in certain orbits, they can't be in just any orbit (this is a "quantum mechanics" effect and is related to the fact that energy, i.e. photons, comes in discrete packets). When an electron jumps between orbits in an atom a discrete photon of light is emitted or absorbed. (See Figure 4-16 of the text.) The light is emitted if the electron jumps to a lower energy orbit (moves closer to the atom) and light is absorbed if the electron moves to a higher energy orbit: if you like, the photon comes in and knocks the electron up a notch. The difference of the energies of the two orbits is equal to the energy of the photon. This means that the light emitted or absorbed has a definite wavelength and hence color. The exact energy of the electron orbits depends on the particular atom the electron attached to, hence different atoms emit or absorb different wavelengths of light. These wavelengths are known as emission lines, or for absorption absorption lines. By observing specific emission or absorption lines one can learn that certain elements are present. This means one can analyze the contents of, say, a cloud of interstellar gas solely from the study of the light emitted or absorbed by that cloud.
Now we come to some basic statements about the various spectra of light that one can observe. We have discussed three types: the continuous spectrum such as given off by a black body, e.g., the sun, an emission spectrum, when atoms emit discrete colors of light, and an absorption spectrum, when individual atoms absorb discrete colors of light. Kirchhoff's Laws summarize the statements about these spectra:
Refer to Figure 4-18 in your textbook for a picture of Kirchoff's laws in action. What is the physical basis for these laws? Emission of light occurs in atoms at specific wavelengths due to the nature of the atomic structure (the electrons in orbit). So if one had a big dense star composed entirely of hydrogen, why don't you just see the hydrogen lines? There are lots of ways that the photons can interact in a dense gas to change their wavelengths (scattering for example). All these complicated interactions (including the emission of light from free electrons interacting with the hydrogen nuclei) produce photons with all sorts of wavelengths. Hence a continuum (thermal or blackbody) spectrum is produced. If the gas is rarefied, then the photon emitted from an individual atom will be able to escape from the gas without being altered and you will see the appropriate emission lines (Law 2). The gas needs to be kept warm so there will be a source of energy to permit the emission of light. The temperature required depends on the emission lines that are going to be produced. Higher energy photons require higher temperatures. So a thin hydrogen cloud heated by a nearby star will produce hydrogen emission lines, but a hydrogen cloud that is cold, sitting alone in interstellar space, will not produce those lines. Law 3 is a bit harder to understand at first. Why does looking at a continuum source through a cloud of gas produce an absorption spectrum? Photons from the continuum source go into the cloud and the atoms absorb precisely those photons that match up with their atomic energy levels. But that same gas also emits light at those energy levels so shouldn't it all end up making no difference? The difference is that the emission photons are reradiated out in all directions, not just back into your line of sight. The net effect, therefore, is the removal of most of the photons at the absorption line energies from the light which is traveling along your line of sight. Hence, the absorption spectrum.
In the case of the sun, one sees the continuum spectrum coming from the solar surface, or photosphere, with absorption lines produced by gas in the surrounding solar atmosphere. If one looks off the face of the sun at the gas in the surrounding hot corona, the extended atmosphere of the sun, one can see emission lines from hot thin gas.
Thus it is that by observing emission and absorption spectra an astronomer can determine the chemical composition of clouds of gas in space. Other things besides atoms have specific absorption and emission properties. For example, molecules, which consist of atoms bound together (such as water which is two hydrogens bound to an oxygen) have energy levels which can emit and absorb specific wavelengths of light. The situation is analogous to the atom but a bit more complicated. The emission (absorption) lines can be closely packed together yielding emission (absorption) bands. Water molecules have an absorption band in the microwave region and this is exploited by the microwave oven. Microwave photons are absorbed by the water causing the water to increase its energy level (heating it).
If we look at the spectrum of the sun we find emission and absorption lines caused by the presence of specific elements. The strength of a given line depends on several factors: the amount of the element, the temperature and pressure of the gas, atomic physics, and the possible presence of magnetic or electric fields. The types of lines that atoms give off under a particular set of circumstances can be determined to a large extent by experiments in the laboratory. Then when we see those lines in the sun we learn something about the sun's composition. We have learned from spectral data that the sun consists of about 76% Hydrogen (H), 22% Helium (He) and 2% everything else. This is fairly typical for the universe as a whole. As an interesting historical sidenote, Helium was first discovered as unknown emission spectral lines in the sun's corona.
We have discussed now how light can permit one to measure the temperature of stars and planets and learn of their compositions. One can also measure motion toward or away from us by using the doppler shift. If an object is approaching you, the light waves are "crunched up" a bit, i.e., the wavelength of the light is reduced which means that the light is shifted towards the blue. If the source of light is moving away from you then the wavelength of the light is stretched out, i.e., the light is shifted towards the red. These effects, individually called the blueshift, and the redshift are together known as doppler shifts. The shift in the wavelength is given by a simple formula
(Observed wavelength - Rest wavelength)/(Rest wavelength) = (v/c)
Put another way, this just states that the percent change is equal to the velocity of the emitter as a fraction of the speed of light. The rest wavelength is what you would observe from an object at rest with respect to you, and v is the velocity of the object emitting the shifted light. Note that the velocity is positive (away from you) if the shifted wavelength is longer than the original rest wavelength. A note of caution: this formula is appropriate only for velocities significantly less than the speed of light. There is another formula for speeds close to the speed of light, but we won't be using it in this course. The effect (i.e., redshift or blueshift) is qualitatively the same even at these high speeds however. Also note that the speed determined by the doppler shift is only the radial velocity that is the velocity toward or away from you. Transverse motions do not produce a doppler shift in this way. Thus the doppler shift only gives us part of the motion of a given star, namely that motion towards us or away from us. Motion across the sky can only be determined with slow, painstaking observations over very long periods of time (this is called the proper motion of a star).
In the case of the sun, its surface is boiling and seething, and the
sun itself is pulsing from energy produced in its interior. The
velocities of these motions can be directly measured using doppler
shifts. Since the frequency of these pulses, and the way they appear on
the surface depend on the properties of the gas in the solar interior,
careful doppler studies allow us to probe into the interior structure
of the sun.
In this section we will be considering the Sun as a prototypical star. We will be most concerned with understanding the basic properties of the Sun, its interior structure, how astronomers have learned about the Sun. We will not be focusing on how the Sun interacts with the solar system, its effect on the Earth, etc.
Here are some learning goals for the study of the Sun:
Here are some review questions on the Sun:
 In this course, Astronomy
124, we will be learning about
the contents of the universe, from the relatively small scales of a
single star system up to the largest distances known, namely the entire
visible universe. Along the way we will encounter various types of
galaxies, clusters of galaxies, clusters of stars, interstellar gas and
dust, neutron stars and black holes, and, of course, individual stars.
The stars, in fact, are a very basic constituent of the universe so it
is important to get a good grasp on the properties of them. The most
familiar of all the stars is our Sun. Many of the properties of the Sun
will be common to all stars, so we will begin with it.
In this course, Astronomy
124, we will be learning about
the contents of the universe, from the relatively small scales of a
single star system up to the largest distances known, namely the entire
visible universe. Along the way we will encounter various types of
galaxies, clusters of galaxies, clusters of stars, interstellar gas and
dust, neutron stars and black holes, and, of course, individual stars.
The stars, in fact, are a very basic constituent of the universe so it
is important to get a good grasp on the properties of them. The most
familiar of all the stars is our Sun. Many of the properties of the Sun
will be common to all stars, so we will begin with it.
What are the most obvious properties of the Sun? It's hot and bright. A slightly more subtle point was recognized by ancient astronomers who determined that the Sun moves through the sky on a daily and annual cycles, and that these cycles account for the length of the day and the seasons of the year. Many ancient structures and monuments (for example, Stonehenge) are believed to be designed to keep track of these sky motions. With the coming of the Renaissance and the work of Copernicus, Galileo, and Kepler it was realized that the observed motions of the Sun were not a property of the Sun itself, but of the rotation of the Earth and its orbital motion around the Sun. So what are we left with? It's hot and gives off light. Let's try to learn something more.
What is there to know about the Sun? How about its size, mass, composition, internal structure, temperature, source of its heat and light, age, and life history? Pause for a moment and reflect upon the general issue of how one would set about to learn these things. You can't travel to the Sun. You can't get pieces of it to examine. All you can do is observe it, and perform experiments on Earth to help you learn about the laws of nature. With a little thought you might be able to relate the results of your physics experiments back to what you are observing in the heavens. This is the way it is with astronomy.
We begin with a rather straightforward property of the Sun, namely its size and the distance to it. Note, however, that determining even something as simple as the size of the Sun is not so straightforward. You can see the Sun but just how far away is it? If you know the distance to the Sun then the apparent size of the Sun directly gives you its diameter. Alternately if you knew how big the Sun was you would know how far away it was. But you know neither. In astronomy it is customary to express the apparent size of something in terms of the angle that the Sun's image takes up on the sky. (Apparent size is just how big something looks; it is an observed quantity, not an intrinsic property. The task of the astronomer is to move from what is observed, that is how things appear to us, to the general property, how things really are.)
What are the units of angle? Recall that the total angular measure around a circle is 360 degrees. The angle from (say) the eastern to western horizon (through the point directly overhead, the zenith) is 180 degrees. The Sun, as it turns out, has an apparent diameter of about 32 arc minutes (a minute is equal to 1/60th of a degree; a second of an arc is equal to 1/60th of a minute). Another unit of angle is the radian which is the angle that gives an arc of a circle equal to the radius. The advantage of using the radian as the unit of measure is that you can convert directly from angular size to a relationship between size of the object and the distance to it: Specifically, the diameter of an object divided by the distance to it is equal to its apparent size in radians.
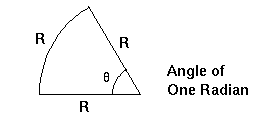 FIGURE:
Units of angular measure. The radian is a unit of measure which gives
an arc on a circle equal to the radius of the circle. It is about 57.3
degrees in size.
FIGURE:
Units of angular measure. The radian is a unit of measure which gives
an arc on a circle equal to the radius of the circle. It is about 57.3
degrees in size.
Now, given that, one can use the rules of trigonometry to determine the diameter of the Sun if one knows the distance, or one could determine the distance if one knew the diameter. But how does one determine a distance? In the case of the Sun it was done in the same manner that we determine distances here on the Earth: by the method of triangulation. It is of some historical interest to note that the size of the solar system was first measured by observing the planet Venus crossing over the face of the Sun (in 1761 and 1769) from several locations on the Earth and triangulating to obtain the distance from the Earth to Venus. (The observing expedition to Tahiti was led by Captain James Cook.) Anyway, the average distance from the Earth to the Sun is 150,000,000 kilometers (1.5 × 108). The angular diameter of the Sun is 32 arc minutes which is equal to about .009 radians of angle which means that the Sun is about 1.4 × 107 kilometers in diameter (about 110 times that of the Earth). Since in astronomy we most often refer to the radius of stars and planets, and we use the units of centimeters (cm), we shall note that the radius of the Sun is 7 × 1010 cm.
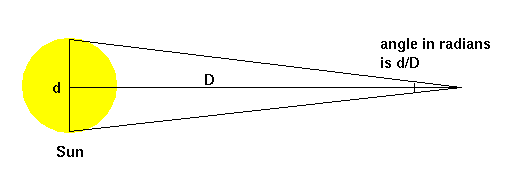 FIGURE: The diameter of the Sun and its distance
away from us are related by the apparent angular size of the Sun. The
ratio of the diameter to the distance is equal to the size of the angle
in radians.
FIGURE: The diameter of the Sun and its distance
away from us are related by the apparent angular size of the Sun. The
ratio of the diameter to the distance is equal to the size of the angle
in radians.
Next consider the Sun's mass. Historically it was a major advancement to realize that there was such a property as mass and what it meant to have a certain mass. On Earth we think of mass as the amount of "stuff" something has, or how much it "weighs." Obviously we can't take the Sun and put it on a balance as we might do if we were measuring the mass of some rock. What other properties does mass have? Newton is the scientist credited with the major discovery that mass implies a gravitational attraction between objects with mass, that is, they exert a pulling force on each other. Newton worked this out quantitatively and he determined the mathematical relationship
Fgravity = G M m / R2
describes the force of gravity between two objects of mass M and m and separated by a distance R (the term G is a constant that relates the units of mass and distance to those of force). Note that Newton's Law of gravity tells us that the gravitational force between two objects rapidly becomes weaker as those objects become further apart. It also tells us that the force of gravity is stronger in direct proportion to the mass M.
Hence we measure the Sun's mass by its gravity. The Earth is maintained in its orbit around the Sun by the gravitational attraction of the Sun. Newton discovered that if there are two bodies with mass m1 and m2 orbiting each other, then the size of the orbit (given by a) is related to the period of the orbit (specified as P) by the following formula:
P2 G (m1+m2) = 4 pi2 a3
The general relationship that the orbital period squared is proportional to the orbital radius cubed is originally due to Kepler and is known as Kepler's Third law. Throughout this semester we will be concerned with determining the mass of things, from other stars, to black holes, to whole galaxies and even the whole universe. The only way we have to measure mass of such objects is through the gravitational force that they exert on other objects. (Note: this material is covered in more depth in Astronomy 121, and is discussed in Chapter 2 of your text. We introduce it here simply to show you how the mass of the Sun can be determined, and by extension the mass of stars in orbiting binary star systems. Indeed, forms of this law allow us to estimate the masses of entire galaxies. So this is an important concept although we must leave out the more extensive discussion of Newton's laws which would permit a more thorough understanding of the derivation of Kepler's law.)
Using Kepler's law, the period of the Earth's orbit (1 year), the size of the orbit (the distance to the Sun given above) and a value for the constant G in the equation permits us to obtain, through simple algebraic manipulation, the value of m1 + m2, the combined mass of the Earth and the Sun. This will be very nearly equal to the mass of the Sun since the mass of the Earth is completely insignificant. (If you were weighing an elephant by more or less conventional means then the presence of a few dust specks on his back would hardly throw the measurement off by a significant amount.) As it turns out the mass of the Sun is just about 2 × 1033 grams (gm). For comparison, you weigh about 5 × 104 gm.
(The mass of the Earth can be similarly determined by the orbits of satellites around it, or, more simply from the acceleration due to gravity at the Earth's surface. What was not known for a long time was the value of the constant of proportionality in Newton's law, namely G. This was determined by Henry Cavendish in the 1790s by measuring the attractive force between two objects of known mass. As you should imagine, this required a very sensitive experiment because the force of gravity is very weak--G is very small. This experiment has sometimes been referred to as "weighing the Earth" but it might better be referred to as "weighing the universe" because it was the final key piece needed to use Kepler's orbital equation to determine the masses of the Earth, the Sun, indeed the whole universe.)
Given the mass of the Sun and its size we can compute its density. The density of something is equal to its mass divided by its volume. Specifically, for a sphere we have
rho = M / ( 4/3 pi R3)
where the Greek rho is our symbol for density and the R is the radius of the sphere. If you plug in the numbers for the Sun you get a density of 1.4 gm/cm3. For comparison, water has a density of 1 gm cm3, and rock around 3. So the average density of the Sun is not all that different from you. (You are about equal to water as evidenced by the fact that the human body is nearly neutrally buoyant in water; you float but not well enough to keep your nose out of the water. Does it surprise you that the Sun is about as dense as water? Did you think it might be denser because it's big, or less dense because it's floating in space? Beware of casual thinking and naive expectations in astronomy!)
Now let's return to the properties of the Sun that we first mentioned: heat and light. Why is the Sun giving off heat and light? The answer for the ancients was in terms of a familiar phenomenon: the Sun must be on fire. A more appropriate analogy for today's more sophisticated student might be the filament of a light bulb (so long as you don't conclude that the Sun is powered by electricity.) The point is that you already have experienced the fact that sufficiently hot things give off visible light. The Sun, like all stars, is just a hot ball of gas that is giving off blackbody radiation. Let's examine how the Sun is hot and why.
Visible Parts of the Sun
When we look at the Sun the surface that we see is called the photosphere. We can only see down into the Sun until the opacity is large enough to scatter the light. The deeper that one looks the higher the temperature. This accounts for the phenomenon known as limb darkening, which refers to the fact that the Sun appears darker out on its edge. This is because out at the edge you have to look through a thicker layer of solar atmosphere (because you are looking slantwise through it) when compared with the center of the Sun. You see mainly the higher layers of the photosphere where the temperature is lower, at about 4000K. At the center you are looking deep into the photosphere and the temperature is higher and consequently the Sun appears much brighter. (The same sort of thing happens when you look at the stars in the sky; stars overhead are less obscured than stars on the horizon because the stars on the horizon have had to pass through a greater column of the Earth's atmosphere and so are subjected to more scattering of their light.)
The surface of the Sun has a mottled appearance called "granulation." This represents the upper end of the convection cells that are in the outer layers of the Sun. Convection is a process by which heat is transported from hot to cool regions through the physical motion of the gas. Here the convection cells are places where hot gas boils up from deeper within the Sun. The center of a granual, or convection cell, is where the rising hot gas is. Since the gas has higher temperature it is brighter than the region surrounding the cell where cool gas is sinking.
Another sort of mottling that one can see in the Sun are the sunspots. Sunspots appear dark because they are at a much lower temperature than the surrounding photosphere, specifically about 1500K cooler. Recall that the energy flux in a blackbody goes like temperature to the fourth power, so a small change in temperature amounts to a substantial reduction in the emitted flux or brightness. Hence sunspots are dark. Sunspots are believed to be caused by powerful magnetic fields poking up through the Sun's surface. Sunspots follow something known as the solar cycle so that there are periods of maximum sunspot activity every 11 years. The causes of the sunspot cycle are not well understood.
Above the photosphere lies a region called the chromosphere. It has this name because this layer of the Sun's atmosphere can be seen during the last moments before totality in a solar eclipse as a pinkish layer (hence color, or chromo). The pink is due to the red emission line of hydrogen (the so-called "Balmer" line). The chromosphere is about 2000 km thick. Although it has a lower density than the photosphere, the chromosphere has a higher temperature. Indeed from the base to the top of the chromosphere the temperature increases to about 100,000 degrees. The chromosphere also features spike-like jets of gas called spicules that can stick up as much as 10,000 km above the photosphere.
Finally the outermost layer of the Sun is the corona, a region of diffuse glowing gas which can only be seen from Earth when the much brighter glare from the Sun is blocked by a solar eclipse. (The corona can be studied all the time by satellites in space through the use of an obscuring disk to block out the Sun and make an artificial eclipse.) The corona extends for as much as a million km around the Sun and has temperatures as high as two million degrees. In fact some regions of the corona are sufficiently hot that they give off X-rays. The corona interacts with many of the more dynamic aspects of the solar atmosphere. Examples include prominences, which are great arcs of gas that extend outwards from the Sun, and solar flares which are great explosions and jets of gas from the solar surface. All these contribute to solar activity which is tied in somehow with the sunspot cycle.
The Solar Interior
The only visible layers of the Sun are the photosphere and the solar atmosphere. How is it possible for astronomers to develop an understanding for the nature of the interior of the Sun? They do it by using the known laws of physics and the limited amount of information that we have measured directly from the Sun, namely its mass, radius, composition, surface temperature, and luminosity.
Two more observations help us with our effort to model the Sun. The first is that the Sun appears to have a constant radius; it is neither expanding nor contracting. Since the Sun is a ball of hot gas wouldn't you expect it to expand outward into space? Yes, if there were no other force acting on that gas. The other force is the force of gravity which is pulling the gas together. The Sun is in a state of balance between the pressure forces of the gas and the gravitational force due to the Sun's mass. This balance is called hydrostatic equilibrium. Now pressure is a force per unit area; you exert pressure on a wall if you put your hand on it and push. That pressure force is exerted only over the surface area covered by your hand. Pressure produces a net force, which in turn means a net acceleration (from Newton's laws of motion) only if it is not in balance with some other force. Isometric exercises are an example of force per unit area in balance. Another example is provided by differences in water or air pressure. At great depths the pressure of water would crush a scuba diver's lungs if they contained only the air pressure corresponding to the surface. Scuba gear provides air at the same pressure as the surrounding water, which allows one to breathe. The force of the interior air pressure plus the forces exerted by the walls of the lungs are in balance with the sea water pressure. There is no net force on the lungs. Now back to the Sun. Gravity is pulling the mass of the Sun downward. In order for pressure to counterbalance that force the pressure at the center of the Sun must be very large and decreasing as one goes outward through the Sun. So the concept of hydrostatic equilibrium allows us to predict immediately that the Sun has a high pressure center.
The next fact that we will use is that the Sun is radiating away a great deal of luminosity but remains at a constant temperature and constant luminosity. Since energy is flowing out from the Sun and it is not cooling off, energy must be generated somewhere inside the Sun. Since the Sun is not heating up that energy generation rate must be equal to the Sun's luminosity. This is the concept of thermal equilibrium.
The source of the Sun's energy was a mystery for many years. Evidence found on the Earth suggested (what was then regarded as) a tremendously old age for the Earth. Fossil algae and bacteria were dated at ages in excess of a billion years. This meant that the Sun must have been burning much as it is today for at least as long. If the Sun were burning by chemical reactions it wouldn't last more than a few thousand years. The most reasonable (incorrect) answer was that the Sun's luminosity came from gravitational contraction. If the Sun were slightly out of balance so that gravity was pulling it into a smaller and smaller ball, then the gas composing of the Sun would be compressed to ever increasing densities. When you compress a gas it heats up. For the Sun that heat could radiate away as the Sun's luminosity. However, the entire energy available from such a gravitational energy would power the Sun for only 30 million years. This is a lot longer than chemical reactions but still too short for the age of the Earth.
The correct answer was arrived at in the twentieth century. The first step was the development of Einstein's theory of relativity which showed the equivalence of mass and energy (as generally stated in his famous equation E=mc2). Given this equivalence one can then imagine that it might be possible to convert mass directly to energy (through some means). For example, given that the mass of the Sun is 2 x 1033 grams and the speed of light is 3 × 1010 cm/sec, then we find that the equivalent energy for the entire mass of the Sun is 1.8 × 1054 ergs (= gm (cm/sec)2). Since the Sun's luminosity is 4 × 1033 ergs/sec this gives a possible lifetime of 4.5 × 1020 sec, which is 14 thousand billion years. This at least allows the possibility of having a Sun as old as the Earth!
In fact the Sun is not converting all its mass directly into energy. The only known mechanism to convert mass completely into energy is through matter/antimatter annihilation and this is ruled out because the Sun is composed entirely of matter. Instead the Sun uses the mechanism of nuclear fusion wherein atoms of a light element (in this case hydrogen) are joined together to form a heavier element (helium). In the Sun the predominate energy generation mechanism is the fusion of four hydrogen atoms into one helium atom. In this process a small amount of the total mass (0.7%) is converted into energy.
 The process of nuclear fusion is related to but
different from the process of nuclear fission
wherein large atoms are broken apart and the resulting pieces have less
mass than the original atom. Nuclear fission occurs (for example) when
uranium atoms split apart. Nuclear fission powers nuclear reactors and
atom bombs. Controlled nuclear fusion reactors do not exist at this
time although they remain the subject of considerable research.
Uncontrolled nuclear fusion reactors do exist: they are called H-bombs,
or thermonuclear weapons. To give you some idea of the power of E=mc2
if we consider your basic 10 megaton nuclear explosion (pictured), the
energy given off (10 megatons) represents the energy found in 47 grams
of matter (about one and a two thirds ounces). This would be produced
through the fusion of just under 7 kilograms of hydrogen.
The process of nuclear fusion is related to but
different from the process of nuclear fission
wherein large atoms are broken apart and the resulting pieces have less
mass than the original atom. Nuclear fission occurs (for example) when
uranium atoms split apart. Nuclear fission powers nuclear reactors and
atom bombs. Controlled nuclear fusion reactors do not exist at this
time although they remain the subject of considerable research.
Uncontrolled nuclear fusion reactors do exist: they are called H-bombs,
or thermonuclear weapons. To give you some idea of the power of E=mc2
if we consider your basic 10 megaton nuclear explosion (pictured), the
energy given off (10 megatons) represents the energy found in 47 grams
of matter (about one and a two thirds ounces). This would be produced
through the fusion of just under 7 kilograms of hydrogen.
Although it would perhaps be better if humanity left fusion to the Sun, considerable research into it has been done (as you might suspect), and this has coincidentally led to a better understanding of the interior of the Sun and other stars. The main point is that in order to force atoms to fuse into new atoms one needs to overcome the electrical forces of the nucleus. Atomic nuclei have positive charges from the protons in them and since like charges repel each other, it is difficult to force two protons together. Doing so requires considerable energy, that is high temperatures. On Earth in order to get H-bombs to work one has to set off an A-bomb to generate the millions of degrees of temperature necessary for fusion (such A-bombs are euphemistically known as "triggers.") In the Sun, such temperatures come naturally but only at the Sun's core. Hence we expect that the energy generation process in the Sun takes place only in its very center. The temperatures in the center of the Sun are in excess of 10 million degrees and the densities go as high as 160 gm/cc.
The fusion process that the Sun uses is known as hydrogen burning by the proton-proton chain because it depends on a reaction that combines two protons into one deuterium atom. One proton is the nucleus of a hydrogen atom. A deuterium atom is "heavy hydrogen" which is composed of one proton and one neutron. The reaction is
1H + 1H ---> 2H + e+ + neutrino
where the symbols stand for Hydrogen with one proton (1H), hydrogen with a proton and a neutron (2H), also known as deuterium, a positron (e+) which is the positively charged antimatter form of an electron, and a neutrino. This reaction proceeds at a rather slow pace; it depends on turning a proton into a neutron and this is a reaction with a very slow rate (it involves the so-called weak nuclear force). The positron annihilates with an electron producing some energy, and the neutrino escapes from the Sun with no further interaction. Neutrinos have a very difficult time interacting with anything so in the Sun the neutrinos generated by nuclear reactions represent an energy loss. Anyway, as the deuterium atoms are produced they can react with protons (ordinary hydrogen) to produce helium 3 which is two protons and one neutron, thusly
1H + 2H ---> 3He + gamma ray
Energy is carried off by the gamma ray photon. When enough Helium 3 atoms have accumulated they can combine to form one Helium 4 (which is what we regard as ordinary Helium) plus two protons (hydrogen)
3He + 3He ---> 4He + 1H + 1H
The net reaction is four hydrogens turn into one Helium plus a two positrons, two neutrinos, and some energy in the form of two gamma rays and high speed motion in the reaction products. Later on in our study of stars we will discuss other types of nuclear fusion.
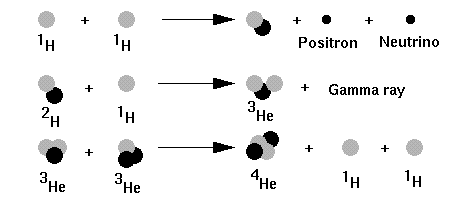 FIGURE: The proton-proton chain illustrated.
Protons are grey spheres, neutrons black spheres, the positron and
neutrion labeled little black spheres.
FIGURE: The proton-proton chain illustrated.
Protons are grey spheres, neutrons black spheres, the positron and
neutrion labeled little black spheres.
The energy released by these nuclear reactions must make its way out through the Sun from the core to the surface through the process known generically as energy transport. Everyone is instictively aware of this process in terms of heat flowing from hot things to cold things. Specifically this means that energy is moving from regions of high energy to regions of low energy, and temperature is a measure of the average energy. There are three main processes by which energy is transported: Conduction, Convection and Radiation. Let's consider radiation transport first. Radiation transport is heat transport by photons (light). We discussed this briefly when we mentioned that a blackbody at a higher temperature than its surroundings would send out photons to those surroundings and eventually cool down to a temperature equal to the surroundings (if not continually supplied with new heat from some energy source). Radiant heat is the heat you feel coming off from a glowing fire, or the heat you feel while standing in the Sun. In both cases you are absorbing photons coming to you from a source at high temperature. (Note: to protect yourself from radiant heating, you should surround yourself with nonabsorbing, i.e., reflective material. Fire protection suits are made of shiny reflective material.) In the Sun photons are produced in great abundance in the core. These photons then diffuse outward from the center of the Sun to the surface where they escape into space. The photons do not simply stream outward. They are scattered by the dense gas in the Sun and so must work their way outward by a series of random scatterings. The scattering is mostly off of electrons in the gas that have been stripped off of the atoms by the high temperature (an ionized gas known as a plasma). This "resistance" to the free travel of photons through the gas is called opacity, as in opaque. The higher the opacity of the material, the harder it is for light to move through it. (Example: dry air has a very low opacity, and light travels a long way through it before being scattered. Hence you can see a long way through the air. Air containing water droplets, i.e. fog, has a much larger opacity. Light is scattered after a relatively short distance. Imagine the interior of the Sun like a bright, hot, dense fog of plasma.) It takes about 100,000 years for photons to work their way out from the center of the Sun to the surface.
Another heat transport mechanism is conduction. In conduction heat is carried not by photons but by other particles, most often by fast moving electrons. Suppose you have a lump of hot material which has electrons jiggling very rapidly about within that material. You place it next to a cold lump which has slow moving electrons. The fast moving electrons at the interface between these two materials collide with some of colder slow moving material and this collision exchanges energy. The cold material starts to move faster and the hot material a little slower. The electron collisions are trying to even things out. You will be familiar with conduction as a heat transport mechanism because it is what makes some material hard to touch when hot and other materials easy to touch. As you know, metals heat up fast and transmit heat fast. This is because they have lots of electrons that can move easily about within the metal. This is the same reason that the conduct electricity well. Conductors of electricity will also conduct heat. Similarly electrical insulators are often good heat insulators. You may have copper cooking pans but the handles are composed of insulating plastic. Even if a good insulating material is at high temperature you can handle it briefly because the rate of heat exchange between you and that material is very slow. This, by the way, is the secret to walking on glowing coals with your bare feet. But woe unto anyone who walks on glowing metal. Anyway it turns out that the Sun is not a particularly good conductor of heat, at least compared to radiative transport by photons. It is a general rule that things will always use the most efficient and fastest mechanism to transport heat in an attempt to come into temperature equilibrium. So in stars, so long as radiative transport is more efficient than conduction, conduction effects will be negligible. There is a certain class of star where conduction is important but we will delay that discussion until later.
The last major heat transport mechanism is convection. Convection is the physical transport of heat by moving large blobs of hot material from the hot region to the cold region. (If you carry a bucket of hot water along you are physically transporting heat.) In a star convection occurs whenever there is a tendency for hot material to rise and cold material to sink. What is required is that the hot gas is less dense than the cold material and so weighs less than the cold gas. This produces an overturning and circulation in the gas. A good example is the hot air balloon. If you heat the air in a hot air balloon then that air will be less dense than the cold surrounding air that the balloon has displayed. The balloon will be buoyant and will rise up through the atmosphere. This is a particular manifestation of the general rule for the atmosphere that most people are familiar with: hot air rises and cold air sinks. Another example is the phenomenon of boiling water. The hot water at the bottom of the pot rises up to the top and the cold water sinks. In this way heat from the bottom of the pot is transported rapidly up to the top of the pot. Convection is a very efficient means of heat transport. Think how rapidly boiling stops if you remove a pot from the stove (its source of heat).
In the Sun convection is also an important process. Convection becomes important whenever the opacity goes up and the rate of radiative diffusion becomes less. Then heat builds up and the boiling begins. Radiative diffusion is most important in the inner 80% of the Sun, convection in the outer 20%.
All the concepts we have been discussing can be expressed in terms of mathematical equations. Collectively these are known as the equations of stellar structure. These include: (1) The force balance equation for hydrostatic equilibrium. In this equation the gas pressure forces, which are determined by the density and temperature of the gas, are in balance with the gravitational force whose magnitude is determined by the amount of mass inside the star. (2) Energy conservation equation which simply says that the luminosity of the star must be equal to the amount of energy being generated inside the star. Energy generation is determined by the nuclear reactions inside the star and these in turn depend upon the composition (how much hydrogen versus helium for example), the temperature (needs to be high) and the density (also needs to be high). (3) The energy transport equation which says how rapidly energy (heat) can be transported through the star at any one moment. As we have discussed, the rate of energy transport depends on such things as the gas opacity which in turn depends on density and pressure. (4) Mass conservation equation: when you have calculated your way to the surface of the star you had better have a total mass that is equal to the mass of the star. In the case of the Sun this is one solar mass Mo.
Given these equations the astronomer programs a computer and then works towards a solution to the each of the equations subject to the condition that the solar model must have the same luminosity, mass, radius, and surface temperature as the Sun (it wouldn't be a very good model otherwise). The outcome is data giving the temperature, density, pressure, luminosity, etc. at every radius throughout the Sun. Solar models tell us that the Sun generates almost all of its energy in its core, the inner 20% of its radius. Most of the mass is contained in the inner 60% of the radius. The upper 20% consists of the convective zone which serves to transport the inner heat out to the surface of the Sun.
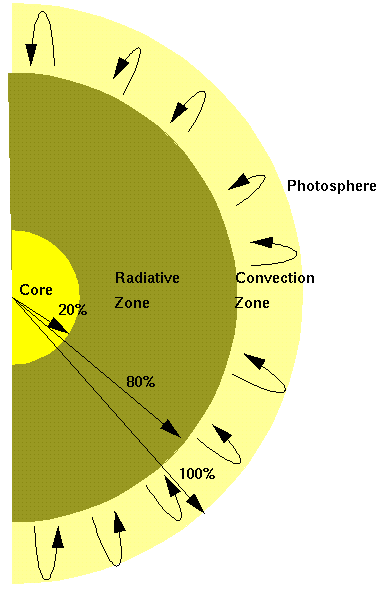 FIGURE: A cross-section of the
Sun. The major sections are the core, where nuclear reactions occur,
the radiative transport zone and the convective zone. The convective
zone reaches out to the photosphere where the photons finally escape
and fly out into space. The photosphere is what we see as the surface
of the Sun.
FIGURE: A cross-section of the
Sun. The major sections are the core, where nuclear reactions occur,
the radiative transport zone and the convective zone. The convective
zone reaches out to the photosphere where the photons finally escape
and fly out into space. The photosphere is what we see as the surface
of the Sun.
Just how certain are astronomers as to the accuracy of their solar models? There are many things that need to be understood accurately in order to get a good model. The biggest challenges are: (1) accurate nuclear reaction rates: how fast do the energy-generating nuclear reactions take place given a certain density, temperature and composition? (2) accurate opacities: how do photons interact with gas at a certain temperature and density? (3) How does convection work in detail? How can you accurately describe regions of hot, overturning, boiling gas? How fast does it transport energy? How fast does it mix? Obviously if you get some of this wrong you can get a wrong model. For example suppose you find that nuclear reactions occur a little faster than you previously thought. This means that you could get the same energy generation from a smaller temperature and density in the core of the Sun. But if the density and temperature are smaller then the size and mass of the solar model would have to change too. The model might have the same mass as the Sun but a larger radius perhaps. Or perhaps it would have the same radius but a more condensed core with a larger percentage of the solar radius in the low pressure, low density convective envelope. We will later be talking about a whole variety of stars that have different masses, luminosities, radii, and internal structures. For all these different stars models have been developed to understand their interiors and their evolution.
Must we solely rely on models to gain understanding of the center of the Sun? As mentioned earlier there is no way to look into the center of the Sun using light. But the neutrinos that are released by the nuclear reactions in the Sun pass right through the Sun and emerge immediately. This is because neutrinos have a very hard time interacting with anything so they stream through matter as if it weren't there. If we could nevertheless detect some of those neutrinos we would be detecting something from the very heart of the Sun. However, the same property that allows the neutrinos to escape from the Sun means that they are very difficult to detect (detecting something means that you made it interact with something to produce a measurable response).
The solar neutrino experiment of astronomer Ray Davis is based upon the fact that neutrinos can interact with a chlorine atom to become an argon atom. The odds of that interaction occurring are very small but if you have a large number of chlorine atoms and a huge number of neutrinos passing through then you might expect to get an event every now and then. The experiment consists of a 100,000 gallon tank of cleaning fluid (which contains chlorine) in a mine in South Dakota. The tank is down in the mine to help shield it from cosmic rays. The mile of rock overhead doesn't represent an obstacle for the neutrinos. From the solar models and the expected rate for the neutrino-chlorine interaction we can predict that the tank will see one argon atom produced every day. About every month the tank is purged of its argon and the total amount of argon is measured. Notice that this is not an easy experiment. We are talking about extracting something like 30 atoms of argon from 100,000 gallons of cleaning fluid. Despite the difficulties neutrinos have been detected over the experiments long run (it has been going since the late 60's). However, the number of neutrinos detected is only one-third the amount predicted. What does this mean? Could there be problems with the equations of stellar structure, or the values of the nuclear reaction rates? Is there something about neutrinos that we don't understand? Are the Sun's nuclear reactions reduced for some reason? Is there new physics we haven't included in our models?
Additional clues are expected from the operation of new neutrino
detectors. These are based not on chlorine but on the element gallium
and are considerably more sensitive than the chlorine experiment which
is only able to detect the most energetic neutrinos. However,
preliminary results are more or less consistent with Davis's result,
namely that there are fewer neutrinos detected than expected from the
theoretical calculations. At the present time physicists believe the
most probably explanation lies in the properties of the neutrinos
rather than those of the Sun. However, the experiments continue to
operate and in the next few years astronomers hope that the situation
will be further clarified.
We now begin to apply some of the things we have learned so far in this course to the study of stars. The understanding of light that we have developed will allow us to classify and characterize stars according to such properties as temperature, brightness, spectral lines, and luminosity. These properties can, in turn, be compared to the Sun as our standard star.
Here are some learning goals for the study of the Stars:
Here are some review questions on Stars:

Photometry
Luminosity, as we have already discussed, is the energy given off per unit time by a star. The concept of brightness is energy per unit time per area. We would like to know a star's intrinsic luminosity, but all we can measure directly is its apparent brightness.
To see the difference between luminosity and brightness, imagine one of those old time street lamps that consists of a large frosted globe. At the center of that globe there is a small lightbulb but you can't see it directly because of the globe. The globe itself gives off plenty of light but the globe itself is not particularly bright. However, if you remove the globe and look at the small filament at the center of the bulb, it appears very bright. The total amount of energy per second is the same (and all coming from the bulb) at 100 Watts. But the brightness depends on how big the surface is that is radiating the light. The same thing is true for the frosted lightbulbs you have at home. You can look at such a bulb directly, since it isn't too intensely bright, but in a bulb with clear glass the filament inside is too bright to look at directly.
Brightness is the energy emitted per time per area. The filament of a lightbulb has some large brightness (it has a very small surface area). When you look at the filament, its image is focused onto your retina in your eye and that image contains the full painful brightness of the filament. As you back away from the bulb the area of your retina that is affected becomes smaller as the apparent size of the bulb shrinks. But the smaller area in your retina will still be hit by light of the same brightness. (This is why looking at the sun is always dangerous. It is intensely bright and the image of the sun on the retina will damage the retina. This is especially dangerous during a partial eclipse only because the total light is sufficiently reduced that you could look at the sun without being overwhelmed. But any bit of the sun that still pokes around the face of the eclipsing moon will still be as bright, and hence as damaging to the portion of the retina upon which the light falls.)
Light bulb frosting shields your eye from the filament and reduces the brightness of any part of the bulb to a lower level, but without reducing the total light given off, i.e., the luminosity. What is happening is that a certain amount of energy is given off by the filament (per second) and that energy spreads out through space. The further out you are in space the less energy per unit area there will be. The frosted bulb intercepts the light and spreads it out uniformly at a lower brightness. Similarly, this explains why a single light bulb will effectively light a small room but not a very big one. The amount of light hitting the walls per unit area in a big room will be very small. This effect of the energy spreading out over space is known as the inverse square law, because the apparent brightness drops off as the inverse distance squared from the light source.
 Figure: The inverse square law for light. As
the light from a
source spreads out, filling an every increasing volume of space, the
energy per unit area (brightness) drops of as the area of a sphere,
that is brightness goes as one over the radius squared,
1/r2.
Figure: The inverse square law for light. As
the light from a
source spreads out, filling an every increasing volume of space, the
energy per unit area (brightness) drops of as the area of a sphere,
that is brightness goes as one over the radius squared,
1/r2.
The system of measurement used by astronomers for brightness is somewhat perverse. It it based on the historical stellar brightness measurements of the ancient Greek astronomer Hipparchus. He called the brightest stars first magnitude stars, the ones he felt to be half as bright second magnitude, and so forth down to the faintest visible stars which were sixth magnitude. Notice that this means that magnitudes go backward, i.e., brighter stars have lower numbers. In this way the magnitude system is like golf scores at a major tournament: the lower the number the brighter the star. Hipparchus's system was based upon the response of the observing instrument, namely the human eye. It just so happens that the eye's response is not linear but more logarithmic, hence the magnitude system is a logarithmic scale. In the modern system, 5 magnitudes is defined to be a factor of 100 in brightness, so as to be relatively close to the ancient definition of magnitude.
The brightness of a star as we see it in the heavens is known as its apparent magnitude. The apparent magnitude of a given star is what we would measure with a telescope. This is not an intrinsic property of a star, however since the apparent magnitude depends on how close a star is to Earth, hardly a universal property. For the intrinsic brightness of a star the astronomer works in terms of the absolute magnitude which is the brightness that a star has at a standardized distance of 10 parsecs. Now if one knows the intrinsic or absolute magnitude of a star, then the difference between that and the observed apparent magnitude will tell you how far away that star is. The equation that relates these two magnitudes can be derived from the inverse square law. The quantity (m-M) is referred to the distance modulus because it relates directly to the distance to a star. If a star has a distance modulus of m-M = 0 then it is exactly 10 pc away because the apparent and absolute magnitudes are equal. A positive value of the distance modulus means the apparent magnitude is larger than the absolute, i.e., the star is fainter than it would appear at a distance of 10 pc.
The measurement of magnitudes is called photometry. In principle, photometry is straightforward. One simply measures the amount of light energy captured by a telescope aimed at a star. In practice it can be rather tricky. One needs to know precisely the properties of the telescopes optics: How much light is blocked by the telescope structure, how efficient are the mirrors (or lenses), how good is the detector? Also, the atmosphere absorbs or scatters some light from the star, reducing the amount that can be measured at the telescope. The atmospheric effects depend upon how high the star is above the horizon, altitude of the telescope (thickness of the air), moisture in the air, etc. These sorts of effects can be accounted for in part through the use of standard stars against which the subject star is compared. In addition, these effects are wavelength dependent. For example, some wavelengths of the electromagnetic spectrum are unable to pass through the Earth's atmosphere rendering impossible any ground based observing at those frequencies. Blue light is scattered more by air molecules than red light. The amount of scattering depends on how high the star is above the horizon. An example you are familiar with is the red appearance of the sun when it is low on the horizon; most of the higher frequency light is preferentially scattered away.
Obviously, therefore, one can measure only a small fraction of the complete spectrum of light that a star is producing. Because, in general, astronomers measure only a portion of the wavelength spectrum when they do photometry, they must estimate the amount of light contained in the rest of the spectrum. For example, you will remember from the discussion of blackbody radiation that if you know part of a blackbody curve, you know the whole thing. So a measurement in one part of the spectrum, say, yellow light, allows you to compute what the total luminosity is based on the blackbody curve. Astronomers define a concept called bolometric magnitude which is the magnitude a star would have if all of its light throughout the entire spectrum is included. One must have a bolometric magnitude in order to know the luminosity of a star (that is the total energy per second that it emits).
As mentioned, a ground-based telescope cannot measure the brightness in the entire electromagnetic spectrum. What one does instead is measure a well defined segment of that spectrum. This should be done in a standard way so that other astronomers can make identical measurements at other telescopes. To do this astronomers have created a set of special filters that pass light only within certain wavelength regions. One of the most common set of photometric filters are known as the UBV filters. These are so-called "broad-band" filters because they are transparent to a relatively broad range of light wavelengths. The initials UBV stand for Ultraviolet, Blue and Visual because those frequencies correspond approximately to those regions of the spectrum.
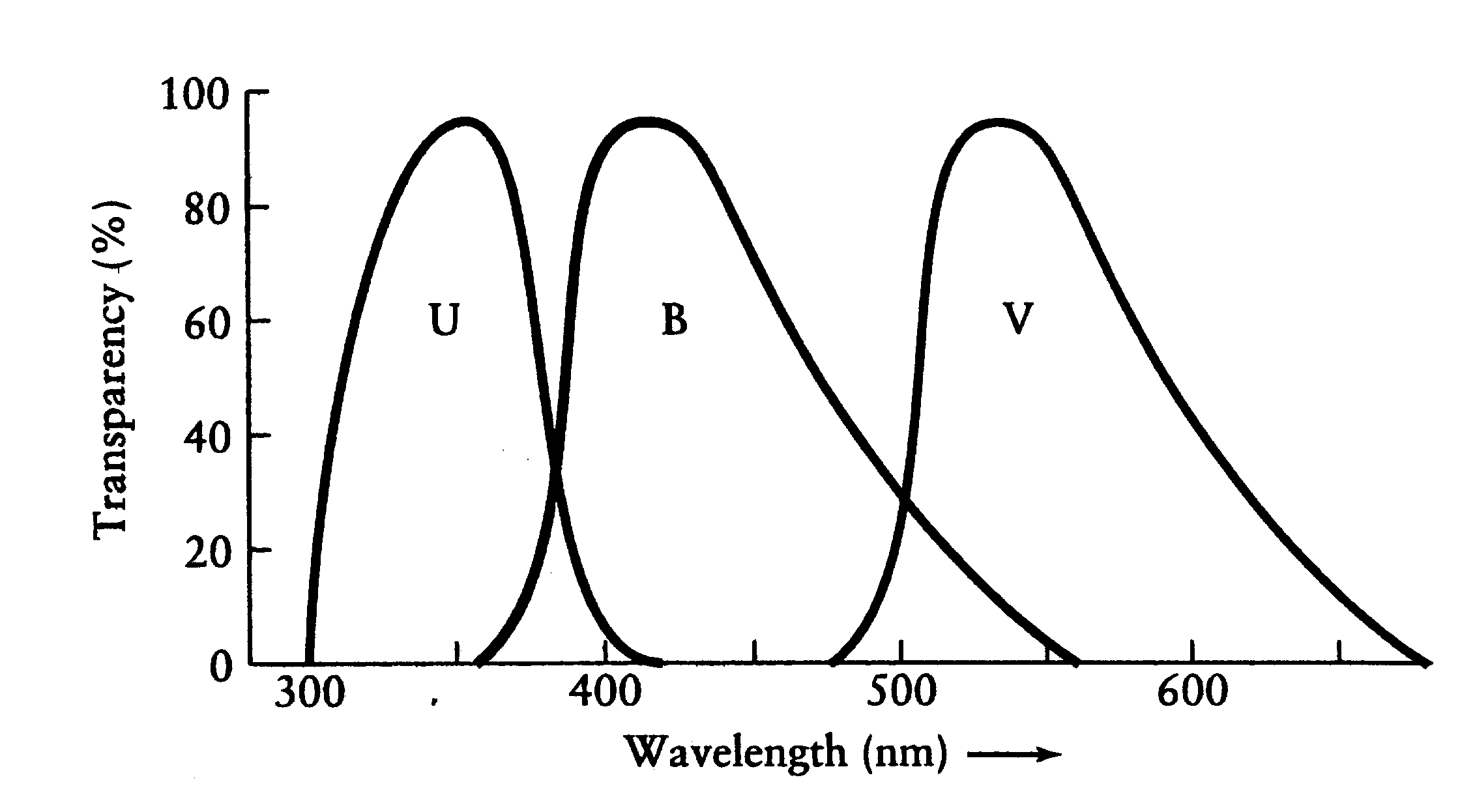 Figure: The approximate spectral range
for the UBV filters. Red light is
700 nm and violet is 400. Hence the V bandpass is centered in the
middle of the visual range, the B is centered on blue, and U is short
of violet, that is in the near ultraviolet. These filters provide
good spectral coverage for the region of the electromagnetic spectrum
that gets through the Earth's atmosphere most easily.
Figure: The approximate spectral range
for the UBV filters. Red light is
700 nm and violet is 400. Hence the V bandpass is centered in the
middle of the visual range, the B is centered on blue, and U is short
of violet, that is in the near ultraviolet. These filters provide
good spectral coverage for the region of the electromagnetic spectrum
that gets through the Earth's atmosphere most easily.
The UBV magnitude numbers give one a concise and standardized way to characterize the brightness and the color (and hence temperature) of a star. Color Indicies are the numbers obtained by subtracting one UBV magnitude from another, say (B-V) or (U-B). Such a number would tell you if the star was emitting more radiation in (say) the Blue band as opposed to the Visual. This would mean that that star is hotter (from the rules for blackbody radiation). But recall also that smaller numbers mean greater brightness in the magnitude system. So a star that had more light in the blue band than in the visual band would have a B-V color index that was less than zero (B less than V). In general, remember that if the color index is negative, the star is brighter in the first of the listed wavebands. If the color index is positive it is brighter in the second of the two. As an example, we have already discussed how the Sun peaks in the yellow-green part of the spectrum so its Visual magnitude is greater than its Blue or Ultraviolet. In fact (B-V) for the sun is +0.62, i.e., it is brighter in V than in B. A star with a smaller B-V would be hotter than the sun; a star with a larger B-V would be cooler. Color indices provide a good way of quickly determining the temperature of a star. We should note that stars are not perfect blackbodies, so astronomers do have to be a bit more exacting, but we will not concern ourselves with those details in this class.
Spectroscopy
Photometry is the measure of the total intensity of light in a certain band of the spectrum. Another astronomical technique is spectroscopy which is the study of the detailed features of a stellar spectrum. To do spectroscopy one must spread the incoming light out into its individual wavelengths. The prisim is an example of a way to do this that everyone will be familiar with. In fact, the first systematic study of stellar spectrum was done by putting a prism at the front end of the telescope (the "Objective Prism Technique"). This spreads out the stellar images so that instead of points of light on the photographic plate one has a line of light, i.e., a spectrum. One can then study the various absorption lines that appear superposed over the continuum. A system of classification was developed, initially using the strength of the Hydrogen "Balmer" lines (see Figures 4-16 and 4-17). In addition to those produced by hydrogen, there are other prominent absorption lines. It was finally realized that the types of lines seen in a star was an indication of the star's temperature. Thus we have the system of spectral type (or spectral class): stars with different spectral types have temperatures and produce different absorption lines.
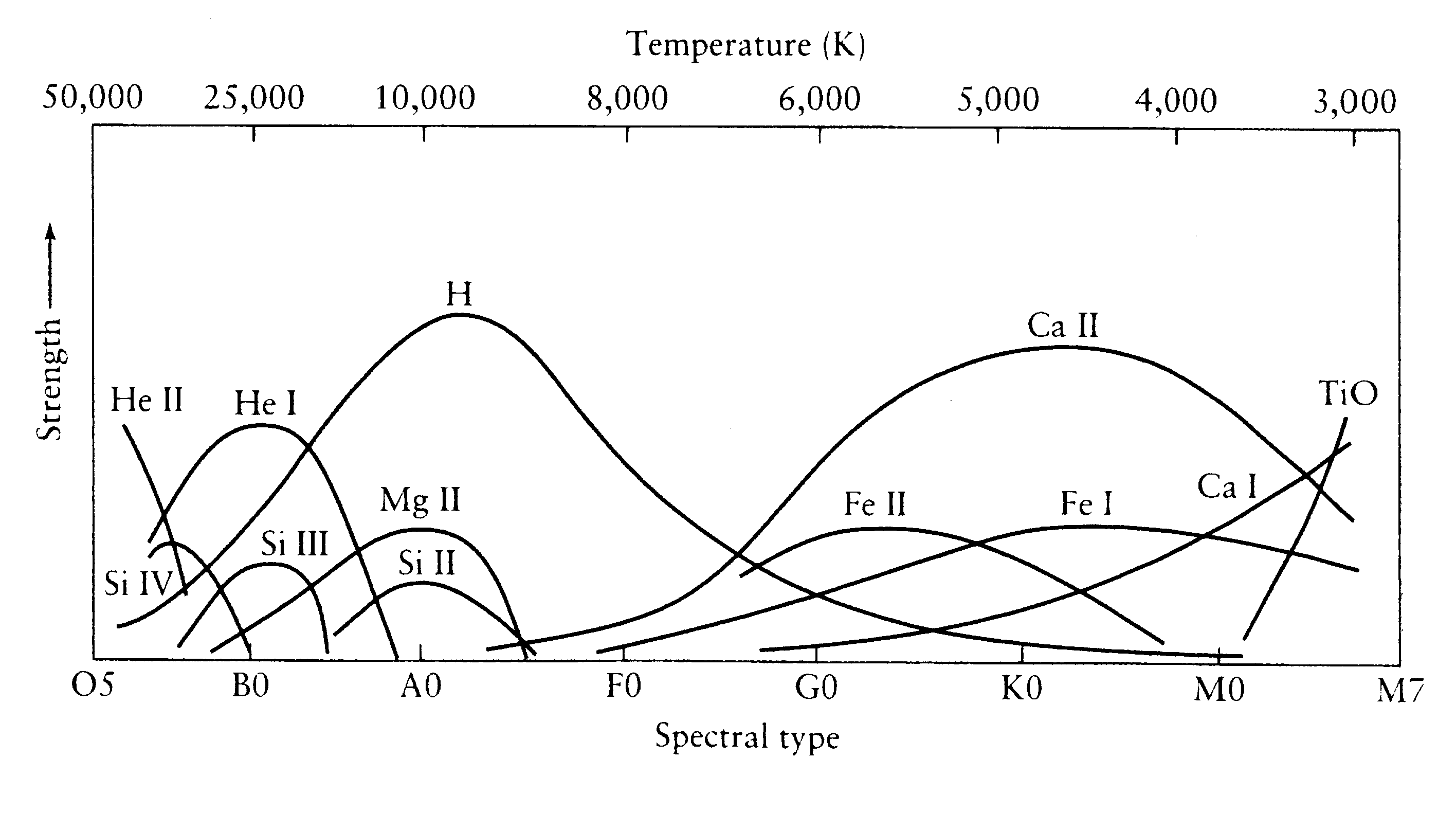
Figure: Figure 16.5 in the book shows relative line strengths
for various types of absorption lines as a function of Spectral type.
Thus it is possible to obtain a star's surface temperature from the
type of absorption lines seen in its spectrum.
The reason temperatures affect absorption lines is not too difficult to understand in a general way. Absorption lines are produced when an electron of an atom is moved from one orbital shell to another one of higher energy through the absorption of a photon. The energies of the electron orbits are fixed by the properties of the atom, and only photons of specific energy (corresponding to the energy difference between those two orbits) can move an electron between two specific orbits. Some types of atoms such as neutral metals (and also molecules) have lots of closely spaced orbits that respond to relatively low energy photons. In the figure above, these are Calcium (Ca) and Iron (Fe). Others such as hydrogen (H) require much higher energy photons. The energy of a photon is proportional to the frequency, i.e., the higher the frequency the higher the energy. At higher temperatures the continuum radiation emitted from a thermal source is shifted to higher and higher frequencies. In other words, hot stars have enough high energy photons to produce the necessary electron jumps to get absorptions in Helium (He) or Hydrogen. Cool stars lack photons of sufficient energy and content themselves with knocking about the molecules and neutral metals. Conversely the hot star's photons are too energetic for neutral metals and molecules (such as Titanium Oxide TiO). They break the molecules apart and completely ionize the metals, that is they strip away all of the electrons. Thus each temperature of star has its own characteristic set of absorption features.
The spectral types most in use today are designated by the letters OBAFGKM; these types are given in order of decreasing temperature, i.e., O stars have the highest temperature, M stars the lowest. The types are further subdivided into 10 subclasses designated by numerals 9 through 0. So for example the sun is a type G2 star. (Here's my own way of remembering the spectral types, from the coolest to the hottest: Mentioning Kepler's Great Finds, Astronomers Bore Others.)
Example: From hotter to cooler: ... A8, A9, F0, F1, F2, F3, ....
Stellar Velocities
The doppler shift gives us the velocity of a star toward or away from us, i.e., the radial motion. Motion perpendicular to our line of sight is known as the proper motion of a star. The proper motion can be determined by careful measurement of stellar positions over a long period of time. We are used to thinking of the stars as fixed, and the constellations unchanging. But the stars are moving. It is just that there motions are generally so small as to be undetectable by the eye in a human lifetime. Telescopes can measure very small changes in stellar positions and hence determine proper motions for many stars (again only the relatively close stars or the fastest moving stars). Radial velocities can be measured immediately and to high accuracy for any star through the use of doppler shifts (as previously discussed). Only if one can get both the radial and proper motion of a star then one knows its true velocity.
In summary, we have learned how astronomers measure the brightness of stars, and how they determine their surface temperatures using both color indices and spectral class. The doppler shift in the spectral lines gives a star's radial velocity, but only a painstaking process of long term observation can give the proper motion and complete the measurement of the star's true velocity relative to the Earth.
We have seen how we can obtain absolute magnitudes of stars (which relates to their total luminosity), and their spectral class (which relates to temperature). We are now in a position to discuss one of the most important diagrams in astronomy, namely the Hertzsprung-Russell or H-R diagram. If you plot the absolute magnitude versus the spectral class you get an H-R diagram. You could also plot the logarithm of the luminosity versus the logarithm of the temperature and get the same graph. The difference is that absolute magnitude and spectral class are the observed quantities whereas luminosity and temperature are derived from the data. The diagram is named for Ejnar Hertzsprung and Henry Norris Russell who independently constructed such a plot. They found that it was not completely filled by the stars. Instead the stars congregated in certain areas and made a long line across the plot. This indicates that there are physical relationships between the energy production rate (luminosity), size (radius) and surface temperature in stars, dictated by the laws of physics.
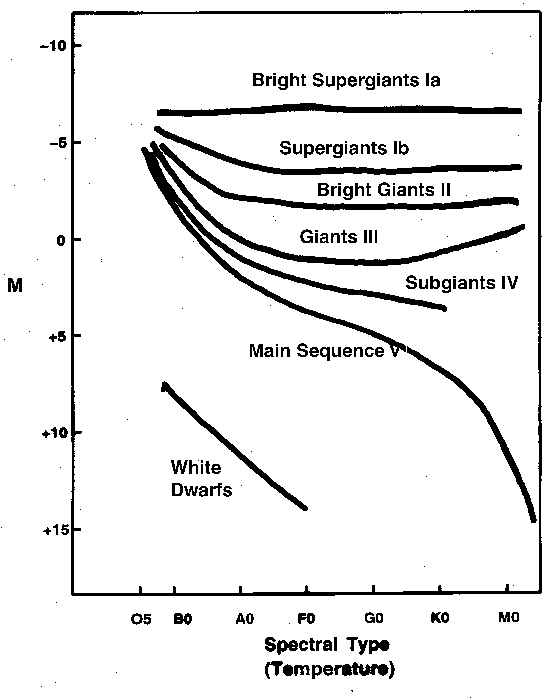
Figure: The H-R diagram is depicted at left and
in Figures 17-14 and 17-15.
Luminosity (or Absolute Magnitude)
runs vertically from low luminosity at the bottom to high at the top.
Spectral class (or temperature) runs horizontally, high temperature to
the left, low to the right. The regions for distinct types of stars
are indicated. These include main sequence stars, giants,
supergiants, and white dwarfs. Spectral class (or color
indices) and magnitudes are the quantities that are observed.
Luminosity and surface temperature are the quantities derived from the
observations. Note that the plot is a log-log plot. That is, the
axes are the logarithm of luminosity and the logarithm of
temperature.
The long line that stretches from the upper left down to the lower right (high luminosity and high temperature down to low luminosity and low temperature) is known as the main sequence. These stars are the stars that are burning hydrogen in their cores. This is the main part of a star's life (neither in the process of being born, nor in its "old age.") The sun is a main sequence star. Across the top of the diagram lie the supergiants. These are relatively rare, huge and luminous stars. Note that the key to understanding the size of stars in this diagram lies with the Stefan-Boltzmann Law and the equation:
L = 4 pi R2 sigma T4.
If a star has a large luminosity then either T or R must be large. If T is small (as it is on the right hand side of the diagram) then R must be huge indeed. Conversely there are stars lying in the lower left hand corner. These stars have low luminosity but they are very hot. By the same equation then they must have very small radii. They are called White Dwarf stars: white because of their high temperature, dwarf for their size. In the upper right hand corner below the supergiants lie the giants, the cooler of them known as red giants (spectral classes K and M).
Binary Stars
When we think of stars, we tend to think of isolated single stars alone in space. However, over half of the visible stars are members of binary or multiple star systems. If the stars in a binary system are widely separated then it is not a bad approximation to consider them separately, as if they are isolated stars. However in many binary systems, the stellar evolution can follow new and different paths. Further, multiple star systems are the only systems where we can use Kepler's laws of orbital motion to obtain stellar masses, an important piece of information.
First, what sort of multiple star systems are there? Multiple star systems occur wherever stars are bound together by mutual gravitational attraction. The most common example is the binary star system in which two stars orbit about each other. Multiple star systems entail hierarchical orbital configurations. In a triple system, for example, a third star orbits a tight binary, A quadruple system would have two close binaries orbiting each other and so on. Basically multiple star systems are built as binaries of binaries and so forth. Other orbital configurations are unstable and would not last.
Multiple star systems are fairly common, so they must be easily formed during the star formation process. In the last stages of protostellar collapse, the cloud out of which a solar system is forming can fragment into multiple pieces that are gravitationally bound together in orbits. Each piece goes on to form an individual star. For example, if the planet Jupiter had been a bit more massive it would have turned into a low mass star and our sun would be a binary. It is also possible that very rapidly rotating protostars may fission into two separate pieces that then form a pair of stars in a very close orbit.
What are the different types of binary systems? First there are the visual binaries so called because we can actually see two separate stars when we look through the telescope. Sirius is an example. The bright star called Sirius is actually two stars: an A1 main sequence star (Sirius A) and a white dwarf companion (Sirius B). For a binary to be a visual binary they must both be bright enough and there must be sufficient separation between the two stars so that they each can be resolved separately in the telescopic image.
In other types of binary systems the presence of the companion star is inferred by indirect means. In astrometric binaries only one star is visible but by following its proper motion one can see that its path "wiggles" across the sky, implying that it is in an orbit with an unseen companion. The center of mass of the binary system would move in a straight line but the star orbits around the center of mass. This would be one way to detect planets for example (since planets do not shine and hence would not be visible).
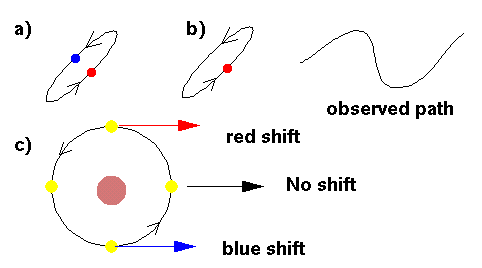 Figure: (a) In a visual binary system one can
see two stars
orbiting each other. (b) In an astrometric binary system one sees only
one star but its proper motion follows a curved path. (c) In a
spectroscopic binary the stars are too close to be seen separately but
changes in doppler shifts reveal the orbits.
Figure: (a) In a visual binary system one can
see two stars
orbiting each other. (b) In an astrometric binary system one sees only
one star but its proper motion follows a curved path. (c) In a
spectroscopic binary the stars are too close to be seen separately but
changes in doppler shifts reveal the orbits.
Not all binaries are visual. There are spectroscopic binaries where the motion of the stars cannot be seen directly but is inferred from the time variable doppler shifts in the absorption lines. For example a hot star of class B or O orbiting with a cool star of class M or K would show helium lines and neutral metals or even molecules, i.e, both spectra would be mixed together. But the two separate spectra would quickly distinguish themselves by their separate doppler shifts. All the lines associated with the hot star would vary as one, and all the lines associated with the cool star would vary as another one. In practice you don't need to have stars of different spectral type, nor do you need to even see the absorption lines from both stars to infer properties of the binary system. The systematic time variation is sufficient.
Perhaps the most interesting of the types of binaries are the eclipsing binaries. These are systems where the light from one star blocks the light from the other at some point in the orbit. This makes the total light from the system seem to vary with time---it is dimmer during eclipse and brighter when the system is out of eclipse. The way that the light changes as a function of time (such a graph of light versus time is known as a "light curve") can give direct information about the size of the stars and the orientation and size of the orbit.
Figure: See Figure 17-10. In an eclipsing binary system changes in the light curve correspond to various points in the binary orbit. The light drops when one or the other of the stars is eclipsed.
There remains one important property of stars that we haven't talked about and that is mass. The problem is that there is no direct way to determine the mass of a star sitting in space in splendid isolation. We need to see something orbiting that star so that we can use Newton's laws and Kepler's third law to derive a mass. Hence the only stars that we can directly obtain masses for are binary stars. All you have to do is determine the period of the orbit and the size of the semi-major axis of the orbit. Recall the formula for this given by:
P2 G (m1+m2) = 4 pi2 a3
If the stars are visual binaries then both stars can be distinguished and followed as they orbit. After mapping out the orbit on the sky, one uses the distance to the system to determine the size of the semi-major axis, and then computes the sum of the stellar masses (m1+m2). If we can determine the center of mass of the system, which is the stationary point about which both stars seem to orbit, then that gives the ratio of the two masses. This allows the individual stellar masses to be determined.
So the long term careful study of binary systems has allowed us to obtain masses for stars. Fortunately, binaries are numerous so many stellar masses have been thus obtained. The most important result of this study has been the determination that for stars along the main sequence there is a direct relationship between the mass of the star and the luminosity, namely that the more massive a star is the more luminous it is as well. Thus we can associate the O spectral class with the most massive stars, and the M spectral class with the least massive. The sun, a G star, is sort of middling in the mass department.
Now what is it about binary stars that affects their evolution when compared to single stars? Stars in a close binary can transfer mass from one star to the other. Since mass is the major determinant in how a star evolves the loss or addition of significant amounts of mass can substantially change the course of a star's life.
To understand close binary systems we have to think about how the stars affect each other. A star influences surrounding things through its gravity. Recall that the gravitational force from an object goes as one over the distance squared. This means that if one were to locate points around a star where the gravitational forces were equal in magnitude those points would all lie on a sphere, that is the gravitational force is "spherically symmetric." Imagine moving two stars together. The gravitational force at any point will be the sum of the gravitational forces of both stars. Now the surfaces of constant force are not spherical, they are distorted into a figure 8 configuration. At some point lying between the two stars the forces from the two stars will be equal in magnitude but opposite in direction. If you move towards one or the other of the stars you will be captured by that star. This point, known as the Lagrange point, is kind of like a low mountain pass between two circularly shaped valleys. Continuing with this analogy imagine the stars to be lakes at the bottom of these valleys. If you were climbing up to that pass and poured out some water you can easily see how the water will flow down to one or the other of the two lakes depending upon which side of the pass you are on. Now imagine one of the lakes having so much water that it completely fills its valley and produces a stream which flows through the pass down into the other lake. In our analogy this is a "water transfer" process.
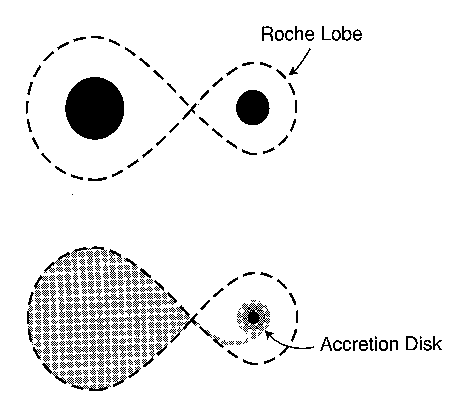 Figure: This figure shows two stars within a detached
binary system, and two stars in a semi-detached binary system
where the gas stream forms an accretion disk.
Figure: This figure shows two stars within a detached
binary system, and two stars in a semi-detached binary system
where the gas stream forms an accretion disk.
In stars it is not water being transferred but gas from the envelope from one of the stars. The transfer generally begins when the star has evolved from a main sequence star up into a giant. The giant star can easily overflow its gravitational basin and dump material onto the other star through the Lagrange point. The figure 8 configuration is known as a Roche lobe so this is often referred to by astronomers as "a star filling its Roche Lobe."
We can classify the state of a binary system by whether or not either of the stars is filling its Roche Lobe. If the two stars are well separated and nowhere near the size of the critical figure 8 surface then they are called a detached binary. If one of the stars is big enough to transfer mass through the Lagrange point then the system is a semidetached binary. If both stars fill their Roche lobes then the system is known as a contact binary. Such a system is almost more like a double-core, figure 8 shaped star.
 Figure: In a semidetached binary system, gas
from one star can
overflow its Roche lobe and fall into a disk orbiting the other star.
This is known as an accretion disk.
Figure: In a semidetached binary system, gas
from one star can
overflow its Roche lobe and fall into a disk orbiting the other star.
This is known as an accretion disk.
Sometimes in a semidetached binary system the mass transferred from one star to another doesn't actually fall directly down onto the compact star but instead goes into orbit around that star. This material forms a disk orbiting around the compact star known as an accretion disk. Gas in an accretion disk can become very hot and glow in visible, UV and X-ray light. Accretion disks can lead to many interesting types of phenomena, particularly when they are located around neutron stars and black holes. Accretion disks will be discussed more detail later.
A Stellar Census
We have now learned that there are hot stars and cold stars, luminous stars and dim stars, stars that lie along the "main sequence" on the HR diagram, stars that are giants, and stars that are dwarfs.
Now let's consider those main-sequence stars. The mass of a star determines most of the properties that that star will have during its lifetime, and the mass determines where a star is on the main sequence. Less massive stars end up at the lower luminosity, cooler end of the main sequence while massive stars end up having high luminosities. Basically the greater gravitational forces of the high mass stars create high temperatures and pressures in their cores which makes the nuclear reactions burn fiercely. Low mass stars, having a smaller burden of mass to hold up against gravity, burn their hydrogen slowly and at a much lower temperature. The smallest stars will be those that have just enough mass to create temperatures and pressures high enough for nuclear reactions to occur at their cores. This minimum mass is estimated to be about 0.08 solar masses.
Along the main sequence mass increases steadily as one goes from the lower right hand corner to the upper left hand corner of the diagram. For main sequence stars there is an approximate relationship known as the mass-luminosity relation that holds. This relationship was derived from the observations of the masses of various types of main sequence stars, but it has also been demonstrated by the calculation of stellar models of main sequence stars. Specifically, a star's luminosity is roughly proportional to its mass to the 3.5 power: L ~ M3.5. Thus a star that is twice as massive as the sun is about 23.5= 11 times as luminous as the sun. The most massive main-sequence stars are about 50 times as massive as the sun. This corresponds to a luminosity almost a million times that of the sun. (Note: the symbol for the sun's luminosity is Lsun, so a million times the luminosity of the sun would be written 106 Lsun.)
Stars spend most of their lifetime as main sequence stars. In general more massive stars do everything faster than low mass stars. They collapse faster, they burn hydrogen faster, they live shorter lives. You might think that a star with a lot of hydrogen would last longer, but no, they squander their resources with abandon. Thus the most massive stars are the most luminous. The lifetime of a star would be given by the total energy available to be radiated into space divided by the rate at which that energy is lost. In other words, amount of fuel divided by rate of fuel usage. In symbols we write tlife ~ Mc2/L where tlife is the symbol we use for the star's lifetime. The Mc2 is of course Einstein's equation for the amount of energy corresponding to mass M. In fact we have already discussed how nuclear fusion releases about 0.7 percent of the total mass-energy. Also in most stars only the hydrogen at the center of the star is available for burning. But the point of this formula is simply to show how lifetime goes like M/L. Now recall the mass-luminosity relationship, L~ M3.5. This means that lifetime goes like 1/M2.5 which is a rapid decrease with increase in mass. For example, the sun has an expected main sequence lifetime of 10 billion years. What is the main sequence lifetime for a star with 10 Msun (i.e. 10 solar masses)? The answer is 1/102.5 times the life of the sun which is about 1/300th which means 30 million years.
Example Problem: Star X is a main sequence star with a luminosity 100 times that of the Sun. What is its approximate main sequence lifetime compared to the Sun?Answer: Using the mass-luminosity relationship, valid for stars along the main sequence, Star X's mass is 1001/3.5 solar masses. This is equal to 3.7 solar masses. Next, its main sequence lifetime is obtained by dividing the mass by luminosity M/L in units of the Sun. This gives an age in terms of the Sun's lifetime, and here we get 0.037 times the main sequence lifetime of the Sun, or 370 million years.
Stars living a main sequence life are all very similar: e.g., they are in hydrostatic equilibrium, they are burning hydrogen into helium in their cores. We have already discussed how the Sun generates energy through the hydrogen fusion. The important thing is that it is using up the hydrogen fuel in its core. This means that the star must evolve and eventually cease to be a main-sequence star. As hydrogen is converted to helium the number of particles in the core drops (4 hydrogen produce one helium). This causes the pressure to drop since pressure depends on the number of particles in a gas. (There are fewer particles bouncing around and colliding with other particles, so the average force exerted by the gas is reduced.) Since the pressure drops, the core must contract; this, in turn, increases the core temperature and reestablishes equilibrium. Increased temperature increases the nuclear reaction rate and increases the luminosity of the star. Note that this process is a very gradual one. For a star like the Sun the luminosity increases about 5 percent per billion years. On the H-R diagram the location of the main sequence star slowly moves upward (increased luminosity) and a bit to the right (lower temperature).
As we shall see a bit later, when we discuss stellar evolution in detail, when stars use up their hydrogen fuel they leave the main sequence region of the HR diagram to become giants and supergiants. Many stars end up their lives as white dwarf stars, in the lower left hand corner of the HR diagram. White dwarf stars are the hot stellar core, left over after all nuclear fusion has ceased. Such stars very gradually cool off, like stellar cinders.
So how many of the different types of stars are there? If one counts the number of stars for each level of luminosity, one obtains something known as the Luminosity Function. One has to be careful to count all the stars within a representative volume of the Galaxy to avoid missing the small, dim stars. Doing this, one finds that most of the stars have low luminosity. This makes sense: first off, low luminosity stars are also low mass stars. Stars form out of interstellar gas clouds, and these will have some amount of initial mass. Given that amount of mass you can make a lot more low mass stars than high mass stars. In fact, there seems to be something in the star formation process that favors smaller massed stars. Second, we have learned that high mass stars live for much shorter periods of time compared to low mass stars. You would expect to find a lot more long-lived stars than short-lived stars.
Of course, when you look into the night sky the stars you see are the brightest stars in the immediate neighborhood. The bright stars are very unrepresentative. A typical star star would be a K or M dwarf, i.e., a small low luminosity red star. On the other hand, the rare high mass star is more interesting; it burns brightly and dies spectacularly, as we shall learn when we take up the subject of stellar evolution.
If the stars are so far away, how do we know their names? - A. Student
Here are some learning goals for the study of Stellar Distance:
Review Questions:
The stars were thought by the ancient astronomer to lie in a fixed sphere that rotated daily through the heavens. The stars were all made part of this one fixed stellar sphere because it seemed that the stars were basically all alike. True, some were brighter than others, but they all moved together in a fixed pattern of unchanging constellations. We know today that the stars do move relative to one another but these motions are impossible to detect with the naked eye over a human lifetime. To understand the true nature of the stars it is necessary to realize how far away they are. However, the estimates made by ancient astronomers of the distance to the stars were all relatively small. The largest known universe of the ancient Greek astronomers, that of Aristarchus, placed the stars out at a distance we would today call a light year. Most of Aristarchus's fellow Greeks regarded his model as too fantastic. The prevailing wisdom of the time placed the entire universe within a sphere roughly of the size that we give to the Earth's orbit around the sun.
It was the invention and use of the telescope that makes it possible for us to analyze the star and know something of their true nature. Galileo first used the telescope to study the stars and discovered that the heavens are filled with many more faint stars than could be seen with the naked eye. Galileo's primitive telescope showed the planets to be small disks; the stars, however, remained unresolved points of light. Nevertheless Galileo's impression was that the heavens were vast and the stars must be at great distances. Since Galileo's time astronomer's telescopes have improved greatly in their ability to capture light, but the stars still remain unresolved points of light even today. Indeed the stars are a long way away.
To the modern astronomer seeking to understand the stars, it is essential to be able to determine accurately distances. This is difficult. The most accurate method we have is known as parallax. It is basically a method of triangulation, and it works only on the closest stars.
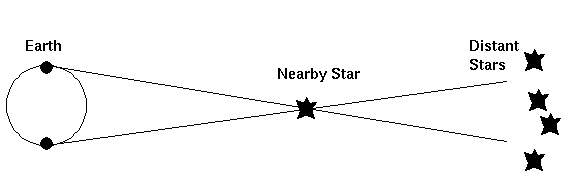
Figure: Stellar parallax occurs as the Earth orbits the Sun
and our line of sight to a nearby star varies. The effect is to make
the star appear to shift position over the course of the year. In
reality, stellar distances are so great that parallax shifts are less
than an arc second, completely unobservable to the unaided eye.
Have you ever thought about why two eyes are better than one? You have two eyes set into your head, separated by a few centimeters. Two eyes allows you to see things in "3D" because each eye views nearby objects from a different angle. The size of that angle decreases for objects at increasing distance, hence your brain is able to take that information and deduce the distances to things. You can demonstrate this by a simple experiment. Hold a finger up about a foot in front of your face. Close one eye and look at the finger. Now open that eye and close the other. The finger seems to jump in position compared to the background. This jumping is simply due to the different direction that each eye looks in order to see the finger. Now increase the distance between your eyes and the finger. At full arms length you will see that the "jump" seen as you switch eyes is much smaller than when the finger is close. The the magnitude of this jump tells you the distance to the finger.
The parallax method works better the more widely spaced your eyes are. That is, the wider the base of the triangle (the "baseline"), the further the distance over which one detects a significant shift. Stars are very far away and we need a big distance between our "eyes" if we are to see any jump. That big distance is given by the orbit of the Earth; observe a star tonight and then six months later when the Earth is on the other side of its orbit. The angular shift you see will give you the distance to the star. For simplicity astronomers have defined a distance term called the parsec. The parsec is the distance that would give one second of arc shift when observed across the baseline of the Earth's orbit. A parsec is equal to 3.26 light years (the distance light travels in one year), also equal to 3 x 1018 cm.
Parallax measures can be obtained only for the nearest stars. The nearest star, Proxima Centari, is at a distance of 1.31 pc, which means that even the nearest star shows a parallax shift of less than one arc second. Parallax measurements can be obtained out to distances of about 20 pc. Almost all the stars you see in the night sky are at greater distances than that. The Hipparcos satellite was designed to get more accurate parallax measurements from space, above the distorting effects of the Earth's atmosphere. Although the mission was not a complete success, it was able to measure parallax angles down to as small as a milliarcsecond.
The careful measurement of stellar positions and the determination of parallax angles is one of the missions of the observatory at the University of Virginia. The telescope located on Observatory Hill (a 26 inch refractor) has been obtaining data since 1885.
In addition to parallax distances the careful measurement of stellar positions allows one to measure the proper motion of stars. The proper motion is defined as the observed motion of the star across the sky (often said as "in the plane of the sky"). This motion is in contrast to radial motion which is the motion directly toward or away from us. We are used to thinking of the stars as fixed, and the constellations unchanging. But the stars are moving. It is just that there motions are generally so small as to be undetectable by the eye in a human lifetime. Telescopes can measure very small changes in stellar positions and hence determine proper motions for many stars (again only the relatively close stars or the fastest moving stars). Radial velocities can be measured immediately and to high accuracy for any star through the use of doppler shifts (as previously discussed). If one can get both the radial and proper motion of a star then one knows its true velocity. Measuring the velocities of the members of a star cluster is one way in which astronomers can determine the distance to nearby clusters. The distance to the Hyades cluster in the constellation of Taurus (the cluster is the "V" at the head of the bull) has been determined through this "moving cluster" method. The Hyades cluster stars serve as important standards for determining the distances to other stars.
The moving cluster method only works for a few clusters that are within about 100 pc of the Earth. How else might we determine distances then? One obvious way to measure distances is to use the brightness of objects whose luminosity is known. You might use this method for determining distances to oncoming cars at night: you judge by the brightness of the headlights. (Actually you probably judge by the apparent size of the distance between the headlights. But what about oncoming motorcycles?) If you knew the luminosity of a star you could measure its brightness and then you would know the distance. Let's review how that works.
An addition to the classification system is to give the stars a luminosity class, which locates the star on the H-R diagram. The luminosity classes are defined spectroscopically by the width of the observed spectral lines. Big stars have lower atmospheric pressure so the atoms in such an atmosphere are not jostled around as much as in a high pressure atmosphere. This means that the spectral lines observed are sharper and narrower. Smaller stars have broader, shallower lines. As it turns out, therefore, a classification in terms of line width actually corresponds roughly to star size. The classifications are given by Roman numerals and are as follows: class I are the supergiants, class II the bright giants, III the giants, IV the subgiants, and V, the most important of all, the main sequence. See Figure 18-9 in the book for the locations in the H-R diagram.
Now, imagine you observe a star. You get its apparent magnitude, its spectral type, and its luminosity class. The spectral type and luminosity class allow you to locate the star on the H-R diagram. You then read off the appropriate absolute magnitude. You now have the distance modulus, hence you can calculate the distance. This technique is known within astronomical circles as spectroscopic parallax because it is a way of finding distance simply by taking a spectrum of a star, although the term is a bit of a misnomer because no parallax is really involved.
Some of the most important data is obtained by studying the H-R diagram for a cluster of stars. All the stars in a cluster are basically at the same distance from us and so all have the same distance modulus. Measuring apparent magnitudes and spectral types place the stars on the H-R diagram. It is through the study of clusters (such as the Hyades) that the H-R diagram is "calibrated" to provide distances to other, more distant, stars.
Obtaining distances from the HR diagram is done by using the diagram to obtain the actual luminosity of a star and then comparing that information to the apparent brightness of the star in the sky. Then, by the inverse-square law of light we know how far the star is from us. Thus, we can determine the distance to anything with a known luminosity. Celestial objects that have known luminosities are referred to as standard candles or, as your book would have it, "standard bulbs". The key point is a light source with a known luminosity (a standard).
An example of a standard candle is any main sequence star. We pretty much know what the luminosity of main sequence stars is. Consider, for example, any main sequence G2 star. This would be a star just like our Sun. The apparent brightness gives the distance right away. A trouble with this type of star as a standard candle is that such stars are not very luminous, so they can't be seen out at large distances. There is a distinct advantage to bright standard candles.
Interestingly enough, one of the best types of star standard candles are certain types of variable stars. Variable stars are stars whose luminosity varies with time as the star pulsates. In particular there is a class of variable star known as Cepheid Variables. The stars vary by about one magnitude over periods ranging from one to 100 days. These variables are located in a certain region of the HR diagram known as the "instability strip." This strip lies up above the main sequence near the red giant region. Stars that are in the instability region of the HR diagram tend to expand and contract as the surface layers heat and cool. What happens is the surface layers start out rather opaque and thus block the escape of radiation. This causes the surface layers to expand outwards. There comes a point where the opacity of the layers drops off and suddenly the light and heat can escape more freely. The outer layers cool off and begin to contract. The whole process is rather like an engine, cycling back and forth: heating, expanding, cooling, contracting. The important observational property of these stars is the relation between their average luminosity and the period of their oscillation: the larger the luminosity the longer the period. This allows the variable star to be used as a standard candle. One simply needs to determine a specific period-luminosity relation for each class of variable star. The Cepheids are higher luminosity variables and they come in two varieties: Type I is the "metal rich" type, meaning they have lots of elements other than hydrogen and helium (to an astronomer everything except hydrogen and helium is called a "metal"), and the Type II or metal poor Cepheids. Type IIs are dimmer than Type Is. Another class of variable star is the low mass red giant type star known as an RR Lyrae variable. These are located at the low luminosity end of the instability strip and they have periods less than a day. RR lyrae stars are good for relatively near by distances. Cepheid variable stars are so luminous that they can be used to get the distances to far away galaxies by using the Hubble Space Telescope.
Here are some learning goals for the study of the Stellar Evolution:
Review Questions:
| Star Name | Spectral Type | Luminosity Class |
|---|---|---|
| Polaris | F8 | I |
| Mirach | M0 | III |
| Rigel Kent | G2 | V |
| Arneb | F0 | I |
| Saiph | B0 | I |
| Shaula | B1 | V |
Before we begin our extensive discussion regarding the evolution of stars, we must start with a discussion of the stuff out of which stars are made, namely the gas and dust that is present throughout the galaxy. This material is collectively known as the interstellar medium: the material between the stars.
One tends to think of outer space as consisting solely of stars separated by great distances with a complete vacuum between them. While it is true that space is mostly empty, there are regions that contain considerable material. This is relative of course. By earthly standards such regions still constitute a pretty good vacuum. For example, the "typical" gas density in space is one atom per cubic centimeter. The best man-made vacuum is about 1012 atoms per cubic centimeter. A cc of the air in the room has about 1019 atoms in it. The interstellar medium is not uniform in density. Although on average its density is one atom per cc, it can have densities up to a thousand or a million atoms per cc.
The interstellar medium is composed of two classes of material: gas and dust. Gas is composed of molecules or atoms of types of gasses, hydrogen being the most abundant. Carbon monoxide, CO, is another common form of gas, as are oxygen and nitrogen. Dust is composed of little bits of solid matter. Dust is very small, on the order of microns (10-6 meters). Dust is made of compounds of carbon and silicon in various forms (graphite grains, silicate grains) and out of ices (such as water, carbon dioxide, ammonia). Temperatures have to be pretty low to have the icy particles (100 K and below). The other kinds of dust and grains can exist at higher temperatures, although if the temperature gets too high all kinds of dust will be destroyed. The composition, nature, structure, etc. of dust particles remains an area of some uncertainty in astronomy.
The interstellar medium manifests itself to the astronomer in various phenomena. The most obvious perhaps are the emission nebula. (Nebula is the latin word for "cloud." Its plural is nebulae.) Emission, you will recall, occurs when a cloud of gas is warmed up by some source of continuum radiation, say from a nearby star. The various atomic energy levels are excited by this radiation, and as the electrons jump back down to their lower energy states they emit photons at distinct spectral wavelengths. Since hydrogen gas is the most common form of gas, hydrogen emission lines are most often observed. In particular, a specific transition in the hydrogen atom corresponds to red light and color pictures of these emission regions appear red. This is the so called H-alpha emission line of hydrogen. It is the same line that made the chromosphere of the sun appear red.
 Figure: The Trifid Neubla
(M20). This nebula exhibits many of the features we are describing
here: the red light comes from hydrogen Balmer emission, excited by the
ultraviolet radiation from a hot star embedded in the nebula. The dark
regions criss crossing the nebula are obscuring dust. The blue region
to the left of the main body is a "reflection nebula" so named because
it consists of dust that is scattering starlight into our line of
sight. Dust scatters short wavelength (blue) light preferentially,
hence the blue appearance.
Figure: The Trifid Neubla
(M20). This nebula exhibits many of the features we are describing
here: the red light comes from hydrogen Balmer emission, excited by the
ultraviolet radiation from a hot star embedded in the nebula. The dark
regions criss crossing the nebula are obscuring dust. The blue region
to the left of the main body is a "reflection nebula" so named because
it consists of dust that is scattering starlight into our line of
sight. Dust scatters short wavelength (blue) light preferentially,
hence the blue appearance.
Emission nebula are also known as HII regions. The explanation of this nomenclature is this: The H means Hydrogen and the Roman numeral II means that the hydrogen is ionized (its electron has been stripped off by high energy photons). H I (H-one) is neutral hydrogen meaning that it still has its electron. He II would be singly ionized helium, and He III would be doubly (fully) ionized helium. These designations become more important for atoms with larger numbers of electrons as it is necessary to keep track of how many electrons an atom has if you are to properly characterize the emission spectrum from that atom.
 If you would like to see an emission nebula,
go out into the night and look at the constellation Orion. One of the
"stars" in Orion's sword will appear to be fuzzy. This is not a star at
all but an emission nebula. If you can get hold of a small telescope or
a good pair of binoculars take a look at it. It will appear to be a
glowing cloud rather than a brilliant point.
If you would like to see an emission nebula,
go out into the night and look at the constellation Orion. One of the
"stars" in Orion's sword will appear to be fuzzy. This is not a star at
all but an emission nebula. If you can get hold of a small telescope or
a good pair of binoculars take a look at it. It will appear to be a
glowing cloud rather than a brilliant point.
The power to keep an emission nebula glowing is provided by hot, high energy stars in the interior of the nebula, specifically O and B type stars. The ionization of hydrogen (and helium which is also seen in an ionized state in the nebulae) requires high energy ultraviolet photons such as will be emitted from stars of those spectral types. The size of the HII region is determined by how many ionizing UV photons there are. Typically a hot O star can ionize hydrogen out to a distance of a few tens of parsecs.
You can do an observing project to see dust. Go out on a dark, moonless night and look at the milky way. The milky way is the disk of the galaxy stretched out like a band across the sky. The stars are so distant and so dense that one sees a diffuse glow rather than individual stars. However, the band is not uniform. There are regions where there is no glow. These areas are dust lanes, places where the dust is sufficiently thick that it blocks the visible light coming from more distant stars. This is an extreme example of interstellar extinction which is the dimming of star light caused by the presence of interstellar material. In the dust lanes the extinction is complete. But in other regions it is only partial. Interstellar extinction will be important in computing absolute magnitudes since it will reduce the apparent magnitude of a star over and above the effect of distance. Extinction is quantified in terms of so many "magnitudes" of extinction, i.e., 5 magnitudes of extinction between us and some other star means that the apparent magnitude we observe will be 5 magnitudes larger than what it would be without the interstellar medium. One tries to correct for this by estimating the extinction and then adjusting the star's magnitude appropriately. The average extinction for interstellar haze is about 2 magnitudes per 10 kpc in distance. Notice that extinction is distance dependent; the more stuff you go through the worse it is. This further complicates matters.
Another way that dust manifests itself is in the reflection nebula. Unlike emission nebula which produce light directly from emission from atoms in the nebula, a reflection nebula merely reflects light from some other source, typically a nearby star. Dust particles can scatter photons of light (think of a photon of light hitting a dust particle and bouncing off). The ability to scatter light depends on the size of the particle and the wavelength of the light. Light photons with wavelengths much bigger than the sizes of the particles are much less affected by the particles than photons with wavelengths comparable in size to the particles. Now the dust in interstellar space has diameters ranging from 0.1--1 micron (10-6 meters). This is 100 to 1000 nm which of course is right in the range of the wavelength of visible light. In practice this means that blue light gets scattered more by the dust than red light. This also explains the blue sky of the Earth by the way. You are seeing blue light preferentially scattered by air molecules (which are very small). Reflection nebula therefore have a bluish appearance. Reflection nebula are often seen close to emission nebula.
This preference for dust to scatter short wavelength light causes another effect known as interstellar reddening. What this means is that there is more light lost from the blue end of the spectrum than from the red end as the light pass through space from the star to you. In practice this means that the U and B apparent magnitudes increase in value faster than the V magnitude. This of course would mess up your calculation of color indices. So again to get accurate photometry one must include a color correction to take into account the effect of reddening. This is expressed in terms of magnitudes in the color indices. A terrestrial example is seen in the highly reddened sun at sunset. The atmosphere is scattering out the blue light leaving the red. If some volcano has sent up lots of fine dust into the air then the reddening becomes even more pronounced. Extinction is a fairly hard thing to measure directly but reddening isn't. By studying the spectrum of a star we get its spectral classification. This gives us a corresponding color index. Comparing this with the observed color index we can deduce the amount of reddening and hence the amount of dust between us and that star. From this we can estimate the total absorption and compute our corrected apparent magnitude.
To summarize the effect of dust: It can absorb photons of light and it can redden a continuum spectrum of light by preferentially scattering out the blue end of the spectrum. The effect of extinction is to increase the apparent magnitude number, that is to decrease the apparent brightness. Reddening increases the color index number, making the star appear redder than it otherwise would.
Example : A star has is a B7 spectral type Luminosity Class V (main sequence). However, its observed color index is (B-V) = +1. What's right or wrong here? A B7 spectral type is a very hot star. From data in the book we know that its temperature should be between 10,000 and 15,000 K, and this corresponds to a black body with a color index (B-V) = -0.1 (see the discussion on page 342). Hence this star is severely reddened. It must also be experiencing considerable extinction.
We have talked about gas and dust, and about how we can detect them through emission and about scattering in HII regions and reflection nebula. There are more types of interstellar regions than just those two type of nebula however. One of these is the cold, dense giant molecular cloud. These clouds are not glowing in visible light, although they are associated with some nearby HII regions. Molecular clouds are detected in the radio frequencies. They mainly contain molecular hydrogen H2, i.e., two hydrogen atoms bound together into an ordinary molecule of hydrogen (NOT to be confused with HII, or ionized hydrogen). What is generally detected however is radio emission from other molecules. The molecules (such as carbon monoxide, hydroxide OH, water, even formaldehyde, ammonia, and alcohol to name just a few) have complex emission spectra associated with their rotational and vibrational states. These are low energy states, hence the photons they emit are in the radio region of the spectrum. Astronomers using radio telescopes have mapped out these great clouds of molecules. Particularly good as a tracer is the carbon monoxide molecule CO. Densities in them range from several hundred to a thousand particles per cc. Temperatures tend to be low, down around 10K.
Hydrogen is the most abundant element in the universe so we should be able to detect lots of it. However, most of it will be at very low temperatures, too low to be ionized or to have many atoms with electrons up in the higher energy orbits. Hence they don't emit any of the visible photons we associate with HII regions. However, radio emission can be detected from neutral hydrogen, or HI regions. This radio emission comes from the difference in energy levels between a proton and its electron (the hydrogen atom) with their "spins" aligned and one where their spins are anti-aligned. (Another way to think of it is as the alignment or antialignment of the intrinsic magnetic N/S axes of the electron and proton.) The point is this: if the electron flips from being aligned to being antialigned it goes from a higher to a lower energy state and emits a photon. The wavelength of that photon is 21 cm. Twenty-one centimeter emission is a very important diagnostic for mapping out the presence of neutral hydrogen in the galaxy, and in other galaxies.
To summarize the states of interstellar gas:
Through our study of the sun we have become aware of what a star is: a hot ball of gas, held together by gravity, generating energy at its core through nuclear reactions, in particular the fusion of hydrogen into helium. We are left with several obvious questions: How did these stars get created in the first place? How long do they live and what happens when they run out of the nuclear fuel that supplies them with energy? These questions fall within the domain of the theory of stellar evolution.
We begin with the subject of star formation. There is much uncertainty about exactly how stars get formed, but we understand much of the general picture. As previously discussed, a star is in a state of hydrostatic equilibrium where gas pressure is balancing the force of gravity. Gas pressure results from the interactions of atoms in the gas; the atoms collide and exert forces on each other. The speed of the atoms is related to the temperature, namely, the higher the temperature the faster the average velocity of the gas particles. So pressure is related to temperature. The higher the temperature, the faster the speed of the particles, the more force they exert on other particles when they collide. For the Sun to be in a state of hydrostatic equilibrium it must be very hot at the center so that the force exerted by the gas can balance the crushing weight of the star's layers above the core.
If the gas were not hot, however, gravity would win. Indeed that is the way that stars form, most likely, out of cold gas that slowly begins to contract due to gravitational forces. Since the gas must be cold and it must be relatively dense for this to happen, we expect star formation to begin within cold (10K) giant moleculars clouds that contain lots of hydrogen (74% ), Helium (25% ), and the more directly observable dust and molecules. Typically these dark nebulae are very massive with enough gas to make many stars.
Note that there are plenty of dark nebulae, HI (neutral hydrogen) regions and giant molecular clouds around that don't seem to be collapsing into stars right now. What triggers the collapse of a cloud to form stars? We are not completely certain but one likely mechanism is the passage of a spiral arm in a spiral galaxy. The spiral arm is believed to be spiral wave (recall the ideas associated with water wave moving across water and sound waves moving through air) that compresses gas as it passes. The compression may be enough to trigger the collapse of clouds into stars. This idea gets some support from the fact that bright young stars are often associated with the spiral patterns in galaxies. A second possible mechanism is the onslaught of a shock wave from a nearby supernova explosion. The shock wave provides the needed compression of the cloud. Compression could also be achieved if two molecular clouds collide. It is likely that all these mechanisms have some role to play. Anything that compresses the molecular clouds could in principle get star formation going.
As the molecular cloud begins to collapse down due to gravity (triggered by whatever means) it fragments into smaller bits. These fragments are known as protostars because they are the bits that will eventually form into stars. As a cloud of gas collapses it is compressed, and as gas is compressed it is heated. The heating stops the process of fragmentation but it is not yet strong enough to stop the contracting protostar.
The protostar "bits" are all destined to become individual stars of assorted mass. Less massive lumps become low mass stars while massive lumps become high mass stars. As a general rule there are lots of low mass stars for every high mass star. This is reasonable since with a given amount of mass you could make lots of little stars or just a few big stars. (Think of a batch of cookie dough and the decision as to whether or not you want to make a few big or a lot of little cookies.) Most of the cloud goes into small mass stars but there are always a few large mass stars created. The distribution of masses is known by astronomers as the Initial Mass Function.
As the gas in a collapsing protostar compresses that gas heats up and begins to glow. The more massive the protostar, the bigger the cloud of gas that is glowing, hence the more luminous the protostar. Collapse continues and the temperature increases further until finally the core of the protostar becomes dense and hot enough for nuclear reactions to begin. Up until this point the heat generated within the protostar could slow its collapse but not halt it. With the activation of nuclear source of energy at its core the protostar can now generate enough pressure to fend off the force of gravity. When nuclear reactions begin the protostar has become a star. The star settles in to begin its life.
The evolution of the forming star can be traced on the H-R diagram. This illustrates one specific use that we can make of the H-R diagram, to show how a star changes during its lifetime. At any given moment a star will have a certain luminosity (L) and temperature (T). This marks a point in the H-R diagram. As a star evolves, its luminosity and temperature may change. As they change we mark new points on the diagram. We can then "connect the dots" to trace out all the temperatures and luminosities that the star had over some period of time. Thus the lifetime of a star can be summarized by an evolutionary track on the H-R diagram. Note that the track alone doesn't tell us how long a star remains at a given temperature and luminosity. That we have to remember or mark on the track with additional annotations.
The specific evolution track followed by a protostar depends on its mass. The general path a protostar follows is from the cold (right hand) side of the diagram toward the hot side (left) as compression increases the protostar's temperature. The protostar is very luminous at first because it is very large and reasonably warm. All protostars continue to contract to smaller size, but the more massive ones heat up sufficiently rapidly to maintain a high luminosity. The less massive stars may decrease in luminosity as they collapse since they remain at lower temperatures but their radius gets smaller (Remember! L ~ R2 T4). In either case the destination in the H-R diagram for stars of all mass is some point along the main sequence. The main sequence corresponds to stars that are in hydrostatic equilibrium and are burning hydrogen in their cores. The point on the main sequence where stars first form lies along the so-called Zero Age Main Sequence (ZAMS).
Figure: Figure 20:11 is an H-R diagram showing how protostars collapse down to the main sequence. The main sequence corresponds to fully formed stars that are burning hydrogen. The mass of the star determines where it lies along the main sequence.
It does not take very long for protostars to complete their collapse to the main sequence, from around 100,000 years for massive stars to a few tens of millions of years for less massive stars. Since stars form out of giant molecular clouds, lots of stars form in a relatively short time. The result is a cluster of stars called an open cluster or galactic cluster. Examples of such clusters include the Hyades and the Pleiades clusters. Studies of such clusters show that many more low mass stars are formed than high mass stars. Once a star begins to burn hydrogen at its center its luminosity can heat up and drive away the remaining gas in its vicinity. When high mass O and B stars are formed their very great luminosity, particularly in UV radiation, is capable of ionizing and heating up extensive regions of gas. This forms HII regions. As previously remarked, these HII regions are associated with star forming regions. Eventually all the hot young stars will completely disperse the star-forming gas leaving behind only the star cluster. In that new cluster you will have lots of stars of different masses (more low mass than high mass stars) all of which were born at about the same time and at about the same distance. As we shall see this makes clusters very good things to study for astronomers interested in learning the life histories of the stars. The stars in a new cluster, if plotted on the H-R diagram, will very nicely trace out the main sequence.
Let's consider how a solar system such as our own forms around the newly-born star. We will do this by thinking about our own solar system as a whole, looking for general facts and trends. What are the implications of those trends for theories of the solar system's formation?
The solar system is mostly empty space and, compared to the Earth, its a very big empty space. To give you some sense of the scale of the solar system we will make a scale model of it using an orange for the Sun. (This is a 1 to 1.4 × 1010 scale model.) If the sun were the size of an orange, the earth would be about 1 millimeter in diameter (and Charlottesville is about the size of a virus on that BB). The Earth would be located 11 meters away from the Sun. The moon is one quarter of a millimeter in diameter and located about an inch from the Earth. Jupiter, the largest of the planets is about 1 centimeter in size and located 60 meters from the Sun. Pluto, the furthest of the planets and the smallest is only a fifth of a millimeter in size and located 430 meters away from the orange Sun. So on the human scale of things the solar system is very big. But the size of our home system pales when compared to the interstellar dimensions. The nearest star (other than the sun), Alpha Centari, is located (on the orange scale) 3000 kilometers away (about the distance to Phoenix).
Our solar system is dominated, not by the planets, but by the Sun. It is located at a distance of 93 million miles from Earth (this distance is referred to as the astronomical unit: 1 A.U. - 1.5 × 1013 cm). While we tend to regard the sun as an extremely significant heavenly body, in the bigger picture the sun is just an average star in a galaxy containing about 100 billion stars. On the scale of the ``orange sun'' the galaxy has a diameter that is about equal to the actual distance to the sun, one AU. We lie out on the edge of our galaxy, a long distance from the center. Viewed from afar our sun hardly rates a second glance.
After the Sun, the next largest bodies in the solar system are the so-called ``gas giant'' planets, Jupiter, Saturn, Uranus and Neptune. Of these Jupiter is the largest and most massive. These planets are composed mainly of hydrogen and helium and they are located in the outer parts of the solar system. Their densities are around 1 gram per cubic centimeter, consistent with their gaseous composition. (Actually 1 gm/cc is the density of water, so on average these planets have the density of liquid, not gas.) They don't have solid surfaces per se, the gas that composes them simply gets denser and hotter as one gets nearer to the center of the planet.
In contrast to the gas giant planets there are the terrestrial planets in the inner part of the solar system, consisting of Mercury, Venus, Earth (and the Moon), and Mars. The terrestrial planets are characterized by higher densities (5.6 gm/cc for the Earth, 3.95 gm/cc for Mars) than the gas giants, meaning that they are composed of denser rock and iron rather than the light gaseous elements. They are all low mass planets compared to the gas giants; indeed their masses, and hence escape velocities, are too small to hold onto hydrogen and helium.
In the outer part of the solar system there are icy bodies that don't fit into either the terrestrial or gas giant planet designation. These are the moons of the gas giant planets which are low density (1-2 gm/cc) icy and rocky bodies with low mass. Pluto is probably this type of world.
Now let's examine some of the overall properties of the solar system:
What sort of picture could explain the formation of the solar system and take into account these interesting facts? The picture that is now widely accepted is that the solar system evolved from a large, slowly rotating cloud of interstellar gas and dust. This cloud was massive enough that it began to collapse due to its own gravity. As it collapsed it did not lose the spin that it had (conservation of angular momentum), so it didn't collapse into a small sphere, it collapsed into a rotating disk. As gravity compressed the gas, it began to heat up. As the disk develops, gas on crossing orbits will collide leading to the formation of mainly circular orbits. The formation of this disk explains solar system facts 1, 2, and 3. Gas in the disk began to spiral down into the center of the disk causing pressure and temperatures to build up there. This was the beginning of the formation of the Sun. We say that the sun began its life when enough mass had built up so that the temperature in the center became high enough to begin nuclear reactions. In order to form the Sun had to lose most of its spin, and it was probably the Sun's magnetic field that ``applied the brakes'' and slowed its rotation. The Sun would thus not be spinning too rapidly, but it would still somewhat share the overall spin of the proto-disk, thus explaining fact 5.
Figure 20.8 shows the collapse of an initially extensive, slowly rotating cloud of gas and dust. The collapse takes place mostly along the direction of the spin axis, until a rotating disk is formed. The sun forms in the center of this disk.
Once the Sun has formed its heat will begin to affect the remaining gas disk. The temperature in the disk will be highest near the Sun and lower as one goes out. This is consistent with the trend (6) in composition for the planets.
The actual process of planet formation is not too well understood, but it probably involves the gradual building up of material that collides and sticks together forming ``planetesimals.'' We believe that the asteroids and the comet nuclei may well be remnant planetesimals. The planetesimals then collide and coalesce to form the planets. Since they all formed out of the disk, these planets would all orbit and spin with the same sense (prograde, facts 3 and 4). A given planet forms by using up all the planetesimals in its vicinity (fact 8). The asteroid belt consists of leftover planetesimals that were never absorbed into any planet (probably because of the mass of Jupiter affecting their orbits). Large planets further out from the Sun also can accrete gas to become the gas giants. Some of the leftover gas may get drawn into a disk spinning around the gas giant, thus forming a miniature solar system as moons form out of this ``mini-disk'' (fact 7).
Some of the initial planetesimals get ejected out beyond the orbit of Pluto to form the nuclei of the comets. The young sun continues to heat things up, and blows excess gas and dust out of the solar system. The remaining planetesimals collide with the newly formed planets causing extensive cratering. Eventually the planetesimals are used up and the cratering dies out to today's low rate. The result is the solar system we see today.
We have considered the formation of stars, and something of their lives as main sequence stars. Now we turn to what happens to a star when it runs out of hydrogen fuel in its core and must end its existence as a main sequence star.
Stars living a main sequence life are all very similar: e.g., they are in hydrostatic equilibrium, they are burning hydrogen into helium in their cores. There is one significant variation to this theme worth mentioning. It has to do with the way massive stars burn hydrogen. We have already discussed how the Sun generates energy through the hydrogen fusion process known as the proton-proton chain. This is the most important fusion process for main sequence stars with mass less than about 1.5 Msun. More massive stars burn hydrogen mainly by an alternate mechanism known as the Carbon cycle, or Carbon--Nitrogen--Oxygen, CNO cycle. Specifically the CNO cycle looks like this:
12C + H ----> 13N + gamma ray
13N ----> 13C + positron + neutrino
13C + H ----> 14N + gamma ray
14N + H ----> 15O + gamma ray
15O ----> 15N + positron + neutrino
15N + H ----> 12C + 4He
The key points about this reaction are (1) the carbon acts like a catalyst, that is it isn't used up in the complete set of reactions. (2) The outputs are the same as in the proton-proton chain, that is you get two positrons, two neutrinos, one Helium and some energy. (3) This series of reactions isn't important in the lower mass stars because it takes more energy to ram a hydrogen onto the carbon; the carbon has a greater electrical charge and hence a larger electrical repulsive force to overcome (than in the proton-proton reaction). The temperature in the core needs to be greater than 15 million K in order for the CNO reactions to become important.
What is important in this description: (1) Understand the meaning of the notation describing nuclear reactions. (2) Remember that nuclear reaction rates are determined by temperature and density. Generally, reactions involving heavier elements require higher temperatures and greater densities. This will be important in the evolution of a star.
Now, regardless of the star's mass or whether it is primarily burning hydrogen via the proton-proton or CNO cycle, the important thing is that it is using up the hydrogen fuel in its core. This means that the star must evolve and eventually cease to be a main-sequence star. As hydrogen is converted to helium the number of particles in the core drops (4 hydrogen produce one helium). This causes the pressure to drop since pressure depends on the number of particles in a gas. (There are fewer particles bouncing around and colliding with other particles, so the average force exerted by the gas is reduced.) Since the pressure drops, the core must contract; this, in turn, increases the core temperature and reestablishes equilibrium. Increased temperature increases the nuclear reaction rate and increases the luminosity of the star. Note that this process is a very gradual one. For a star like the Sun the luminosity increases about 5 percent per billion years. On the H-R diagram the evolutionary tracks of main sequence stars is from the ZAMS line upward (increased luminosity) and a bit to the right (lower temperature).
More serious changes occur when the hydrogen in the stellar core is finally exhausted, leaving behind an inert core composed of helium. The only hydrogen still available for burning is the material surrounding the core (the part of a star surrounding the core is called the envelope of the star). Recall that if heat transport is largely by radiative diffusion the different layers of the star will not mix, as they would if the heat transport mechanism were convection. Hence in such stars, when the core runs out of hydrogen no more hydrogen gets mixed down into the core although the surrounding layers will still have most of their original hydrogen. High temperatures from the core make it possible to burn this hydrogen in a "shell" surrounding the core. During this hydrogen shell burning the envelope of the star expands and cools in response to the greater amount of energy released by the hydrogen burning shell. The star becomes very luminous and very big. The sun, for example, will expand out to a size about equal to the Earth's orbit. As the size increases the temperature of the outer surface of the star drops. (Recall the relationship between luminosity, radius and temperature L ~ R 2 T 4.) Thus, the star becomes a red giant. When plotted on the HR diagram the star would be found up (higher luminosity) and to the right (lower temperature) from the main sequence. This is where the giants (luminosity class III for example) are located. When a star evolves so as to leave the main sequence and become a giant we say it "moves up the red giant branch."
Meanwhile back down in the core of the star the hydrogen is all used up and hydrogen burning can no longer occur. Because there are no more nuclear reactions the core must contract. This contraction is a slow process, but it results in an increase in the core's temperature. The temperature must become very large (100 million degrees) before the next nuclear burning can begin: Helium burning. Helium burning requires much higher temperatures than hydrogen burning because helium nuclei have two protons and hence a greater electrical charge. Thus to force the two helium nuclei to come together and fuse one must overcome a very strong electrical repulsion. The only way to force them together is with the very high energies associated with high temperatures. Helium burning cannot begin until the core shrinks and the temperature rises. But this is not the whole story. Another problem with helium burning is that the product of two heliums is a nucleus of Beryllium (8Be). This is very unstable to falling apart back into a pair of heliums for no net energy release. However, if a third helium hits the Beryllium before it falls apart then it can form a stable carbon nucleus 12C. What we need is a three particle interaction (which is much rarer than a two particle interaction). This is known as the triple-alpha reaction. Helium nuclei are also known as alpha particles, and it takes three of them to form a carbon, hence the name.
4He + 4He ----> 8Be + 4He ---> 12C + gamma ray
Three body reactions are very sensitive to density; you need lots of nuclei packed together to make them work. In the contracting core both the temperature and density are rapidly increasing. Once the temperature and densities in the helium core become large enough the triple alpha reaction can begin and we say that the star has core helium burning.
Exactly how the Helium burning begins depends upon the mass of the star. In stars with mass greater than about 3 Msun the helium burning begins smoothly when the temperature in the core gets to about 108K. In lower mass stars the helium burning begins explosively in the so-called Helium Flash. The difference between the two cases depends on the way that the pressure behaves as a function of density and temperature. Again the key concept is the balance between pressure and gravity. Pressure must increase as the core contracts if pressure is going to come back into balance with gravity. Similarly, if the core expands then pressure would decrease. In most situations the pressure that the gas in a star has is a function of both the density of the gas and its temperature. Increase either the temperature or the density and you increase the pressure. (In a balloon or a basketball the gas pressure provides for the "inflation." You know you can increase the pressure by increasing the number of gas molecules, i.e., pumping in more air. You can also increase the pressure by increasing the temperature. Another common example is the automobile tire. The tire pressure increases when the tire becomes hot.)
The rate at which nuclear reactions take place also depends on temperature and density. Fusion reactions occur when nuclei can be forced together in close proximity. However, the positive charge of the protons creates a repulsive electrical force (like signed charges repel so positively charged nuclei are electrically repelled). So you need high speeds (energies) in the nuclei to overcome this electrical force. Higher speeds of the nucleus are associated with higher temperatures in the gas (higher energy), so increasing the temperature increases the force with which nuclei slam together and hence the likelihood of nuclear reactions occurring. An increase in density is simply an increase in the number of nuclei available to react. The more nuclei the greater number of reactions.
Now one can see the basic picture. Suppose for some reason the star contracts a little. Then the temperature and density will go up and the nuclear reactions will increase, further increasing the temperature and the pressure. If the pressure increases more than needed the core will expand, the temperature drop, and the number of reactions drop. The whole process then becomes "self-correcting" and the star stays in hydrostatic equilibrium. This is what happens during a star's hydrogen burning main sequence lifetime, and for helium burning in stars with the larger mass helium cores. In those stars as the temperatures and densities become large enough that helium burning begins, the pressure comes up to balance the gravitational force leaving the star with a new, stable helium-burning core.
In lower mass stars another effect is important. This a different kind of pressure, known as electron-degeneracy pressure. The details of this kind of pressure depend on quantum mechanics at a level beyond what we can cover in this course. But the basic idea is this: quantum mechanics says that you can't put more than one electron into a given energy state, so as you pack electrons together more and more electrons are forced into high energy states. These high energy electrons exert a pressure. Even if you lowered the temperature of the gas these high energy electrons couldn't go to low energy states because they are already occupied by other electrons. So the pressure doesn't drop when the temperature does. Suffice it to say that when electrons become packed closely enough together they strongly resist further compression. The important aspect of this is that the pressure they exert depends on the density of electrons, but not on the temperature. Heat it up or cool it down and the pressure stays the same. Now for the lower mass stars the core temperatures are lower and the pressure that is supporting the core is due to electron degeneracy. When Helium burning switches on the release of nuclear energy causes the temperature to rise. However, this doesn't change the pressure which is coming mainly from electron degeneracy. So there is no balance achieved and the temperature continues to climb. This leads to an out-of-control nuclear burning known as the Helium Flash. However, because of the runaway nuclear burning the temperature does eventually get large enough that ordinary gas pressure becomes greater than the degeneracy pressure. At this point the core expands and stabilizes. Subsequently, the core burns its helium quietly. The helium flash takes place down in the core of the star and hardly affects the outer layers at all, so it is not directly observable.
After the helium flash one is left with a star in a new equilibrium: a core burning helium into carbon and a surrounding hydrogen-burning shell. Such a star now settles in for a period as a horizontal branch star. The "horizontal branch" is like the main sequence: a distribution of stars on the HR diagram. The main sequence is composed of those stars burning hydrogen in equilibrium whereas the horizontal branch stars are the helium burners.
 Clusters of stars are
groups of stars, held together by their mutual
graviational attraction. Astronomers classify three types of
clusters: globular clusters, open clusters and associations.
The first, the
globular
cluster
are the largest and oldest type of star cluster. Their name comes
from the fact that they have a spherical shape. Globular clusters
contain 10s of thousands up to a million stars. They are found
throughout the galaxy and in orbit around the plane of the disk of the
galaxy.
Clusters of stars are
groups of stars, held together by their mutual
graviational attraction. Astronomers classify three types of
clusters: globular clusters, open clusters and associations.
The first, the
globular
cluster
are the largest and oldest type of star cluster. Their name comes
from the fact that they have a spherical shape. Globular clusters
contain 10s of thousands up to a million stars. They are found
throughout the galaxy and in orbit around the plane of the disk of the
galaxy.
 The
open
cluster represents young
stars, relatively recently formed, and these clusters are located in
the disk of the Milky Way (the location of all recent star formation).
Open clusters typically have 100 to 1000 stars. Such clusters are not
as densely packed as the globulars, and these clusters are not as well
bound together by the mutual gravitational attraction of their stars.
These clusters will eventually disperse throughout the galaxy.
An example of an open cluster is the famous "Seven Sisters"
or Pleiades cluster in the constellation of Taurus.
Associations are less well defined groups of hot young stars found in
regions rich with gas and dust. Associations generally contain a few
to about 50 stars.
The
open
cluster represents young
stars, relatively recently formed, and these clusters are located in
the disk of the Milky Way (the location of all recent star formation).
Open clusters typically have 100 to 1000 stars. Such clusters are not
as densely packed as the globulars, and these clusters are not as well
bound together by the mutual gravitational attraction of their stars.
These clusters will eventually disperse throughout the galaxy.
An example of an open cluster is the famous "Seven Sisters"
or Pleiades cluster in the constellation of Taurus.
Associations are less well defined groups of hot young stars found in
regions rich with gas and dust. Associations generally contain a few
to about 50 stars.
Considering the substantial changes that take place when a star runs out of hydrogen in its core, one can see how it should be easy to distinguish between main sequence stars and red giants and horizontal branch stars. Now consider where this might come in handy. Suppose we observe a stellar cluster. All the stars in that cluster were formed, more or less, at the same time out of the same giant molecular cloud. So all the stars started out on the ZAMS simultaneously. Now the more massive stars will leave the main sequence first, with the less massive stars following at the appropriate time. Since we have a good idea how long it takes stars of the various masses to evolve off the main sequence all we have to do is find out what stars are still on the main sequence and what stars aren't. The spectral type of this main sequence turn-off point gives the approximate age of the cluster.
Figure: Figure 21-12 shows an H-R diagram of stars in a cluster. Let's assume that the turn-off point for the main sequence happens at about a surface temperature of 6600 K which corresponds to an F5 spectral class. Using this information can you estimate the age of the cluster? In the figure we clearly see dots corresponding to stars on the main sequence, stars on the red giant branch, and stars on the horizontal branch. (IMPORTANT: in these H-R diagrams we have plotted stars. One does not "connect the dots" in such plots to obtain evolutionary star tracks, although such a bunch of stars may indicate sections of evolutionary tracks. An evolutionary track is the path that describes an individual star's temperature and luminosity as it evolves.) The point where stars leave the main sequence and head up the red giant branch corresponds to the F5 spectral type with a surface temperature of 6600K. The luminosity of such a star is 3.3 Lsun. (I am just giving you this value. Normally you would get it off a table that lists the properties of main sequence stars of different spectral types.) Using the mass luminosity relationship for main sequence stars we find that the mass of this star is 1.4 times that of the sun, and its lifetime on the main sequence is 0.43 times that of the sun, or 4.3 billion years. Thus the cluster is about 4.3 billion years old.
Studies of stellar ages have revealed that there is a difference between the oldest stars and the youngest stars. Young stars tend to have more elements heavier than hydrogen and helium. In the astronomer's terms such stars are "metal rich." (The term Metals refers to anything except hydrogen and helium.) Old stars tend to be metal poor. Young metal rich stars are called Population I and old metal poor stars are called Population II. (A possibly helpful mnemonic: II stars are older than I stars because II is bigger than I.) Globular clusters are old clusters of population II stars. Globular clusters are spherical clusters of stars that are located mostly outside the plane of the galaxy. Galactic, or open clusters like the Hyades or Pleiades, are young, Population I stars.
Here are some learning goals for the study of the Stellar Evolution:
Here are some review questions:
We have talked about star formation and about the main sequence. We have followed stars up the red giant branch after their cores have exhausted the available hydrogen. Now to follow the evolution of stars from this point we need to distinguish between two classes, the low mass stars and high mass stars. We shall see that their evolutions are quite different. Astronomers are not quite certain where the dividing line is between stars that evolve in the "low mass" way and those that evolve as "high mass" stars. But as general classes regard low mass stars as those with masses less than 5-6 Mo and high mass stars as those with masses greater than 10 Mo. The gray area is in between. These two classes end their stellar lives in quite different ways. We begin with the low mass stars.
We have already followed the evolution of the low mass star up to the point where it reached the Horizontal Branch. It is burning helium into Carbon through the triple alpha reaction in its core. As happened at the end of the main sequence lifetime, the nuclear fuel burning in the core eventually is depleted. This time all the Helium has been converted into carbon. What happens next is physically very similar to what happened earlier. The core contracts as the fires die out and helium burning continues in a helium shell surrounding the core. As before, the star again grows in size to become a red giant and the star moves up the asymptotic giant branch in the upper right hand corner of the H-R diagram. These stars are known as AGB stars for short. The core contracts, and electron degeneracy pressure returns as the most important pressure force in the core of the star. The thin layer of helium shell burning is somewhat unstable, that is the burning rate fluctuates a lot. The reason is that helium burning is very temperature sensitive and the star cannot quite get into equilibrium with the helium burning shell. Sometimes the temperature is a bit high and the burning goes rapidly, but then the star expands and the temperature drops. Contraction causes overcompensation and another thermal pulse due to a helium shell flash sets in. These pulses eventually have the effect of blowing off the outer envelope of the star. The expanding shell of gasses thus ejected are called a planetary nebula. (The name has nothing to do physically with planets. It is just that early astronomers who saw these nebulae thought that they looked sort of like distant planets.) When the outer envelope leaves one is left only with the hot core of the star. The core of the star is composed of carbon and oxygen, the oxygen having been formed through the combination of one helium with a carbon. The temperatures in the star are not hot enough to have carbon and oxygen burn so no further nuclear reactions occur. The stars light comes from the trapped residual heat. The core contracts until electron degeneracy pressure provides the support against gravity, after which the star does not shrink as it cools. This star is known as a white dwarf star because of its very high temperature but very small, Earth-sized radius.
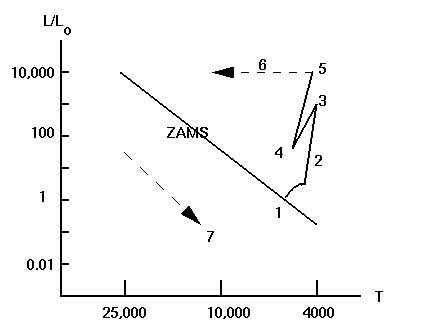 Figure: An H-R diagram showing the
evolutionary track for a one solar massed star. Main features include
(1) Main sequence, (2) Red Giant Branch (RGB), (3) Helium Flash (4)
Horizontal branch, (5) Asymptotic Giant Branch (AGB), (6) Planetary
nebula ejection, (7) White Dwarf.
Figure: An H-R diagram showing the
evolutionary track for a one solar massed star. Main features include
(1) Main sequence, (2) Red Giant Branch (RGB), (3) Helium Flash (4)
Horizontal branch, (5) Asymptotic Giant Branch (AGB), (6) Planetary
nebula ejection, (7) White Dwarf.
There is a relationship between the mass of white dwarf stars and
their radius: the larger the mass the smaller the radius. This is
backward from what you might think, i.e., that as you increase a star's
mass it should get bigger. The reason is that in order for electron
degeneracy pressure to provide support against gravity one needs to
squeeze the electrons together (increase the density). Greater masses
require greater pressure, hence greater squeezing and smaller radii.
Ultimately there is a limiting mass for which electrons can provide
support known as the Chandrasekhar limit. It is equal to 1.4 Mo.
Above this mass electrons cannot provide enough pressure support and
stable white dwarfs do not exist. Thus for stars with masses a few
times that of the sun it is very important for them to blow off most of
their mass in winds and planetary nebulae or they will be too massive
to settle down as a white dwarf star.

This is an image of MyCn18, a young planetary nebula located about 8,000 light-years away, taken with the Wide Field and Planetary Camera 2 (WFPC2) aboard NASA's Hubble Space Telescope (HST). This Hubble image reveals the true shape of MyCn18 to be an hourglass with an intricate pattern of "etchings" in its walls. This picture has been composed from three separate images taken in the light of ionized nitrogen (represented by red), hydrogen (green), and doubly-ionized oxygen (blue). The results are of great interest because they shed new light on the poorly understood ejection of stellar matter which accompanies the slow death of Sun-like stars. In previous ground-based images, MyCn18 appears to be a pair of large outer rings with a smaller central one, but the fine details cannot be seen.
More description of the Hourglass
Nebula. View a full scale image.
 This NASA Hubble Space
Telescope image shows one of the most complex planetary nebulae ever
seen, NGC 6543, nicknamed the "Cat's Eye Nebula." Hubble reveals
surprisingly intricate structures including concentric gas shells, jets
of high-speed gas and unusual shock-induced knots of gas. Estimated to
be 1,000 years old, the nebula is a visual "fossil record" of the
dynamics and late evolution of a dying star. This color picture, taken
with the Wide Field Planetary Camera-2, is a composite of three images
taken at different wavelengths. (red, hydrogen-alpha; blue, neutral
oxygen, 6300 angstroms; green, ionized nitrogen, 6584 angstroms). The
image was taken on September 18, 1994. NGC 6543 is 3,000 light-years
away in the northern constellation Draco.
This NASA Hubble Space
Telescope image shows one of the most complex planetary nebulae ever
seen, NGC 6543, nicknamed the "Cat's Eye Nebula." Hubble reveals
surprisingly intricate structures including concentric gas shells, jets
of high-speed gas and unusual shock-induced knots of gas. Estimated to
be 1,000 years old, the nebula is a visual "fossil record" of the
dynamics and late evolution of a dying star. This color picture, taken
with the Wide Field Planetary Camera-2, is a composite of three images
taken at different wavelengths. (red, hydrogen-alpha; blue, neutral
oxygen, 6300 angstroms; green, ionized nitrogen, 6584 angstroms). The
image was taken on September 18, 1994. NGC 6543 is 3,000 light-years
away in the northern constellation Draco.
More description of the Cat's
Eye Nebula. View a full scale image.
The planetary nebula phase of a star's evolution results in the loss of a great deal of the star's mass. For example, in a one solar mass star the total loss is about 0.35 Mo leaving a white dwarf with 0.65 Mo of mass. This mass loss enables stars that originally had masses as high as 5 or 6 times that of the sun to end up as white dwarves with masses below the Chandrasekhar limit. Note that this also points to a fundamental difficulty facing astronomers working on determining stellar evolution tracks. The evolution of a star depends on its mass. But the star loses mass throughout its lifetime and these mass loss rates are rather uncertain. This leads to some uncertainty as to what the ZAMS mass upper limit for stars that will end their lives as white dwarves. We have observed a white dwarf star in the Pleiades where the turnoff mass is about 7 Mo. There are several white dwarves in the Hyades where the turnoff mass is about 2.5 Mo.
Evolution of a 1 Mo Star:
Time
H-R Location
Energy Source
1010 yrs
Main Sequence
H core burning
108 yrs
Red Giant
H shell burning
108 yrs
Horizontal Branch
He core and H shell burning
107 yrs
AGB
He shell and H shell burning
104 yrs
Planetary Nebula
He shell and H shell burning
forever
White Dwarf
No burning
Now we consider the fate of stars that definitely will not end as white dwarf stars, namely the massive stars with masses greater than 10 Mo. These correspond to spectral classes O, B, and some A stars. The evolution of such stars up through the AGB stage is fairly similar as that of lower mass stars except that everything happens at a much greater pace so the lifetime of each phase is much shorter. This is because the greater masses lead to higher core temperatures and faster nuclear burning. The higher core temperatures also mean that elements heavier than helium can be burned.
We have already noted the similarity between the evolution on the main sequence and the evolution on the horizontal branch. This basic pattern continues in a massive star. The steps are:
We then return to the top of the sequence and repeat with the next fuel. After each cycle we are left with a core that is hotter and denser than before. This means that the heavier elements can burn as fuel. The ever increasing temperature also means that the cycle proceeds faster and faster. As we proceed along the lighter elements are burning in shells surrounding the core. This leads to the term "onion shell" model because each of the burning layers is arranged in a concentric shell like the cross section of an onion. As the various types of nuclear burning begin the luminosity and radius of the star adjusts to the new situation. This causes the evolutionary track to keep moving back and forth across the H-R diagram. But as indicated in the table, this proceeds very rapidly.
Evolution of a 25 Mo Star
Fuel
Temperature
Density (gm/cc)
Time (yrs)
Sample reaction
Hydrogen
4 x 107
5
7 x 106
CNO cycle
Helium
2 x 108
700
5 x 105
Triple Alpha
Carbon
6 x 108
2 x 105
600
12C+12C-->20Ne
+ 4He
Neon
1.2 x 109
4 x 106
1
20Ne+4He-->16O
+ 2 4He
Oxygen
1.5 x 109
107
0.5
16O+16O-->28Si
+ 4He
Silicon
2.7 x 109
3 x 107
1 day
Si --> Fe
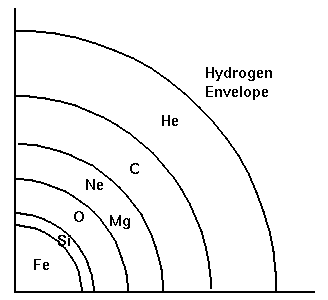 Figure:
Cross-section of a supermassive star after
the iron (Fe) core has formed. The various shells surround the iron
core, each burning a different element.
Figure:
Cross-section of a supermassive star after
the iron (Fe) core has formed. The various shells surround the iron
core, each burning a different element.
Why does the sequence of nuclear burning end with Iron? Iron does not burn because it is the most "tightly bound" of the elements of the periodic table. If an element is to burn by fusion then energy must be given off when that element is combined with another. The new nucleus is more tightly packed together ("bound") than the two separate bits; it would take energy to break the new nucleus apart to the original parts. But with iron we have the situation where to add any other element costs energy, that is the new nucleus is less tightly bound. Indeed, up at the high end of the periodic table we have elements like uranium and plutonium that give up considerable energy when split apart in the process of nuclear fission. Iron then represents the energy minimum and once a star has converted its stuff into iron then it has no further recourse. Something new must happen.
 Figure: An H-R diagram showing the evolutionary
track for a 20 solar massed star. Main features include (1) Main
sequence, (2) Red Giant, (3) Core He burning, (4) Core Carbon Burning,
(5) Triple shell burning (6) Core Neon Burning, (7) Supernova.
Figure: An H-R diagram showing the evolutionary
track for a 20 solar massed star. Main features include (1) Main
sequence, (2) Red Giant, (3) Core He burning, (4) Core Carbon Burning,
(5) Triple shell burning (6) Core Neon Burning, (7) Supernova.
The iron core is initially supported by electron degeneracy pressure and it is surrounded by a silicon burning shell. That shell keeps dumping more and more iron into the core and eventually the core mass approaches the Chandrasekhar limit of 1.4 Mo. Then degeneracy pressure begins to fail and the core begins to collapse. Temperatures and densities soar as the collapse proceeds. The situation is worsened by the following nuclear reaction
e + p -----> n + neutrino
which is the forcing together of electrons and protons to form neutrons and neutrinos. The neutrinos represent an energy loss term since they don't interact much with other matter and can escape from the star. Hence they won't contribute much to the pressure. The high temperatures of the contracting core also produce gamma rays which smash the iron nuclei to bits, undoing in a tenth of a second all the nuclear fusion that went on before. This process, the destruction of nuclei by highly energetic gamma ray photons, is known as photodisintegration. Both of these effects cause the pressure to drop further and the core to collapse further. This is runaway core collapse and in a fraction of a second the core goes from Earth size to about 10 km in diameter. At this point the densities are equal to the density of nuclear material in the form of a ball of neutrons. Neutron degeneracy pressure suddenly takes over and the collapse stops as the core now becomes virtually incompressible. Of course the surrounding star doesn't know that and it continues to hurtle inward. When all this stuff hits the core it bounces and drives a shock wave outward. The escaping neutrinos play an important role in energizing this outward moving shock wave. Normally neutrinos don't interact very well with matter, but here the densities are so great that the neutrinos dump considerable energy into the overlaying layers. In a few hours the shock wave hits the surface of the star and we see the star explode as a Type II supernova. In a matter of days the star brightens by about a factor of 100 million, becoming for a brief time as bright as an entire galaxy. Note: massive stars that explode in this manner are known as Type II supernovae. There is also a Type I supernova that results from an explosion in a binary system. We will discuss Type I supernova later.
Ultimately the source of energy that powers a supernova is gravity. The collapse of a solar mass of material down into a neutron star the size of 10 kilometers releases 1053 ergs of energy which is an enormous amount. This energy emerges in three forms:
Supernovae are rare events. They result only from the most massive stars and only a few massive stars are formed compared to the less massive types. It is estimated that about 3 supernovae occur per century per galaxy. In the modern era all the supernovae that have been observed have been in other galaxies. The last observed supernova in our galaxy was one described by Kepler in 1604. Tycho Brahe saw one in 1572. One of the more famous supernova is the one responsible for the Crab nebula (and the crab pulsar). This was seen by Chinese astronomers in the year 1054. If there are supposed to be three supernova in our galaxy per century, where are all our supernovae? Recall the discussion of dust in the interstellar medium and the fact that there is a lot of obscuring dust in the plane of the milky way. It is likely that this dust blocks our view of most of the supernova in the galaxy and we only get to see the ones that are relatively close by and unobscured.
In any case it had been about 400 years since the last nearby supernova until the year 1987 when a supernova was seen in the nearby (50,000 pc) Large Magellanic Cloud (LMC). This supernova became known as 1987A. The progenitor star was a hot blue B3 supergiant with an estimated mass of about 20 Mo. On February 23, 1987 at 7 hours, 35 minutes, 41 seconds GMT neutrino experiments in Japan and the United States detected a group of neutrinos. As later analysis was to show these neutrinos originated in the core collapse leading to supernova 1987A. This detection confirms important aspects of our theory of massive stars: the total energy released in neutrinos and the long (10 second) escape time required for the thermal neutrinos. Two hours later at 9:22 GMT recorded visual observations of the LMC reveal nothing unusual. But a plate taken at 10:38 (and examined the next day) showed a 6th magnitude star where none was before. At 5:30 GMT February 24 astronomer Ian Shelton noticed a 5th magnitude star on a photograph he had taken of the LMC. The discovery was immediately announced and astronomers all over the southern hemisphere began an intensive study of 1987A.
Figure 22-8 shows light curve for SN1987A, a Type II supernova. A light curve shows the history of the apparent magnitude versus time. The explosion of a massive star creates a Type II supernova. Typical light curves show rapid rise to maximum brightness, and then a long period of exponential decline.
A study of the light curve for the supernova reveals the basic behavior of the visual appearance. The first stage is a very rapid rise in the apparent magnitude, by about 7 magnitudes (103 in brightness) with in a few hours. This corresponds to the arrival of the shock wave at the stellar surface. Over the next few days a slower rise occurs as the supernova grows brighter. This gradual brightening is due to the increase in size in the expanding supernova envelope which allows us to see deeper into the hotter regions. Eventually the supernova reaches its peak brightness. For 1987A this was about a factor of 10 below the normal peak brightness of supernovae. It is believed that the relative faintness of 1987A was due to its progenitor star being a smaller blue supergiant instead of a red supergiant. After the peak, the supernova slowly grows fainter as the shell cools. This leads to an exponential decay phase. The supernova shell continues to be energized by the decay of short-lived radioactive nuclei, in particular cobalt 56. The detection of such short-lived nuclei confirms our theory that the elements of the periodic table are produced in massive stars and that enriched material is thusly returned to the interstellar medium in the supernova explosion.
 Figure:
A supernova remnant. This is the Crab
Nebula, the leftover ejecta from a supernova explosion that took place
in 1054 and was recorded in the records of Chinese astronomers. The
remnant is kept glowing by energy from the rotating neutron star
("pulsar") at its center.
Figure:
A supernova remnant. This is the Crab
Nebula, the leftover ejecta from a supernova explosion that took place
in 1054 and was recorded in the records of Chinese astronomers. The
remnant is kept glowing by energy from the rotating neutron star
("pulsar") at its center.
After the supernova has exploded we are left with whatever remains of the star's core and an expanding shell of gas known as a supernova remnant. The core may consist of a neutron star or a black hole (to be discussed later), or, in some cases it may get blown apart completely leaving nothing behind. Astronomers hope that in a few years (when "the smoke clears") a neutron star will be seen in the place where 1987A occurred. Let's focus on the supernova remnant (SNR) expanding into space. After things have quieted down this remnant continues to expand and can grow in size to between 10 and 100 parsecs. It is after all moving at speeds of around 100 km/sec, which gives a size of 20 pc after only 100,000 years. The remnant continues to glow because it is continually shocked by impact with the interstellar medium. The gas in the shell produces many emission lines and emission in X-rays and radio. As the expanding shell moves through the interstellar medium it sweeps up material to form a giant bubble. The appearance of an SNR is basically spherical but there are random filamentary structures throughout. Recall that these shock waves and swept up bubbles are possible mechanisms for initiating star formation. In any case the SNR is returning material enriched by heavy elements back into the interstellar medium.
This brings us to the important issue of nucleosynthesis, or the creation of the nuclei. The universe is mostly composed of hydrogen and helium. All the rest of the elements of the periodic table are built up in the interior of stars through nuclear reactions. Now the Earth is mostly composed of elements other than hydrogen and helium. More personally, the atoms in our bodies are carbon, oxygen, hydrogen and nitrogen, plus lots of additional important trace elements. This means that the gas that formed the solar system must have been enriched through stellar evolution and supernovae.
We have previously seen how the more massive a star the further it can get up the periodic table in its nuclear reactions. In the massive stars that go supernova elements up to iron are produced by fusion processes. But what about all those elements above iron? We have said that fusion doesn't work for those because it takes energy to create them. However, if there are a lot of neutrons around then one can add neutrons without too much of an energy penalty because neutrons, being neutral, do not feel any repulsive electrical force from the protons in the nuclei. Late in a massive star's life and certainly during a supernova, neutrons are produced in great abundance. There are two processes which are identified as important mechanisms for the production of elements beyond iron: the s-process and the r-process, s for slow, r for rapid. The general mechanism is that nuclei are hit by a neutron. The new nucleus is unstable to a radioactive process known as beta decay where a neutron decays into a proton and emits an electron and a neutrino. (Recall again the direct observation of short-lived radioactive elements such as Cobalt 56 in supernova 1987A. These observations provide direct evidence for these neutron absorption processes in supernovae.) In turning a neutron into a proton we move up one atomic number in the periodic chart. In the slow process this radioactive decay occurs before the nucleus is hit by another neutron. In the rapid process there are so many neutrons that the nuclei are hit by several before radioactive decay occurs. (Note: the old alchemist's dream of turning lead into gold doesn't work. Lead has an atomic number (number of protons) of 82 while gold has an atomic number of 79. The s- and r-processes imply that supernovae do it the other way around. They turn gold into lead!) The challenge for the astrophysicist is to understand the cosmic abundances of all the elements in terms of these fusion and neutron processes.
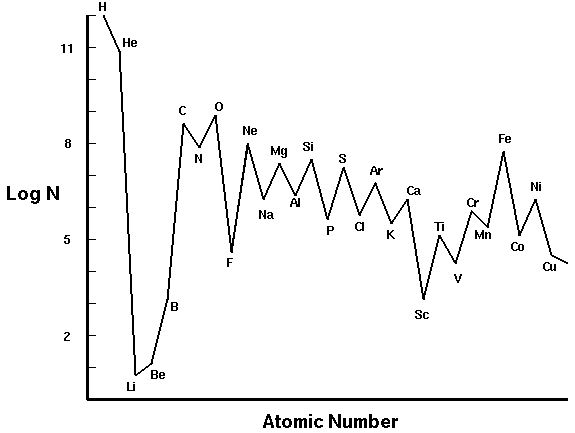 Figure:
Relative cosmic abundances for the
different elements. There are peaks at carbon, oxygen, neon and iron
corresponding to important elements in nucleosynthesis. The peak at the
end of the chart is lead, the element with the largest atomic number
that is still stable.
Figure:
Relative cosmic abundances for the
different elements. There are peaks at carbon, oxygen, neon and iron
corresponding to important elements in nucleosynthesis. The peak at the
end of the chart is lead, the element with the largest atomic number
that is still stable.
Here are some learning goals:
Here are some review questions:
We have already discussed how the end state of the cores left behind in many supernovae are neutron stars. In doing so we use a relatively recent result in supernova theory. Although neutron stars were predicted in 1934 by Zwicky and Baade, it was not until 1968 that a neutron star was detected in the core of the Crab supernova remnant. Zwicky and Baade's original proposal that there should be neutron stars followed a careful (and in retrospect more than reasonable) line of argument. The only stellar remnant known at the time was the white dwarf supported by electron degeneracy pressure. Why couldn't there be an even more compact star, packed down to nuclear densities, composed entirely of neutrons and supported by neutron degeneracy pressure? Such a beast would be the most dense thing in the universe.
The suggestion of Zwicky and Baade was ignored by the astronomical community. The idea of a neutron star just seemed too far out. But with hindsight we can see why a neutron star is both necessary and an expected outcome for at least some paths of stellar evolution. Suppose all supernova end up leaving behind a white dwarf remnant. Chandrasekhar had shown that there was an upper limit to the mass of a white dwarf (the Chandrasekhar Mass). Above that mass electron degeneracy pressure could no longer resist the force of gravity. But what of a supernova that didn't have the foresight to relieve its core of all but 1.4 Mo of mass? Astronomers just assumed that although they didn't know the details of the mechanism, somehow the star must accomplish that feat so that supernovae produced white dwarves. Note that even if white dwarf stars were the only core left by supernova, the white dwarves might gain additional mass later through accretion. What would happen then?
As we know now, there is a kind of compact stellar remnant which is more massive than the white dwarf, namely the neutron star which was predicted by Zwicky and Baade. A neutron star is a star compressed to nuclear density, composed mainly of neutrons, and supported by neutron degeneracy pressure. Neutron stars are likely to come in masses between 1.4 to about 3 Mo. The upper limit would correspond to the point where neutron degeneracy pressure is no longer enough to provide support, although the exact value of this limiting mass is not known. The size of the neutron star is about 30 kilometers in diameter. If you have a solar mass compacted into such a small size you know that its going to be dense and indeed it is, on order of 1014 gm/cc. If the Earth were compacted to this density it would be a couple hundred meters in diameter. Of course with an object like a neutron star with a large mass but a small radius, one has an enormous surface gravity, 1012 times that of the Earth. The escape velocity from the neutron star is about half the speed of light.
The discovery of neutron stars in 1968 was a product of then relatively new science of radio astronomy. At that time astronomers were filtering out the short term variations in the radio signal (static) in favor of measuring the average intensities of celestial radio sources. One of the pioneering radio telescope establishments was at Cambridge University in England. As astronomer there, Antony Hewish, decided to study the rapid variations that would result because of the radio wave's passage through the stream of ionized gas given off by the sun known as the "solar wind" (in particular the electrons in the solar wind can affect radio waves). However, Cambridge graduate student Jocelyn Bell found something more remarkable: regular radio pulses coming from a certain location in the sky. The pulses had a frequency of 1.3373011 seconds. As time went by more and more of these pulsars were detected, but the question remained: what are they?
To understand the issues involved we must first point out that the rate at which something pulses sets an upper limit on its size. Specifically something cannot produce sharp, regular, rapid pulses if the pulse period is shorter than the light travel time across the object. For example, suppose the sun blinked on and off at its surface. The sun's surface is not at equal distances from us. The center of the face of the sun is closer to us than the limb or edge of the disk. This creates a light travel delay. If the sun blinked off instantaneously we would see a wave of darkness beginning at the center and moving out to the edge over a period of about two seconds due to this light delay effect. Hence if something varies sharply in a second it size must be less than a second times the speed of light. Pulsars must be associated with small objects, such as white dwarves and neutron stars.
Next, what mechanism produces the pulses? The variations in brightness that is producing the pulse might originate in an oscillation or a rotation. Calculations show that oscillating white dwarves have too long a period whereas oscillating neutron stars have too short a period. How about rotation? If there were a hot spot on a rapidly rotating object then one would see pulses of emission. An analogy is provided by the beam of a searchlight, or a lighthouse: its bright only when the beam is pointing at you. But what kind of star can rotate once every second? If it were a white dwarf star (which is about the size of the Earth) rotating once every second the centrifugal force would be so great that the white dwarf would be torn apart. A neutron star on the other hand, which is the size of a city, can rotate at that speed without breaking up. Therefore the most likely model involves a rotating neutron star.
 The case was "clinched" by the discovery of a pulsar in the center of
the crab nebula
supernova remnant. This was the remains of the
supernova that exploded in 1054 AD and which was recorded by chinese
astronomers. Since compact neutron stars are the likely outcome of
Type
II supernova explosions, the discovery of a pulsar in the heart of
the Crab makes the association between neutron stars and pulsars all
the more certain. The crab is pulsing at a rate of about 30 pulses a
second. When it was discovered, this was the fastest rate of pulsing
for any pulsar. Since we are able to assign a date to the supernova
that gave birth to this pulsar we also know that the crab is a very
young pulsar. In addition to the radio pulses the Crab also pulses in
optical light. Most pulsars do not have such optical pulsations.
Those that do are generally associated with relatively recent
supernova. We associated fast pulse rates and high energy with
recently formed pulsars.
The case was "clinched" by the discovery of a pulsar in the center of
the crab nebula
supernova remnant. This was the remains of the
supernova that exploded in 1054 AD and which was recorded by chinese
astronomers. Since compact neutron stars are the likely outcome of
Type
II supernova explosions, the discovery of a pulsar in the heart of
the Crab makes the association between neutron stars and pulsars all
the more certain. The crab is pulsing at a rate of about 30 pulses a
second. When it was discovered, this was the fastest rate of pulsing
for any pulsar. Since we are able to assign a date to the supernova
that gave birth to this pulsar we also know that the crab is a very
young pulsar. In addition to the radio pulses the Crab also pulses in
optical light. Most pulsars do not have such optical pulsations.
Those that do are generally associated with relatively recent
supernova. We associated fast pulse rates and high energy with
recently formed pulsars.
Speaking of recent supernova, does 1987A have a neutron star pulsar in it? At the present moment we can't say because our view in toward the center is blocked by all the high energy material in the expanding supernova remnant. However when this stuff clears out, perhaps in a few years, we should get a direct glimpse of our youngest pulsar to date. It should prove very interesting.
Why are neutron stars rotating so rapidly? It has to do with angular momentum which is the scientifically defined quantity associated with spin or rotation. Angular momentum is a quantity that is "conserved," that is to say neither increases nor decreases in value within a closed system. Conservation is a property also associated with linear momentum (straight line motion) and energy. Now in a spinning object the amount of angular momentum is given by the angular speed of the matter located at some distance r around the central point. For a given lump of mass m located at r from the center and rotating with an angular velocity of omega, the angular momentum is given by L = mr2omega. The important thing about this formula is the realization that conservation of angular momentum means that decreasing the radius increases the rate of spin omega. The common example is the ice skater who pulls in their arms in order to spin faster. Another example is a diver who, after leaving the diving board, goes into a tuck in order to spin rapidly, then goes out of the tuck to reduce the spin rate. Now back to stars: A star is spinning during its lifetime. For example the sun rotates once every 25 days at its equator. If you shrank the sun from its present radius of 7 x 105 km down to neutron star size of 20 km, a factor of 35,000, then the angular velocity would increase by a factor of one billion to a rotation period of 2 milliseconds. So clearly there is enough angular momentum available to make neutron stars spin at very rapid rates.
Now how are the radio pulses produced? The answer to this lies with the neutron star's magnetic field. Most stars are believed to have some amount of magnetic field associated with them. When the star collapses this magnetic field is locked into the star and is compressed and magnified in strength. Hence neutron stars are should have a very strong magnetic field. If the magnetic field isn't exactly aligned with the spin axis then the north and south poles will spin around with the star, each one visible alternatively. Now a rapidly spinning strong magnetic field can produce radiation as particles are accelerated along the magnetic field lines. Thus the magnetic fields produce beams of radiation along the magnetic pole directions. As the poles sweep by our line of sight we see the beam momentarily leading to a pulse of radiation. The first pulse corresponds to one of the magnetic poles and the next pulse corresponds to the other magnetic pole. Generally one pole produces a brighter pulse than the other because we will tend to be looking more along the line of sight to one of them.
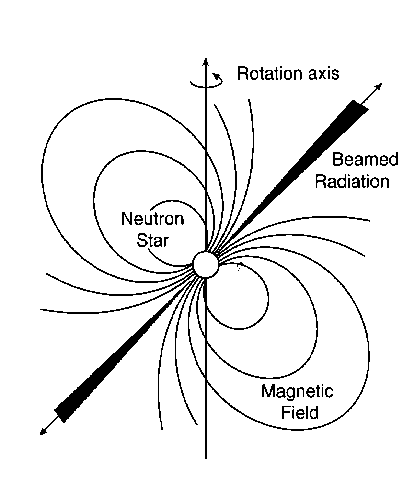 Figure: The magnetic field of a neutron star
produces beams of
radiation which emerge along the magnetic axis. This Lighthouse
effect causes periodic flashes. The pole more aligned with our line
of
sight produces stronger pulses.
Figure: The magnetic field of a neutron star
produces beams of
radiation which emerge along the magnetic axis. This Lighthouse
effect causes periodic flashes. The pole more aligned with our line
of
sight produces stronger pulses.
The rate of pulsing in a pulsar gives one the rotation rate in the neutron star. The rotation rate is very slowly changing as the pulsar spins down. This occurs because their magnetic fields interact with surrounding matter to transfer spin angular momentum and rotational energy from the neutron star to that matter. Pulsars slow down very gradually, but because there is so much energy inherent in a spinning neutron star, even a modest decline in spin rate means an enormous amount of energy transferred out from the pulsar. The rate at which the crab nebula is energized is equal to the energy lost by the spinning neutron star. This gives us another means of identifying the age of a neutron star. Generally rapidly rotating pulsars are young. The Crab pulsar and the Vela pulsar have periods less than 0.1 second. There are hundreds of other older pulsars with periods between 0.1 and 4 seconds.
How does the spin energy of the crab pulsar get turned into visible light? The Crab nebula is glowing with synchrotron radiation a form of radiation given off when high speed electrons are accelerated by magnetic fields. Recall that light is electromagnetic radiation. When electrons, which are charged particles, are accelerated by magnetic fields, they produce time-changing electromagnetic fields, i.e., radiation. Synchrotron radiation is the name for the type of radiation emitted by electrons moving close to the speed of light in the presence of magnetic fields. Two things are required: high speed electrons and magnetic fields. The magnetic field is anchored in the pulsar and the electrons are ripped off of the surface of the neutron star and accelerated outward at very high speeds and energies.
Occasionally a slight speedup is observed in a pulsar's rotation rate. Such a pulsar glitch is believed to be caused by a slight decrease in the neutron star's radius brought on by a "starquake." Basically the gradually slow down of the pulsar reduces the centrifugal forces acting on it and the star contracts at its equator. But this contraction is not continuous; rather, it is sudden. As the solid/crystalline crust contracts suddenly we get a starquake-induced glitch in the rotation rate.
The pulsars with the shortest known periods are known as the millisecond pulsars. These pulsars have periods as short as between one and two milliseconds and their periods are very constant. The fact that they don't slow down much implies a weak magnetic field, but doesn't their fast rotation speed imply that they are very young (and hence should have a strong magnetic field)? The clue to the answer lies in the fact that most millisecond pulsars are found in binary systems. It is believed that millisecond pulsars are old pulsars that have had their spin rates increased through the accretion of angular momentum containing matter from the other star in the binary. Mass transfer has spun up these pulsars back to very fast spin rates. The idea that the millisecond pulsars are actually old systems gains support from the presence of millisecond pulsars in globular clusters.
Now let us return to considering what happens in close binary systems when the binary contains a compact star such as a neutron star or a white dwarf, plus a regular star that is filling its Roche lobe. Sometimes in these semidetached binary systems the mass transferred from one star to another doesn't actually fall directly down onto the compact star but instead goes into orbit around that star. This material forms a disk orbiting around the compact star known as an accretion disk. Gas in an accretion disk can become very hot and glow in visible, UV and X-ray light. Accretion disks can lead to many interesting types of phenomena, particularly when they are located around neutron stars and black holes.
A neutron star in a binary system is capable of additional tricks. When X-ray satellites were first launched on rockets and balloons in the 1960's many X-ray sources were discovered. (Recall that X-rays cannot penetrate the Earth's atmosphere to reach the ground and so must be observed from space.) Orbiting satellites provide a more complete picture of the X-ray sky. Many of the X-ray sources are believed to be binary systems where one of the two stars is a neutron star. Matter transfer occurs from an ordinary star toward the neutron star. This gas goes into orbit forming an accretion disk. The gas slowly spirals in until it is caught by the neutron star's magnetic field. Then the gas is directed by the magnetic field onto the pole of the neutron star where it finally hits the surface. When the gas collides with the surface it is heated to a very high temperature and generates X-rays producing a pulsing X-ray source.
The transfer of matter onto a compact star such as a neutron star or a white dwarf can also produce explosive processes. One of these is the nova, characterized by an abrupt increase in brightness but only by a factor of a million (as opposed to 100 million in a supernova). A nova is caused by hydrogen accreted onto the surface of the white dwarf. As more and more hydrogen builds up on the surface the temperature rises. The material is degenerate so when the temperature becomes high enough for nuclear burning to take place it does so explosively producing a nova. An X-ray burster is a similar object except that it involves degenerate helium burning on the surface of a neutron star. As hydrogen accretes onto a neutron star (possibly producing a variable X-ray source) the hydrogen is promptly burned into helium. The helium accumulates until the temperature is high enough for a degenerate helium burning explosion.
A binary system is responsible for another type of supernova, namely the Type I supernova. We have already discussed Type II SN which result from the core collapse at the final stage in the evolution of a massive star. The two classes are distinguished observationally by the presence (Type II) or absence (Type I) of hydrogen lines in the light of the supernova. Type I supernova are due to a carbon-oxygen white dwarf in a semi-detached binary system. The other star is transferring mass over onto the white dwarf. Recall that the white dwarf is supported by degeneracy pressure which is limited to supporting a total mass less than the Chandrasekhar mass (1.4 Mo). When more mass is piled onto the white dwarf its mass gets perilously close to this limit. The temperature in the interior of the dwarf goes up and eventually gets to the point where carbon burning can begin. Just as in the case of the earlier-discussed helium flash the thermonuclear burning runs away: the rapid increase in temperature doesn't increase the amount of degeneracy pressure so the star can't cool and remain in equilibrium. What happens is an explosion due to run away nuclear reactions. The white dwarf rips itself apart in a type I supernova. (Note: given the naming conventions we have the following statement: Population I stars produce Type II supernova. Population II stars produce type I supernova.)
One of the most unusual binary systems known is a system called SS433. SS433 caught the public's fancy some time back because it was known as the "star that is both coming and going." It got this name because emission lines were seen that were both redshifted and blueshifted. There were also lines that were basically stationary. The redshift and blueshift were in phase and both had a 164 day period. The interpretation of this system was that there were two beams of gas jetting out from the compact object's accretion disk (or the compact object itself). One jet was approaching us (the blueshifted lines) and one jet was receding (the redshifted lines). The jets were precessing over a 164 day period, hence the time variability seen in the redshifts and blueshifts. Radio observations have since confirmed this basic picture as we see radio emission coming from two oppositely directed colinear areas. A corkscrew pattern in the radio emission confirms the picture that the jets are precessing.
At the present time no-one has a complete theory of how these jets are produced. Indeed there is some controversy as to whether the compact object producing the jets is a neutron star or the more exotic object known as a black hole. The importance of SS433 stems from the fact that we see great jets emerging from such energetic systems as quasars and galaxies (to be discussed later). Presumably if we could understand the behavior of this relatively nearby binary system we could then understand what is going on in distant galaxies.
Another remarkable binary system is the binary pulsar. This was discovered in 1974 by Joe Taylor of Princeton University and Russell Hulse (U Mass). They found a pulsar had a period that wasn't very regular; this is not what one would expect for a pulsar. They eventually realized that the effect was due to the 8 hour orbit of the pulsar around another body. It turned out that the other star is also a neutron star although not one from which we can detect pulses. Since 1974 two more binary pulsar systems have been found. The 1974 binary pulsar has been studied for almost twenty years now. One of its most remarkable results has been a confirmation of a particular aspect of Einstein's theory of general relativity. Specifically this is the prediction of the generation of gravitational radiation by accelerated masses. Gravitational radiation amounts to "ripples" in the geometry of space-time (a phrase which in the present context will be nearly meaningless but sounds good). The binary pulsar's orbit has been affected by the generation of these waves. Suffice it to say that gravitational waves carry off a little bit of the orbital energy and allow the orbits to slowly spiral together (VERY slowly). Because of the fine quality of a pulsar as a timing device it is possible to directly measure this inspiral and compare it to theoretical predictions from Einstein's theory. They match to high accuracy, providing a stunning confirmation of the theory of general relativity. (Hulse and Taylor won the 1993 Nobel Prize for physics for the discovery of this binary pulsar.)

Figure: Data from the binary pulsar. The change in the period
of the orbit (Delta P) versus time. If Einstein's theory is correct,
the period changes orbit because of loss of energy due to the emission
of "gravitational radiation." It is a small effect; only a few
seconds over several years. The dots are the experimental
data, the curve is the prediction from Einstein's theory of general
relativity. The agreement is remarkable.
Now we have alluded to how a neutron star is the next stage once a
stellar remnant becomes too massive to be supported by electron
degeneracy pressure as a white dwarf. Since neutron stars are
supported by neutron degeneracy pressure there must also be an upper
limit to the mass of a neutron star. Although this mass is somewhat
uncertain it probably lies between 2 and 3 Mo. What happens
when the mass is too large? What is the next stage in compactness?
What holds up the star against gravity when neutron degeneracy fails?
The answer is...Nothing! Gravity wins and collapse continues forever.
The star becomes a black
hole.
Here are some learning goals for the study of the Stellar Evolution:
Here are some review questions:
The neutron star is similar to the white dwarf: it is a massive, compact star that is supported entirely by the pressure coming from tightly packed elementary particles. In the case of the white dwarf these were electrons surrounding the atoms. For a neutron star the atoms themselves have been crushed down into one giant nucleus, composed of neutrons. White dwarf stars have an upper limit for their masses, called the Chandresekhar mass. Any more mass and the electrons can no longer provide enough support. By analogy there must be stars whose masses are sufficiently great that they cannot be supported by neutron degeneracy pressure as a neutron star. This is called the Oppenheimer-Volkov limit. The exact value of the Oppenheimer-Volkov limit is not known but probably is around 2-3 solar masses. What sort of star would we have if we exceeded this limit?
The first clue comes from considering the escape velocity of a star. The escape velocity is the speed you need to go to escape from the gravitational pull of an object. The formula for the escape speed from an object of mass M with radius R is
v = (2GM/R)1/2
You can increase the escape speed from an object either by increasing its mass or decreasing its radius. For compact stars like white dwarfs and neutron stars an increase in the mass results in a decrease in radius. This means increasing the mass of such a star will lead to a big increase in escape speed. Neutron stars are so massive (big M) and so small (small R) that the escape speed from the surface of a neutron star is about half the speed of light. What would happen if the escape speed got to the point where it was faster than the speed of light? Clearly light would not be able to escape and you wouldn't see the object. The black hole is such an object.
The first ideas of objects corresponding to black holes were posited in just such a manner, that there might be extremely dense compact objects whose escape speed exceeded the speed of light. The actual theory of black holes depends, however, on the theory of general relativity. General relativity (GR) is Einstein's crowning theoretical achievement. GR replaces the theories of Newton for describing how things move and respond to gravitational forces (Newtonian mechanics). We will say more about GR in a moment. Suffice to say a present that a theory of black holes depends upon GR. Newtonian theories will not give you the correct properties of black holes. The apparent weirdness of black holes is due in part to the fact that you are more intuitively familiar with the ideas in Newtonian theory than with relativity.
The size of a black hole can be found by setting the escape velocity equal to the speed of light c and solving for radius. (Actually, the escape velocity formula above is Newtonian and hence isn't necessarily applicable to black holes. But it turns out to give the same answer as the GR solution so we use it for demonstration purposes.) Doing this yields
Rs = 2GM / c2
We refer to this size as the Schwarzschild radius after Karl Schwarzschild who first derived it in the context of general relativity theory. Now this is a very small radius. For one solar mass the Schwarzschild radius is 3 kilometers; for the Earth it corresponds to one centimeter. This means that if you compacted all the mass of the sun into a ball of size 3 kilometers then gravity becomes overwhelming and nothing can escape.
Now you may have a picture in your mind of a dense, compact object sitting there "sucking" light onto its surface. The actual situation is far stranger because the star that forms a black hole is not going to be static: it must collapse down to zero radius, R=0, and infinite density. Here's why: All along our basic picture has been the battle between the attractive force of gravity and the supporting force of pressure. A pressure force, however, must be communicated upwards through the star, say by the impact of molecules, or by electrostatic forces, or the motion of degenerate particles. In the black hole state gravity is so strong that its pull exceeds the ability of even light to escape, or, for that matter, even to move upward. Hence no pressure force can be communicated from lower to upper layers in the star. No message can be sent from "down below" to hold the star up. Collapse is inevitable. In fact, any pressure that is present contributes to the collapse! This is because pressure is a form of energy and energy is equivalent to mass (by Einstein's formula) hence energy contributes to the total gravity.
You may wonder at this point how gravity communicates upward if pressure can't. One way to think about it is to remember that gravity forces exist out away from an object. Changes in the gravitational force travel at the speed of light. If the sun were to be removed from our universe by some strange superbeings we would still feel the sun's gravity until the information about the disappearance of the sun propagated to us at the speed of light. So when a black hole forms it leaves behind its gravitational field which continues to affect things.
A black hole consists therefore of an infinitely dense singularity at R=0 surrounded by the Schwarzschild radius from which no light can escape. This radius is known as the Event Horizon. It is the horizon beyond which you cannot see any events (an event being an occurrence at some point in time and space). It is the location from which nothing can emerge, not even light. You can think of it as the point in space where the gravitational attraction is so great that you would have to move outward at the speed of light just to stand still. (Think of trying to swim upstream against a strong current as an analogy.) The horizon is a location, not a solid surface. Things can pass inward but nothing can pass out. Thus a black hole can increase its mass by acquiring material falling in through the event horizon, but it cannot decrease in mass or break into two parts or anything that would result in information or matter escaping from within the horizon.
These comments allude to the strange properties of black holes. Black holes are hard to understand because they involve Einstein's Theory of Gravitation, known as General Relativity. Obviously we can do little more than sample some of the weird ideas that result from Einstein's theory, but that should be enough to make you wonder about some of your intuitions regarding space and time.
Begin by thinking about Newtonian physics. Newtonian physics roughly corresponds to our intuitions about how the universe operates, although the even older "Aristotelean" physics is even more intuitive in some respects. Anyway, Newton begins with the idea that space and time are separate absolute entities: absolute space stretches off in three dimensions in all directions, forever, and absolute time advances forward at a steady, unchanging rate forever. Objects remain in a state of uniform motion (constant velocity) unless acted upon by a force which produces an acceleration proportional to the mass according to the formula F=ma. Gravity is one such force and gravity acts between masses across space according to the formula F=GmM/R2. Mass enters the equations in two ways: once as an inertia, i.e., a resistance to the application of a force (larger mass, less acceleration for the same force), and as the generator of gravitational force, i.e., more mass means more gravitational force. Mass is conserved, meaning the total mass in a closed system remains constant forever. Energy, something that manifests itself in many forms, e.g., energy of motion, heat, gravitational, is also and separately conserved.
Einstein's theory of General Relativity begins from another starting point: Einstein assumes that the Laws of physics and the speed of light are absolute, that is they are independent of position or motion through space. This is not true under Newton's assumptions which gave space and time separately the absolute status. If time and space have absolute status then the laws of physics and the speed of light vary depending on one's motion. Einstein's assumptions requires that space and time must be different for different observers, that is time and space measurements are relative. This is a terribly nonintuitive concept. For example Einstein's relativity implies that if I observe somebody going by in a spaceship at high speed I will observe their shipboard clocks running slowly compared to my clock. A trip to Alpha Centari at .99 the speed of light would take about 4 years as I measure time but only a week as measured on board the spaceship. Relative motion alters the measurements of space and time.
Now Einstein's next fundamental assumption is that uniform acceleration is entirely equivalent to gravitational pull. That is the physics one observes while sitting in a laboratory on Earth in the one gee gravity field would be identical to that observed in a spaceship far from the Earth that is accelerating at one gee of acceleration. This is known as the Principle of Equivalence. Since Acceleration equals Gravity, and Motion (and hence acceleration) affects space and time, then gravity itself distorts space and time. In fact the gravitational force results from distorted (or "curved") spacetime.
A common misconception is that the gravitational field of a black hole is somehow qualitatively different from the gravity of more ordinary objects. This is not true. It is only more intense, and to feel that intensity you have to be close to the black hole. Einstein's theory of gravity is true for any gravitating body, but the effects become extreme in the vicinity of a black hole. What are some of these effects? The first effect we will consider is that of time: a clock near a black hole will run slow as measured by an observer away from the black hole. Time runs slower down in a gravitational field. Again this is true even for weak gravitational fields such as here on the Earth: a clock at sea level runs slower than a clock at higher altitudes. Along with this effect comes a gravitational doppler shift. Light coming out of a gravitational field is redshifted; light falling into a gravitational field is blueshifted. Imagine launching a space probe down towards a black hole. The probe sends back signals every second as the probe measures time. It beams back its message using a red laser light beam. As it falls we will measure the interval between signals to be longer than a second, with the interval constantly increasing. The red laser light will be shifted down to infrared and then radio frequencies. As the probe approaches the event horizon its time seems to stop and the light is infinitely redshifted and eventually no more signals emerge. We never see the probe reach the event horizon as it takes an infinite time as we measure time.

Figure: Two observers, one near a black
hole, one far away, compare the effect that gravity has upon light
beams and clocks.
The situation from the probe's point of view is quite different. It continues to transmit its signals at regular intervals. But it sees time speeded up in the universe around it. Light beams falling in toward the black hole are increasingly blueshifted. It approaches the black hole with increasing speed (approaching the speed of light) and falls in in a very brief period of time as it measures time.
If you were to fall into a black hole the thing that would kill you would be the tidal force. The tidal force (so named because it accounts for the tides on the Earth) is due to a body receiving different amounts of gravitational force. If you were falling feet first into a black hole, your feet, being closer to the black hole, would receive a greater amount of gravitational force than your head. Your feet would wish to fall faster than your head, the net effect of which would be that your feet would be pulled downward and your body stretched out. Your skeleton, muscles, etc. would resist that as long as possible, but eventually the tidal force would stretch you out too far! The amount of tidal force depends on the size of the black hole and the size of the body falling in. If the horizon isn't too much bigger than your body size you will be torn apart before you pass through the horizon and into the black hole. With really big black holes you can get through the horizon before being torn apart. This is a small comfort.
Once inside the horizon of a black hole, there remains nothing that prevents further infall. Everything that falls into the hole continues to fall until it reaches the center, at R=0. Here all the mass in the hole is crushed into zero volume and infinite density. This strange place is called the singularity, and it is a point where the laws of physics, as we understand them, must break down. A description of the singularity would require a theory that combines gravity (general relativity) with the physics of the very small (quantum mechanics). This theory is called quantum gravity, and it has not yet been formulated. We don't know what happens within the extreme region of the singularity.
Black holes might seem to be very complicated beasts, since they have so many strange properties. But actually they are remarkably simple. The only part of a black hole that affects the universe at large is that part that is outside the event horizon, namely the gravitational field. The gravitational field of black holes is fully described by just three basic parameters: the mass of the hole, its rate of spin, and any electrical charge that the black hole has. If matter falls in then the mass of the hole will increase by the amount of mass that fell in and the gravitational field will adjust. Electric charge will also be remembered: a black hole with charge would attract charges of the opposite sign. However, it is expected that all black holes will be electrically neutral for just this reason: if they were to become charged they would attract oppositely charged particles until they became neutral again.
More important is the spin of a black hole. If a black hole is formed out of rotating matter then it will remember that rotation. The gravitational field outside of the black hole will reflect that rotation. A spinning black hole is sometimes called a Kerr hole, after Roy Kerr who first formulated the equation describing its properties. An interesting property of a Kerr hole is that space-time itself is dragged around the hole in the direction of the hole's spin. For example if you were falling into a black hole on a path you thought was straight in, the distant observer would see you begin to spiral around the black hole. You, the infalling observer would see the stars above you begin to rotate around. An analogy might be to think of space itself being sucked into a vortex like water around a bathtub drain. The particle floating on the water will be dragged into a spiraling course by the flow of water. The infalling observer is dragged into a spiral by the flow of space-time.
Nothing that goes down a black hole ever comes out. Right? Not exactly. Recall that Einstein's equations of general relativity imply that gravity is equivalent to matter and energy. This means that the gravity of a black hole can in principle be tapped for energy. Steven Hawking discovered that a black hole actually emits radiation, although this radiation is very small. How does it do it? It relies on the strange world of quantum mechanics. The so-called Heisenburg uncertainty principle tells us that energy needn't be conserved for short intervals of time, as long as it is conserved over a longer time interval. The more energy you `borrow' the quicker it has to be paid back. So what happens is that empty space is alive with particles and antiparticles that appear and disappear, all within the little interval of time allowed by quantum mechanics. These are called virtual particles. Can a virtual particle become real? Yes if it can get the energy from somewhere to "pay off its loan before it comes due." Near a black hole these virtual particles are created and destroyed in the vacuum of space. But, near the horizon the tidal stress is strong (for some holes) and that stress from the tidal force can be used to give virtual particles enough energy to live. So a virtual particle and a virtual antiparticle are created near the horizon. The tidal force gives them enough energy to survive as real particles. One particle goes down the hole and the other escapes. This process will be more efficient the greater the tidal stress. As we discussed before, tidal stress will be greatest in small holes, so small holes will emit more particles. But for the Hawking radiation to be very significant the hole has to be very small, a minihole.
Hawking radiation is very strange, but undoubtably is a real (albeit minuscule) effect in black holes. There are other weird things that probably are not found in nature. One of these is the wormhole. It turns out that the mathematics of the Schwarzschild solution admits the possibility of a wormhole, that is the throat of the space-time funnel connects to another space-time funnel that is somewhere else. Could a wormhole then be a bridge or gateway to distant places or other universes? Alas, not the Schwarzschild wormhole. All paths through the wormhole that avoid the singularity at R=0 are paths that require you to go faster than the speed of light. Recent research by Kip Thorne and colleagues at Caltech examined the wormhole question in more detail. The found a situation where perhaps a wormhole could be constructed with a route that a timelike path could follow. It requires exotic conditions to bring about and its still not certain whether or not it violates physical laws or conditions. So could there be wormholes? Maybe, but don't bet on it unless you get long odds.
Now black holes are a phenomenon predicted by the equations of Einstein's theory of general relativity. However, we have never directly seen or measured a black hole. How indeed would we "see" a black hole? We can't see anything from with the hole but we can detect how the black hole affects things outside the horizon. For example we can see gas that is falling into the hole if it emits light before it passes through the event horizon. This is likely to happen if, for example, the black hole is located in a semi-detached binary system and mass is flowing from one star through the Lagrange point toward the black hole.

Figure: Cygnus X-1. One of the best
candidates for a black hole system is an X-ray source in the
constellation Cygnus. A 30 Mo B0 supergiant is overflowing
its Roche lobe and dumping mass into a massive compact star. X-rays are
emitted by the hot gas.
A good candidate for just such a binary system is Cygnus X-1, an X-ray source in the constellation Cygnus that was detected by a satellite in 1970. Apparently the system consists of a B0 supergiant that is dumping mass into a compact companion. The companion has a mass that is greater than 6 Mo which is larger than the upper limit for a neutron star. The X rays are coming from an accretion disk which is formed when the gas goes into orbit around that compact object. If the gas falls down toward the black hole it gains speed (and hence energy) from falling in a gravitational field. If the gas collides with other particles of gas the velocities are turned into heat. Hence spiraling into a strong gravitational field causes the gas to become very hot. The gas can get sufficiently hot that it generates X-rays. The X-rays are observed to vary rapidly. Recall that rapid variations indicate that the emission is coming from a small region, with size less than the distance light can travel in the time interval of the variation. This indicates that the X-rays are emerging from a very small region of space. Thus we have an object, very small, too massive to be a neutron star, and with strong enough gravity to heat gas to X-ray temperatures. The only thing consistent with those data is a black hole. Astronomers are a skeptical lot however, so they continue to try to think of alternatives to the black hole model. So far no good alternatives have been proposed.
There are a few other binary systems that have unseen companions with large mass. There are additional systems that have X-ray variations that are quite similar to those seen in Cygnus X-1. Thus evidence is gradually accumulating in support of black holes in binary systems. Another possible location for black holes is in the center of galaxies. It may be that at the center of many galaxies there lurk huge supermassive black holes. We will discuss this possibility later in the section on Quasars and Active Galaxies.
Another way that we might be able to detect black holes would be through gravitational radiation. Gravity waves are ripples in the shape of space itself produced by rapidly changing gravitational fields. One event that might produce a large gravitational wave would be the collision of two black holes. If there were black holes in a binary system they would slowly spiral together. When they merge they would produce considerable gravitational radiation as the new more massive black hole settles down to a stationary spherical shape. At the present time work is proceeding on the establishment of a gravity wave detector system. This system, called LIGO (Laser Interferometer Gravitational wave Observatory), consists of two 5 km long evacuated pipes that lie perpendicular to each other. Laser beams are shot down the pipes. If a gravitational wave passes through the lengths of the pipes will change in certain ways and this would modify the light travel time of the laser beams. The length changes are about 1 part in 1020 so the is an incredibly difficult experiment. But the hope is that it would be able to detect black hole collisions and neutron star collisions anywhere in a region of about 100 Million parsecs around us.

Figure: LIGO, the gravitational wave
observatory. The lengths of two pipes, set perpendicular to each other,
are measured with laser beams. A gravity wave will cause the length of
the pipes to vary by a tiny amount.
One final effect that is worth mentioning is the gravitational lens effect. Light traveling through a strong gravitational field will be bent; basically the light will fall downward just like anything else. Thus a black hole passing within our line of sight to a star or galaxy will distort our image of that star or galaxy, just like a lens. In fact gravitational lenses have been observed although in all cases the object doing the lensing is a galaxy, not a black hole.

Figure: A gravitation lens is produced when
light passes through the gravitational field of a cluster of galaxies.
The arcs seen in this picture are the distorted images of more distant
galaxies.
Here are some learning goals for the study of the Milky Way.
Here are some review questions:
We take up next the large systems composed of many stars that are known as galaxies. In particular we will focus upon the Galaxy that our sun is located within, namely the Milky Way Galaxy.
In the sky the Milky Way is a faint, diffuse band of light that stretches across the heavens, clear across the celestial dome. To the naked eye it is just a dim light, but when viewed with a small telescope it resolves into individual stars in vast numbers. Seeing these stars we can recognize that our sun is part of a huge system that is in the shape of a disk; the Milky Way is the disk seen edge on.
But where is the sun located within this disk of stars? If one simply examines the Milky Way it appears as if it is more or less equally bright in all directions. This suggests that we are in the center of the disk. If we were at an edge then it would be noticeably brighter on one side and quite dim in the opposite direction. This is what lead astronomers (in the last century and the early part of this century) to conclude that we were in fact near the center of a disk-like system of stars. This point of view was, however, incorrect. Our sun is not located at the center of our Galaxy but out about two thirds to the edge. What was not realized was that there is so much interstellar dust creating interstellar extinction that we can't see very far, and certainly can't see to the actual center. This makes the Milky Way appear more uniform than it would otherwise be.
In 1915 the astronomer Harlow Shapley was studying globular
cluster systems. In particular he was using variable stars to
measure distances to globular clusters. Variable stars are stars whose
luminosity varies with time as the star pulsates. In particular there
is a class of variable star known as Cepheid
Variables. The stars vary by about one magnitude over periods
ranging from one to 100 days. These variables are located in a certain
region of the HR
diagram known as the "instability strip." This strip lies up above
the main sequence near the red
giant region. Stars pass through the instability strip as they
evolve back and forth in and out of red giant phases during the late
stages of their evolution. While they are in the instability region of
the HR diagram the star tends to expand and contract as the surface
layers heat and cool. What happens is the surface layers start out
rather opaque and thus block the escape of radiation. This causes the
surface layers to expand outwards. There comes a point where the
opacity of the layers drops off and suddenly the light and heat can
escape more freely. The outer layers cool off and begin to contract.
The whole process is rather like an engine, cycling back and forth:
heating, expanding, cooling, contracting. The important observational
property of these stars is the relation between their average
luminosity and the period of their oscillation: the larger the
luminosity the longer the period. One needs to develop a specific period-luminosity
relation for each class of variable star. The Cepheids are higher
luminosity variables and they come in two varieties: Type I is the "metal
rich" type, meaning they have lots of elements other than hydrogen and
helium (to an astronomer everything except hydrogen and helium is
called a "metal"), and the Type II or metal poor Cepheids. Type IIs are
dimmer than Type Is. Low mass, post helium flash stars form the
variable class known as RR
Lyrae variables. These are located at the low luminosity end of the
instability strip and they have periods less than a day.
Now given the period-luminosity relationship we can measure the
period of variable stars and from that derive their luminosity. This
allows us to measure the distance to that variable star by comparing
the apparent with absolute magnitude (the distance
modulus). Notice that this assumes that there has been no interstellar
extinction due to dust.
If dust is present you would have to correct the apparent magnitude for
this effect.
Harlow Shapley mostly used RR Lyrae variables, but in any case he made use of the period-luminosity relationship and he found that the globular cluster systems were far away and centered, not around the sun, but around a point nearly 10 kiloparsecs away in the direction of the constellation Sagittarius. From this he made the remarkable conclusion: the globular clusters were centered on the actually center of our Galaxy and we were out on the edge of the disk. This turned out to be the correct interpretation of the data.
We now have a more complete picture of the Milky Way. It is composed of several elements. One, the most obvious, is the disk of the Milky Way. The disk is where we live, some 8 kpc out from the center. The disk is not very thick, only about 0.6 kpc wide. However, its total radius is probably from 12-15 kpc. The disk is composed mainly of Population I type stars. There is considerable gas and dust, so much so that we can only see out through the disk for a distance of about 3 kpc. There are spiral arms within the galactic disk. The spiral arms contain considerable gas and dust and are often associated with active star formation and HII regions. Recall in the discussion of star formation and the interstellar medium we indicated how the compression wave associated with a spiral arm in a galaxy might initiate star formation. The disk is rotating around the center of the Galaxy. The rotation accounts for its flattened shape and for the spiral in the spiral arms. The spiral arms trail out in the direction opposite the rotation.
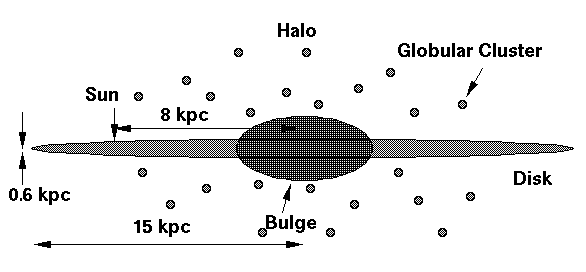
Figure: The shape and structures of the Milky
Way Galaxy. The disk extends for about 15 kiloparsecs in radius, and
the Sun is about 8 kpc from the center. The globular clusters orbit in
the halo around the center. Harlow Shapley used the distribution of
globular clusters to determine the location of the center of the
Galaxy.
Near the center there is another structure known as the galactic bulge. This is a more or less spherical distribution of stars centered on the galactic nucleus, i.e., the very heart of the Galaxy. The bulge is composed mainly of metal rich older stars. Surrounding the whole system, and outside the plane of the disk is the galactic halo. This is where the globular clusters live. As we have discussed previously, the globular clusters are composed of old Population II (metal poor) stars. Because they live outside the disk they can be seen even though they are far away because one doesn't have to look through so much interstellar dust in order to see above the plane of the Galaxy. Notice that both the bulge and the halo contain older stars. It is likely therefore that they were amongst the first structures formed when the Galaxy was created.
Now let's consider the disk of the Galaxy. One of the key tasks in figuring out the structure of the Milky Way is to compute the motion of the sun through space. The relative velocities of other stars can be obtained with doppler shifts and proper motions. But we will need to know how the sun moves in order to understand stellar motions with respect to the center of the Galaxy. It is difficult to measure the sun's motion just from the stars near us because they share the same rotational motion about the Galaxy and they more or less move with us. An alternative method of determining the sun's motion is to obtain doppler shifts of globular clusters and nearby galaxies located outside the disk of the Milky Way and then determine the average doppler shifts of those objects. The assumption is that the galaxies and globular clusters have more or less random motions. It is certainly the case that they are not rotating around the center of our Galaxy. By comparing the averages we can see if there is any systematic difference and from that determine the sun's motion. The result shows that the sun is moving at a speed of around 250 km per sec in the direction of Cygnus.
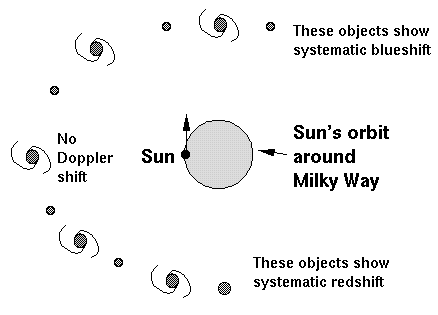
Figure: Looking for systematic red and
blueshifts in nearby external galaxies and globular clusters tells us
the Sun's orbital velocity around the center of the Galaxy.
As we discussed before when considering the mass of the sun, the orbital speed of an object is determined by the mass around which that object is orbiting. Here we can use the Sun's orbital speed to estimate the mass of the Galaxy. In the case of the orbits of the planets around the Sun we use something called Kepler's Law. This law was written in terms of masses and gravitational force by Isaac Newton. Here we will use Newton's law for orbital motion in the following form:
M(R) = R V2 / G
where M(R) is the mass of the Galaxy within radius R and V is the velocity at that radius. If you plug in the numbers for the sun and work this through you get about 1011 Mo for the mass of the Galaxy inside the location of the sun's orbit (at about 8 kpc). This roughly the number of stars within that radius.
By getting the doppler shifts to other stars and to gas clouds we
can plot out the rate of rotation at all distances within the Galaxy.
With Newton's form of Kepler's law we then have a way of measuring mass
versus radius throughout the whole Galaxy. A plot of orbital speed
versus the distance from the galactic center is known as a rotation
curve.
The rotation curve along the above formula points to mystery
regarding the Galaxy. Notice that if the velocity is held constant in
that formula, the Mass must increase as the radius increases (G is a
constant). Hence, the fact that orbital speeds do not drop off outside
the orbit of the sun indicates that there continues to be significant
amounts of mass present, right out to the edge of the luminous galactic
disk. If there were no more mass as the radius were increased then V
would have to drop of as the square root of radius (to hold M constant
in the formula.) What the rotation curve means is that there is a lot
of mass out beyond the visible limits of the galaxies. This implies the
existence of some form of dark, non-luminous matter in the halo of the
Galaxy. What kind of stuff could it be? Some of the possibilities that
have been considered are small nonluminous stars, bodies similar to
Jupiter, black
holes. There is currently a search underway for such objects which
go by the name of MAssive Compact Halo Objects (MACHO).
The search is being carried out by looking for gravitational lens
effects due to these compact objects passing in front of stars in the
Large Magellanic Cloud, a neighboring small galaxy.
 Figure: The Large Magellanic
Cloud
Figure: The Large Magellanic
Cloud
An entirely different sort of candidate is provided by some previously unknown massive elementary particle. Such things go by the name of Weakly Interacting Massive Particle (WIMP). The important aspect of these particles is that they have mass but they don't really interact with ordinary matter very much. One candidate for a massive elementary particle is the neutrino. In our discussion of Supernova 1987A we mentioned how neutrinos do not interact very well with ordinary matter. Currently the neutrino is believed to have zero mass (like the photon, no mass just energy). However, it is difficult to prove experimentally that the neutrino has zero mass. If it has a small but finite mass then it could gather in great abundance and produce a substantial gravitational field. These neutrinos would otherwise be undetectable. If in fact neutrinos have no mass there might be other particles, as yet undetected, that could fulfill the same role. Thus particle physicists have some interest in what the astronomers learn about this dark "missing mass."
Obviously it is rather difficult to learn things about the disk of
our Galaxy since we live inside it. But through careful observations we
can learn things about the disk's structure. The extinction due to dust
means that we can see only about 3 kpc away from the sun but that is
enough to tell that there are four spiral arms in our vicinity. This is
determined by locating young OB associations and related star forming
regions. Young star clusters are associated with the spiral arms in a
galaxy.
A more powerful technique is to look in the radio wavelengths for
the presence of atomic hydrogen, HI. Atomic hydrogen gives off
radiation at a wavelength of 21 centimeters. This type of emission was
discussed in the section on the interstellar
medium (see also lecture notes on The
Interstellar Medium). As a reminder it is the radio emission that
comes from the difference in energy between a proton and its electron
(the hydrogen atom) with their "spins" aligned and one where their
spins are anti-aligned. If the electron flips from being aligned to
being antialigned it goes from a higher to a lower energy state and
emits a photon. The wavelength of that photon is 21 cm. So 21
centimeter radiation can be detected wherever there is atomic
hydrogen present, and atomic hydrogen is present in great abundance in
the spiral arms of the Galaxy. Now if we look in a given direction
through the Galaxy with out radio telescope our line of sight will cut
across several spiral arms. The arms will each be moving with a
different velocity hence each arm will have its own characteristic
doppler shift. From a complete survey of the plane of the Milky Way we
can reconstruct a complete picture of the distribution of HI, and from
this deduce that the Milky Way has significant spiral structure, much
like other galaxies.
How do spirals arms form in a galaxy? The fact that the galaxy isn't rotating as a rigid body means that it is natural to expect spiral structure. Differential rotation is very good at producing spirals although the amount of winding tends to be very high so the spiral would be tightly wound after a few orbits. Since many of the spirals in external galaxies are a lot less tightly wound there must be more going on that simple winding by differential rotation. Two of the prevailing ideas are as follows: First, we have the "chain reaction theory" in which star formation triggers nearby star formation and so on. Differential rotation then takes these local areas of star formation and drags them out into a spiral pattern. As star formation dies out in one area it starts up in others so small spiral patterns are constantly forming and fading out. This results in a chaotic, ragged and weak spiral structure. This matches some galaxies (called the "flocculent" spirals), but not the so-called "grand design" spirals where there are two or three large clearly defined spirals present.
Figure: A Hubble Space Telescope image of
the heart of the spiral galaxy M100 in the Virgo Cluster of galaxies.
Note the large spiral arm features outlined by dust lanes bordered by
regions of hot stars and gas indicating active star formation.
An alternative spiral-making mechanism is known as the spiral density wave mechanism. To understand this we need to appreciate that the spiral pattern is not made up of fixed groups of stars, but exists as an independent spiral wave moving through the stars. In this sense it is like a water wave which moves through water but doesn't move the water itself. The ripple just travels along, the water goes up and down in response, but the water stays basically where it is. In spiral galaxies the wave is made of correlated elliptical orbits of stars. This creates a slight bunching in the number of stars at certain positions around the disk. The pattern itself moves at a much slower speed than the stars themselves, 30 km/sec versus 200 km/sec. As stars pass through the wave they bunch up a bit, but not much happens to them. However when gas clouds pass through the wave they can collide and be compressed triggering star formation. Thus we find lots of star formation and its effects associated with the spiral wave pattern. In particular spiral waves feature lots of bright young stars, OB associations, and HII regions. Now, what causes those correlated elliptical orbits to form? We need some sort of nonspherical gravitational field. Such gravitational fields can be produced by a neighboring galaxy exerting a tidal gravitational field, or by the presence of a "bar" in the center of the galaxy. A bar is a nonspherical galactic bulge. Spiral galaxies with companions and spiral galaxies with bars at their center ("barred spirals") often have very strong spiral structure. We shall take up the classification of galaxies in our next chapter.
Finally let's focus on the center of our Galaxy and the mystery there. As mentioned repeatedly, the galactic nucleus is not visible in optical light. It can be studied, however, in light from other parts of the electromagnetic spectrum. Recall that dust affects blue light more than red light. Infrared and radio wavelengths are not affect much by the presence of the dust. Hence, from the ground we can observe the galactic center in radio. Indeed, the galactic center is a very powerful radio source known as Sagittarius A (Sag A for short): the "A" designates the most powerful radio source located in that part of the sky called Sagittarius. (Other powerful radio sources, like Centarus A or Cygnus A, are other galaxies.) There is radio emission over a large region extending along the plane of the Galaxy. Sgr A is located at the galactic center. Within Sgr A there is a smaller concentration of radio emission which seem to be the actual center. This point is called Sgr A* and it appears to emit mainly synchrotron radiation. Detailed radio observations of the region around Sgr A* made with the Very Large Array (VLA) radio telescope, located in New Mexico, reveal a complex structure of loops and rings in high energy, synchrotron radiation-emitting gas. These structures are about 1 pc in size and extend over a region of about 60 pc. The presence of synchrotron radiation and the shape of the arcs and loops strongly suggests powerful magnetic fields are present.
We can also observe the galactic center in X-ray and gamma ray wavelengths. Basically those photons are too powerful to be stopped by the dust. Such observations must be done by orbiting satellites, so it has only been in relatively recent years that we have been able to study the galactic center in these wavelengths. X-ray observations have revealed a number of X ray sources. Many of these are likely to be binary X-ray systems. One of them seems to correspond to the location of a source that is emitting powerful gamma rays from the annihilation of electrons with positrons (matter-antimatter annihilation). It was once thought that this powerful gamma ray source corresponded to the actual galactic center but it is now apparent that it is offset from Sgr A*.
The presence of matter-antimatter annihilation, plus all the X-rays
and radio emission suggest that unusual things are happening in the
center of our Galaxy. One hypothesis is that the center of our Galaxy
contains a black hole. This wouldn't be your garden variety black hole
but a supermassive
black hole with a mass perhaps a million times that of the sun. One
of the arguments in favor of such a mass is the large velocities
observed in the stars and gas at the center. Large velocities imply
large orbital speeds and large orbital speeds imply a large mass around
which the orbit is located. Some calculations suggest that about a
million solar masses are required with in a very small region, say 0.04
pc. There is some controversy about this however. And the discovery
that the gamma ray source is not at the center has made the case for
the black hole less compelling. It may be that everything can be
accounted for just with neutron stars and dense, active star clusters.
Here are some learning goals for the study of galaxies:
Here are some review questions:
Today we take the enormity of the universe and the existence of other distant galaxies as a given. It is just part of the accepted picture. At the beginning of the twentieth century, however, this was not the case. The idea of external galaxies was only a hypothesis, and a not widely held one at that.
Galaxies were unknown to the ancient astronomers. There are only a few significant galaxies visible to the naked eye (e.g., the LMC, the SMC and the great galaxy in Andromeda) and these appear to be fuzzy patches of light. What the first telescopes provided was not much of an improvement; they were still fuzzy patches of light. In the late 18th century, astronomer Charles Messier compiled a catalogue of fuzzy patches of light to aid his search for comets (which also appear to be fuzzy patches of light). Many of the objects in the Messier catalogue of nonstellar objects are, in fact, galaxies. More and more of these fuzzy "nebulae" were discovered as astronomers studied the skies with their ever improving telescopes. In the nineteenth century the third Earl of Rosse, using a large telescope that he had built, discovered a spiral pattern in M51, one of Messier's fuzzy objects. Such objects with spiral patterns became known as "spiral nebulae."
At the beginning of this century the big question was whether or not the nebulae were entities that lived with in our Milky Way, or were instead far away and "Milky Ways" (i.e. galaxies) in their own right. The discussion culminated in the so-called "Shapley--Curtis Debate" in 1920. Two astronomers, Harlow Shapley and Heber Curtis got together and debated the question "are the nebulae associated with our galaxy?" Shapley, who as you will recall first measured the size of the Milky Way by studying variable stars in globular clusters, argued that our galaxy was so huge that these other nebula had to be relatively nearby and therefore much smaller. Curtis had seen novae in the nebula and had used the assumption that those novae would have the same absolute magnitude at maximum light. This allowed him to estimate the distance to the nebulae and the distances were sufficiently large that they had to be independent objects. Shapley's arguments were flawed by the fact that his computation of the Milky Way's size was too large by a factor of three (he had been thrown off, in part, by interstellar extinction which made the Cepheid's appear to be dimmer, and hence at a greater distance than they really were.)
The question was finally settled in 1924 by Edwin Hubble.  Hubble,
using the 100 inch telescope at Mount Wilson, resolved the Andromeda
galaxy into individual stars and found Cepheid
variables. Using the Cepheids
as his distance indicators Hubble determined the distance to the
Andromeda "nebula." The distance was large enough to demonstrate
unambiguously that it was an independent object and not part of our
galaxy. The distance to the Andromeda galaxy is about 680 kpc,
a distance which is about 30 times the diameter of our galaxy. The
Andromeda Galaxy (also known as M31) is a spiral galaxy very similar to
our own Milky Way. It is slightly bigger. It has a disk filled with
young population
I stars and appears
very blue, and a bulge filled with older reddish stars. It is
difficult to see the spirals clearly because we see the galaxy close to
edge on.
Hubble,
using the 100 inch telescope at Mount Wilson, resolved the Andromeda
galaxy into individual stars and found Cepheid
variables. Using the Cepheids
as his distance indicators Hubble determined the distance to the
Andromeda "nebula." The distance was large enough to demonstrate
unambiguously that it was an independent object and not part of our
galaxy. The distance to the Andromeda galaxy is about 680 kpc,
a distance which is about 30 times the diameter of our galaxy. The
Andromeda Galaxy (also known as M31) is a spiral galaxy very similar to
our own Milky Way. It is slightly bigger. It has a disk filled with
young population
I stars and appears
very blue, and a bulge filled with older reddish stars. It is
difficult to see the spirals clearly because we see the galaxy close to
edge on.
 Figure: The great galaxy in Andromeda. This is an
example of a
Spiral Galaxy, probably similar to our own Milky Way. The discovery
by Hubble of Cepheid variables in Andromeda allowed the distance to
this galaxy to be determined, thus demonstrating the existence
of independent galaxies outside the Milky Way.
Figure: The great galaxy in Andromeda. This is an
example of a
Spiral Galaxy, probably similar to our own Milky Way. The discovery
by Hubble of Cepheid variables in Andromeda allowed the distance to
this galaxy to be determined, thus demonstrating the existence
of independent galaxies outside the Milky Way.
Having demonstrated the existence of external galaxies, Hubble set about the task of classifying galaxies according to their shape and appearance. The results of his work are now known as the Hubble Classification Scheme, and it continues to be widely used in astronomy today. Hubble defined three main classes, elliptical galaxies, spiral galaxies, and irregular galaxies.
The ellipticals are so-named because of their elliptical shape. The ellipticals are subclassified by their degree of ellipticity as they appear to the observer. E0 types are completely spherical, and E7 types are very elliptical (i.e., elongated). E1 through E7 have increasing degrees of ellipticity. They are smooth and structureless, and contain mainly old Pop. II type stars. There is little evidence for an extensive interstellar medium, or active star formation. For example, 21 cm emission from neutral hydrogen is generally absent from ellipticals. Ellipticals have no disk component. They show no systematic rotation, although the stars in them are moving about. Their orbits, however, are oriented in all directions. Ellipticals range in size from the relatively rare Giant Ellipticals, which can be as big as a Megaparsec across with a trillion stars, to the very common dwarf ellipticals which can be as small as a kiloparsec across with a million stars. Some giant ellipticals are exceptions. They seem to have disks of gas and dust and evidence for star formation. Some astronomers think that such galaxies may be the result of a recent collision. In this case the giant elliptical has swallowed a companion spiral!
 |
Figure: The galaxy NGC7479 is an example of a Barred Spiral. |  |
Figure: The giant elliptical galaxy M87 at the heart of the Virgo cluster of galaxies. |
Spiral galaxies, or type S, have a disk component and a bulge. All spirals have these two components; otherwise spirals have considerable variation. S0 type galaxies appear sort of intermediate between ellipticals and other spirals. They have a disk component but little evidence for spiral arms, and appear to be short of dust and gas. Other spirals are classified by the tightness of their spiral winding and the size of their bulge, and whether or not the bulge contains a bar, which is an elongated structure sticking through the central bulge. Spirals with prominent bulges and tightly wound spirals are called Sa spirals. Sb and Sc spirals have increasing less prominent bulges and less tightly wrapped spirals. If the spiral has a bar then the designation is SBa, SBb and SBc. The Milky way is is an Sb type (or possibly an SBb, it would be difficult to detect a bar even if it is there) with an intermediate sized bulge and moderately wrapped spirals. All spirals share characteristics with the Milky Way in that the spiral arms contain considerable numbers of new stars and HII regions and the disk in general contains young population I stars and lots of interstellar medium. Spirals themselves are not necessarily young, but they do have enough gas to have active ongoing star formation. The spiral arms contain emission from many young O and B stars, while the bulge regions are reddish due to lots of K and M type stars. The Milky Way is a typical spiral.
 Figure: The Small Magellanic Cloud is an
irregular galaxy that
is a member of the local group of galaxies. Another irregular local
group member is the Large Magellanic Cloud. These galaxies are
visible only in the southern hemisphere.
Figure: The Small Magellanic Cloud is an
irregular galaxy that
is a member of the local group of galaxies. Another irregular local
group member is the Large Magellanic Cloud. These galaxies are
visible only in the southern hemisphere.
The last Hubble classification, the Irregular galaxies, have no obvious shape. Irregular galaxies tend to be smaller than spirals but bigger than dwarf ellipticals, with between 100 million and 10 billion stars in them. They are grouped into subclasses Irr I for irregulars containing pop. I stars and Irr II for those containing old pop. II stars. The Irr I galaxies look a little like spirals, but the relatively rare Irr II galaxies show very strange shapes. Irregulars come in a variety of sizes. Dwarf irregulars, like dwarf ellipticals are probably very common although they are hard to detect at great distances since they don't have lots and lots of stars. Many times irregular galaxies are associated with a larger galaxy. The Large and Small Magellanic clouds are examples of dwarf irregular galaxies that orbit around the Milky Way.
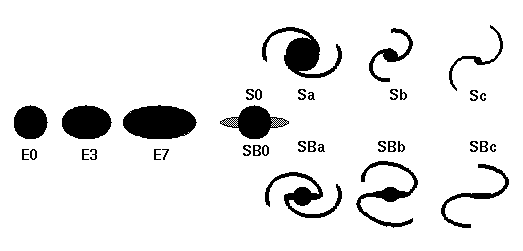
Figure: The Hubble galaxy classifications, arranged in the traditional "tuning fork" pattern.
What do the different Hubble types mean? They are not an
evolutionary sequence, that is, we don't think that spirals evolve into
ellipticals or vice versa. The various types of galaxies appear to be
fundamentally different. Ellipticals have low amounts of organized
angular momentum, consist mostly of old stars, and have little dust and
gas. The disks of spiral galaxies have high amounts of angular
momentum, have lots of dust and gas, and lots of young stars. These
galaxies must have formed in different ways but we are not sure why or
how. There are intriguing clues like the fact that there are more
spirals out away from clusters, and fewer spirals within dense
clusters. Maybe the environment where the galaxy formed plays a role
in the type of galaxy that gets formed.
Let us next take up the subject of finding distances to galaxies. If we are to take the measure of the universe we will have to be able to find these distances, but, as you can well imagine, the task becomes increasingly daunting the further you go out. The whole thing is based on something known as the distance ladder. This is the series of steps by which we set the various standards to be used in determining distances to other increasingly distant objects.
The Distance Ladder
| Object | Distance (pc) | Method |
|---|---|---|
| Sun, Solar System | 10-6 | Radar, Orbits |
| Alpha Centari | 1 | parallax |
| Hyades Cluster | 40 | Hipparcos parallax |
| Galaxy | 104 | Cepheids, Main Sequence Fitting |
| Andromeda | 105 | Cepheids, SN, OB stars |
| Virgo Cluster | 107 | HST Cepheids, OB stars, SN |
| Beyond | 108 and up | Brightest Galaxies, Tully-Fisher |
The first step, which we discussed at the beginning of the course, was simply to determine the distance from the Earth to the Sun (one AU). Parallax methods can then be applied (using the Earth's orbit as a baseline) to obtain the distances to the nearest stars. An important step in the distance ladder is the determination of the distance to the Hyades cluster. The moving cluster method is used to determine the distance to the Hyades which comes out to be about 45pc. The reason that the Hyades is important is that it contains lots of representative stars which can be used to calibrate the HR diagram main sequence. Then we can look at more distant clusters and use the process of main-sequence fitting, or spectroscopic parallax to obtain a distance. As we have seen Cepheid variables and RR Lyrae stars provide another means of obtaining distances, so long as we have calibrated the Period-Luminosity curves with variable stars whose distances have been obtained through other means. Cepheid variables can be seen in galaxies out to about the Virgo Cluster (100 Mpc distance), but they are too faint to be seen in more distant galaxies. Bright O stars can be used, or the luminosities of supernovae which come to specific maximum luminosities at their brightest. The idea in all of this is to come up with things called Standard Candles, that is objects whose luminosity (and hence absolute magnitude) is known. The further out we go, the brighter the standard candle must be. For the most distant galaxies we can no longer detect individual stars so we must be content with the luminosities of the brightest galaxies as standard candles. Unfortunately, as standard candles go, bright galaxies aren't really very good because there is quite a bit of intrinsic variation in a galaxies brightness.
One of the more recent developments in distance indications is the Tully-Fisher relation which holds that there is a correlation between the velocity of the gas in a spiral galaxy (as measured by the variation in the doppler shift in, for example, the 21 centimeter line), and the absolute magnitude of the galaxy. As we have seen, velocities relate directly to the mass of the galaxy through orbital mechanics (Kepler's laws). It appears that the total luminosity is also directly related to the mass (this is often called the mass to light ration M/L of a galaxy). The idea is therefore that the variance in the doppler shift of the 21 cm line in a spiral galaxy gives you a direct measure of its intrinsic luminosity. If you can get enough galaxies together with distances determined by some other method, you can get a calibrated relationship between the 21 cm observation and the absolute magnitude.
It is easy to see why measuring distances is a process fraught with peril. Each new distance indicator, each new standard candle, requires calibration from objects whose distances depend upon other techniques. Each stage depends on the correct measurement of closer distances, all the way back to the measurements of the distances within the solar system. An error at any early stage will propagate throughout the entire distance ladder. And don't forget the effects of interstellar extinction (dust) on the measurement of apparent magnitudes. How much light is lost between here and some distant galaxy due to dust? Its a hard question to answer.
Now let's return to the discussion of the astronomer Hubble. Hubble, you will recall, determined the distance to the Andromeda galaxy by finding a Cepheid variable star there. This settled the question as to whether or not the spiral nebula were galaxies. Hubble was able to observe Cepheids in other galaxies as well and so obtain distances to them. At about the same time it had been noticed that most of the galaxies ( nee nebulae) that had been observed had rather large redshifts. They all seemed to be moving away from us with large velocities. What Hubble did was to plot the redshifts of the galaxies versus the distances to the galaxies. From this he found that there was a direct linear relation between distance and redshift: the further a galaxy was from us, the faster its recession velocity. This relation, which has come to be known as Hubble's Law, is written
v = Ho R
where v is the recession velocity, R is the distance to the galaxy, and Ho is the constant of proportionality known as Hubble's constant.
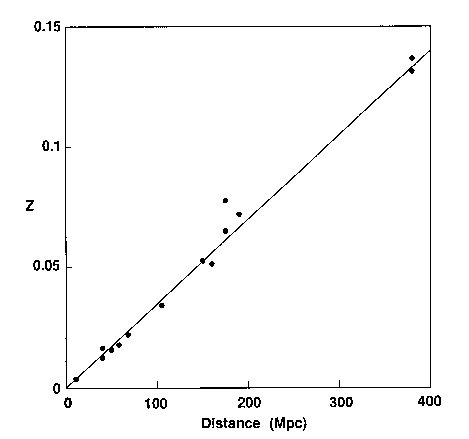
Figure: A redshift versus magnitude plot reveals a linear
relationship between recession velocity and distance.
The determination of the Hubble constant requires measuring redshifts and obtaining distances to galaxies by independent means, as described above. Once distances are obtained they can be plotted against the observed recession velocity. One then fits a straight line to the data points and obtains the slope of the line. This procedure yields a value of the Hubble constant. Several groups have done this and have obtained various values for Ho. One group has obtained a value of 50 km/sec/Mpc. What that value means is that the recession velocity increases by 50 km/sec for ever Megaparsec in distance. For example, a galaxy at a distance of 3.5 Mpc would have a recession velocity of 175 km/sec.
It should be noted that other groups have obtained different values of the Hubble constant, values such as 100 km/sec/Mpc and 75 km/sec/Mpc. The differences are related to issues dealing with distances to remote galaxies, such as the type of standard candle one is using, or the amount of interstellar extinction one factors in to correct the apparent magnitudes. It is good enough for our purposes to be aware that some uncertainty exists (a factor of 2) in the value of Ho and to proceed by selecting one or another of the values to use.
For relatively nearby objects, Hubble's law itself becomes a way to determine distances. (The reason why we are restricting ourselves to "relatively nearby" galaxies we will discuss in a moment.) Suppose you had a galaxy in which you found an emission line of sodium, which has a rest wavelength of 590 nm, shifted to 620 nm. What is the distance to that galaxy using Hubble's Law? First, compute the redshift:
z = (lambda - lambdao) / lambdao = (620 - 590)/590 = 0.05
Now recall that for speeds much less than the speed of light, z=v/c, hence this galaxy is receding at a speed that is 5 percent the speed of light, or 0.05 x 3 x 105 = 1.5 x 104 km/sec. Using a value of the Hubble constant of 50 km/sec/Mpc we can now solve for the distance in Megaparsecs:
1.5 x 104/50 = 300 Mpc.
Notice that if we use another value for the Hubble constant we would get another distance. For example, some astronomers believe that the Hubble constant is closer in value ot 100 km/sec/Mpc which would give us a distance to that galaxy of 150 Mpc. The best way to talk about galaxies, in absence of a definite value of the Hubble constant, and in absence of a good model for the large scale properties of the universe, is to simply give the observed value, namely the redshift, when describing galaxies. The redshift becomes a quantity that substitutes for distance when speaking of the most remote galaxies.
What is it that is making the galaxies rush away from us? It is important to realize that this doesn't mean that we are in the center of some big explosion, or that the galaxies are rushing out to fill up an otherwise empty space. Although we shall discuss it at greater length in the section on cosmology, it is worthwhile mentioning here that the Hubble flow is due to an overall expansion of space itself. The distances between all galaxies are being scaled up, everywhere. This means that if you were in another galaxy looking about, you would see galaxies expanding away from you according to the Hubble flow. Every galaxy seems to be in the center of this uniform expansion. This expansion is part of the basic structure of the universe.
What are the potential pitfalls in determining distances via Hubble's Law? First we need to distinguish the types of velocities that are measured when we measure redshift. The first type is due to the expansion of space and this is the velocity accounted for by Hubble's law. However, you will recall that galaxies also move on orbits. Galaxies in a cluster of galaxies will move around on orbits within that cluster. The Andromeda galaxy is moving toward the Milky Way. These velocities will be present in addition to any Hubble expansion velocity. This additional random velocity (as opposed to the systematic Hubble velocity) goes by the name peculiar velocity. When we take redshifts of galaxies we will have to take into account the fact that they can have peculiar velocities toward or away from us with magnitudes anywhere up to 1000 km/sec. A way around this difficulty is to obtain the average redshift of a cluster of galaxies and assume that that is representative of the Hubble redshift. The problem also becomes less important when one goes to distant galaxies where the Hubble redshift gives velocities much larger than any peculiar velocity (like in the example above: 15,000 km/sec is a good deal larger than expected peculiar velocities).
Another more subtle difficulty is that the expansion of space need not be uniform with time (in fact it is believed that it is not uniform). This means that Hubble's constant changes with time. Recall that as we look out through space we are looking back in time. Hence we are looking back to a time when Hubble's constant was different so we couldn't use our current value of Ho (even if we knew exactly what it was). In order to convert redshifts into accurate distances we require a complete model of the universe. This is one reason why we restricted our application of the Hubble law (above) to relatively nearby galaxies. We will put this issue to the side for the moment and return to it in our discussion of Cosmology.
Another thing to bear in mind is that the doppler formula we have been using to relate the redshift z to the velocity v is appropriate only for velocities much less than the speed of light (i.e., nearby galaxies). The formula z=v/c implies that you can't have redshifts greater than one because that would give you a velocity greater than the speed of light, something not permitted by the laws of physics. In fact, redshifts larger than 1 are possible, and are observed. For example, if an object has a velocity near the speed of light we have to use the "relativistic doppler shift formula"
(z+1)2 = (c+v)/(c-v)
which is derived from special relativity. You can see by the presence of the c-v in the denominator of the fraction that as v gets close to c the redshift becomes increasingly large. (z=c would yield an infinite redshift; remember the black hole where the redshift becomes infinite at the horizon where things are falling in at the speed of light.) Although we won't be making specific use of this formula in this course, it is a good idea to keep it mind the fact that redshifts greater than one imply velocities close to but not greater than the speed of light.
In fact, the redshifts of distant galaxies are not due to velocities in the ordinary sense. They are due to the expansion of space itself. We will take up this strange topic in more detail in the section on cosmology.
Here are some learning goals for the study of active galaxies:
 |
The Hubble Space Telescope Science Institute recently released a picture of galaxies in collision. Read the Press Release and see the picture. View a gallery of Gamma-Ray Astronomy Images. Take a look at the pictures of Radio Galaxies and Quasars for a view of the incredible images produced by radio telescope observations. Here are some Hubble Space Telescope images of active galaxies: |
Review Questions:
Much of this course to date has emphasized stars, and the gas from which stars form and to which they return. Galaxies are described in terms of the stars, gas and dust they contain. The observations of stars are most naturally made in the optical wavelengths of the electromagnetic spectrum. The Sun, an average star, has its emission peak in the center of the visible band. But, as we have discussed, there are other bands in the spectrum besides the visible, and as observations are made in these other wavelengths, many new and exciting discoveries are made.
 A prime example is found in the
invention of
the radio telescope and the resulting survey of the heavens in radio
wavelengths. One problem was that early radio telescopes did not give
very accurate positions in the sky. Radio sources were labeled
according to the constellation they were in but it was difficult to
identify a specific object for each radio source. One that was fairly
easy was the galactic center radio source: Sag A. (The designation
"Sag" indicates the area of the sky assigned to the constellation
Sagittarius, and the "A" indicates the most powerful radio source in
that constellation.) The center of our galaxy is one of the most
powerful radio sources in the sky, and this fact was quickly discovered
when radio telescopes were first put to use. Another strong radio
source in the constellation Cassiopeia (Cas A) was identified with a
supernova remnant. Many other powerful radio sources were also
discovered, but most of them could not be identified with known
objects. More accurate, that is, more highly resolved radio
observations become possible with the development of radio
interferometers composed of several separate radio telescopes linked
together electronically. It was then possible to find the "optical
counterpart." to the powerful radio sources. Astronomers were in for
several surprises. The first was the realization that many of the radio
sources corresponded to distant, but otherwise unremarkable galaxies.
The redshifts for these galaxies were often very large. The Cygnus A
radio source corresponds to a galaxy with a redshift of z=0.057. How
could it be that a fuzzy, distant galaxy that can barely be seen with
the largest telescopes, is one of the brightest radio objects in the
sky? This type of object is now known as a radio
galaxy.
A prime example is found in the
invention of
the radio telescope and the resulting survey of the heavens in radio
wavelengths. One problem was that early radio telescopes did not give
very accurate positions in the sky. Radio sources were labeled
according to the constellation they were in but it was difficult to
identify a specific object for each radio source. One that was fairly
easy was the galactic center radio source: Sag A. (The designation
"Sag" indicates the area of the sky assigned to the constellation
Sagittarius, and the "A" indicates the most powerful radio source in
that constellation.) The center of our galaxy is one of the most
powerful radio sources in the sky, and this fact was quickly discovered
when radio telescopes were first put to use. Another strong radio
source in the constellation Cassiopeia (Cas A) was identified with a
supernova remnant. Many other powerful radio sources were also
discovered, but most of them could not be identified with known
objects. More accurate, that is, more highly resolved radio
observations become possible with the development of radio
interferometers composed of several separate radio telescopes linked
together electronically. It was then possible to find the "optical
counterpart." to the powerful radio sources. Astronomers were in for
several surprises. The first was the realization that many of the radio
sources corresponded to distant, but otherwise unremarkable galaxies.
The redshifts for these galaxies were often very large. The Cygnus A
radio source corresponds to a galaxy with a redshift of z=0.057. How
could it be that a fuzzy, distant galaxy that can barely be seen with
the largest telescopes, is one of the brightest radio objects in the
sky? This type of object is now known as a radio
galaxy.
An even more surprising result was in store for another class of objects. The optical counterparts for these appeared to be stars: that is, they were unresolved point sources of optical light. However, when spectra of these stars were obtained they showed strange emission lines. These strange objects became known as quasi-stellar radio sources. This term has since been shortened to quasar. The breakthrough came when Maarten Schmidt at Caltech realized that a pattern of emission lines in the spectrum of a quasar matched the spacings of hydrogen emission lines; they were just out of place by a large amount corresponding to a redshift of 16 percent. The key realization was that the strange emission lines were ordinary emission lines redshifted by large amounts compared to what had been observed previously.
Once astronomers knew to identify the strange lines in quasars with large redshifts, quasars with much larger redshifts were quickly identified. Today thousands of quasars are known and many of these have redshifts larger than 1, and a few have redshifts greater than 4. Although many of the earliest detections were made in the radio band there is a class of radio-quiet quasars called quasi-stellar objects or QSOs. These have high redshifts like the radio-loud quasars, and are very luminous, but they do not have the radio emission. In fact the radio quiet QSOs significantly outnumber the radio-emitting quasars. NOTE: Although technically the term quasar refers to the radio loud objects it is a term that tends to be used casually by astronomers for both quasars and QSOs.
Quasars look like stars, that is, they are unresolved points of light. They don't look like stars, however, when you examine their spectra in detail. What does the spectrum of a typical quasar look like? First it has continuous emission, but the spectrum is not the thermal or blackbody type of spectrum that we associated with stars. Instead it is a nonthermal spectrum (which simply means not the blackbody spectrum given off by dense, hot matter) of the type expected for synchrotron emission. Recalling the discussion of this type of emission in the section on pulsars, this observation implies that quasars must have lots of energetic electrons and strong magnetic fields.
Next there are broad, strong emission lines in the quasar's spectrum. These emission lines are used to obtain the quasar's redshift. The emission lines provide evidence for hot, low density gas heated by strong source of ionizing radiation (e.g., UV radiation). Recall the emission nebula discussed earlier that were heated by O and B stars in their interiors. The implication is that there are gas clouds in quasars surrounding the central source of high energy synchrotron radiation. The emission lines indicate that quasars are composed of the same elements that make up other objects we have studied: hydrogen, helium, carbon, oxygen, nitrogen, etc. Finally, the fact that the emission lines are "broad," i.e., smeared out over a fairly wide range of wavelengths, means that the gas that is giving off those lines has a wide range of velocities (the smearing is due to doppler shifting), and that tells us that gas velocities in the quasar are on order of 1000 to 1500 km/sec.
Another property of quasars is that they sometimes are highly variable in their total luminosity. Many quasars show extreme variations in periods on order of a year. Some show rapid variations with periods of days or weeks. Recall the earlier discussion relating time variability to maximum size of an object, using the simple formula R=c dt. This formula simply states that if an object varies over an amount of time dt then the object can't be bigger than the distance light can travel in that time. If a quasar varies over a period of a few days that variation must be coming from a region that is smaller than a few light days across (barely bigger than our solar system). Even the quasars that vary in the period of a year must be doing so within a region less than a lightyear in diameter. Recalling that the nearest star to our solar system is 4 lightyears away it is clear that these sizes represent vary small regions on the galactic scale.
The small size of a quasar's emission region is all the more puzzling when one combines the redshift of the quasar with Hubble's law to obtain a distance, and then uses the apparent magnitude to get an absolute quasar magnitude: quasars are enormously powerful. A typical quasar produces 100 to 10,000 times as much luminosity as an entire spiral galaxy, or more than 1013 times the luminosity of our sun. The problem then is that quasars are emitting all this luminosity within a region that is only a few parsecs across!
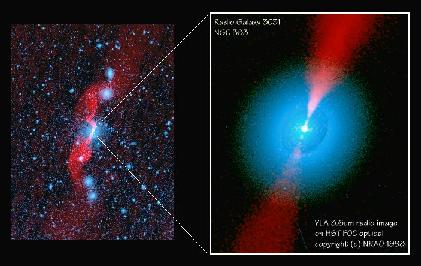 More evidence for the strange properties of
quasars comes from observations of some of the radio-loud quasars. In
about half of the radio quasars we see a concentration of radio
emission called a compact
radio source at the location of the quasar. In the other half one
also sees extended radio emission in the form of oppositely
directed radio
jets extending outwards for distances up to megaparsecs. As one
examines these jets on ever decreasing scales, they maintain their
integrity down to the parsec scale, supporting the picture that the
power in a quasar is all being generated in a very small region. (Note:
radio observations on very small scales are possible through the
technique of VLBI, Very Long Baseline Interferometry. This technique
uses radio telescopes around the world to make simultaneous
observations which can be combined to simulate a radio telescope with a
baseline equal to the size of the Earth. Resolution in a telescope goes
like the wavelength divided by the diameter of the telescope---see
chapter on telescopes for more details.) The jets terminate in regions
of diffuse radio emission called radio lobes. Presumably this
is where the jets run out of steam, terminating in a shock wave which
produces a hot spot. The radio emission in the jets is synchrotron,
meaning again that there are lots of energetic electrons and magnetic
fields in the jets.
More evidence for the strange properties of
quasars comes from observations of some of the radio-loud quasars. In
about half of the radio quasars we see a concentration of radio
emission called a compact
radio source at the location of the quasar. In the other half one
also sees extended radio emission in the form of oppositely
directed radio
jets extending outwards for distances up to megaparsecs. As one
examines these jets on ever decreasing scales, they maintain their
integrity down to the parsec scale, supporting the picture that the
power in a quasar is all being generated in a very small region. (Note:
radio observations on very small scales are possible through the
technique of VLBI, Very Long Baseline Interferometry. This technique
uses radio telescopes around the world to make simultaneous
observations which can be combined to simulate a radio telescope with a
baseline equal to the size of the Earth. Resolution in a telescope goes
like the wavelength divided by the diameter of the telescope---see
chapter on telescopes for more details.) The jets terminate in regions
of diffuse radio emission called radio lobes. Presumably this
is where the jets run out of steam, terminating in a shock wave which
produces a hot spot. The radio emission in the jets is synchrotron,
meaning again that there are lots of energetic electrons and magnetic
fields in the jets.
To summarize the properties of quasars: (1) they have a starlike appearance, (2) they have large redshifts. Combined with the Hubble law this implies great distances, and, judging by their apparent magnitudes, great luminosity. (3) Their continuum spectrum is dominated by nonthermal synchrotron-type radiation, and there are also broad emission lines. The doppler shifts of the emission lines indicate velocities on order of 1000 km/sec. (4) Variability on timescales of a year or so is common and some quasars show rapid variability on times ranging from days to weeks. (5) Some are strong radio emitters, and of those about half have radio jets.
How can we interpret these observations to form a model of a quasar? The observations imply tremendous energy coming from a very small region, nonthermal emission consistent with high energy electrons and strong magnetic fields, large mass as implied by the high velocity gas and Kepler's laws. The radio jets that are observed to stretch out over huge scales have a straight line appearance that implies a specific sense of direction associated with the central power source, a direction that has been maintained for millions of years.
Now let's try to see if these quasar phenomena could be explained somehow using stars. Consider a model that used a dense cluster of hot stars to power a quasar. First there would have to be a lot of them: even the hottest O stars produce only 104 solar luminosities and assuming the whole quasar emission came from them we would need 100 billion such stars. Those stars are also very massive so we would need to have about 1013 solar masses of stars within a one parsec radius. If you recall that a solar mass black hole would have a Schwarzschild radius of 3 km, then this much mass has a Schwarzschild radius of 3 x 1013 km which is just about equal to one parsec. This means we would have to push our supermassive star cluster together to nearly its Schwarzschild radius in order to get enough energy into a compact region. And even then one doesn't have the correct energetics: these stars would produce mainly UV radiation, not synchrotron. And how would a cluster of stars produce radio jets? There is no specific sense of direction implied by an essentially spherical cluster of stars.
The requirements of great energy within a small region point to a model that makes use of a black hole. Basically this model is a scaled-up version of the black hole in a binary system model that was used for Cygnus X-1. Now however we have a supermassive black hole, a black hole with a mass somewhere between a million and a billion solar masses. A hundred million solar mass black hole has a Schwarzschild radius comparable with the orbit of Mars. The accretion disk surrounding that black hole is huge by stellar standards: several times bigger than our solar system. And yet the whole thing fits comfortably within the parsec or so scale required by the observations. In a binary system the black hole's accretion disk is fed by mass overflow from the companion star through the Lagrange point in the Roche potential. The supermassive black hole doesn't have a companion star. Its accretion disk is fed by the host galaxy itself, from the interstellar medium and by the process of tidally ripping apart whole stars.
 Figure: Artist's conception of an accretion disk
and jet around a supermassive black hole in the core of an active
galaxy. (Greg Foss; PSC)
Figure: Artist's conception of an accretion disk
and jet around a supermassive black hole in the core of an active
galaxy. (Greg Foss; PSC)
How does the supermassive black hole produce all the required properties of something like a quasar? As the gas in the accretion disk spirals down towards the black hole, frictional forces cause the gas to heat up thereby releasing energy. The source of that energy is the fall down the gravitational field. Anything falling down in a gravitational field is picking up energy: jump off a building and you rapidly pick up speed, or energy of motion; when you hit the ground that energy of motion is dissipated into heat and broken bones! Because the black hole has such a powerful gravitational field, a great deal of energy is available. In fact the amount of energy is on order of 10 percent the energy in a mass m as given by Einstein's formula mc2. You may recall that nuclear reactions released less than one percent of mc2, so black holes can be much more efficient than stars in releasing energy from their fuel.
As we discussed in the section on black holes, black holes can only increase their mass with time (ignoring Hawking radiation which has an utterly negligable effect on massive black holes). Now since quasars occur at large redshift, they are present a long time ago, more than halfway back to the beginning of the universe. Hence those black holes that powered quasars must still be around. What are they up to today? To answer this we must broaden our discussion to the entire class of objects known as Active Galaxies. Active Galaxies are characterized by certain properties: (1) High Luminosity, (2) Nonthermal Spectra that do not look like the sum of many stellar spectra, (3) Most of the luminosity is in a region of the spectrum other than optical (e.g., radio, UV, Infrared), (4) bright, star-like nucleus, (5) strong emission lines (most), (6) rapid variability, and sometimes (7) radio jets. These properties were seen in the quasars and they are present in closer, otherwise normal galaxies, although at lower luminosity levels. Because the nonstellar activity seems to be concentrated in the center of the active galaxy, these objects are also known as Active Galactic Nuclei, or AGN.
One type of active galaxy we have already discussed is the Radio Galaxy. Radio galaxies are generally elliptical galaxies, they have a powerful compact radio source at their center, and often they have radio jets. Another type of active galaxy is the Seyfert Galaxy. Seyferts are spirals that have bright starlike nuclei. In fact, if one takes a picture of a Seyfert using a very short exposure all one sees is the compact nucleus and the Seyfert looks very much like a quasar, albeit at much lower redshift. This is very suggestive. Seyferts have strong emission lines, and the emission lines are very broad, implying velocities from 500 to 4000 km/sec. Seyferts are classified into two types based on the width of their emission lines. Seyferts with very broad Hydrogen emission lines are called Type I, and Seyferts with more narrow Hydrogen emission lines are called Type II. Many Seyferts also have compact radio sources at their centers.
Figure 26-7 shows a Seyfert galaxy. On long exposures the spiral galaxy is visible along with the point-like nucleus. If one takes a short photographic exposure, only the nucleus is seen.
Another type of active galaxy is the BL Lac object, named after the first one of these things found (it was in the constellation Lacerta). These are also sometimes called blazars. BL Lac objects have the following properties: (1) very rapid (day to day) variability by large percentages in total luminosity, (2) no emission lines, (3) strong nonthermal radiation, (4) starlike appearance (in fact when first discovered, BL Lac was thought to be an unusual variable star). Studies begun in the '70s found the BL Lac is surrounded by "fuzz," that is very faint light that has a spectrum very much like an elliptical galaxy. The idea that has developed is that a BL Lac object is a radio galaxy where we are looking down the jet into the very heart of the system, right into the central engine. Since we are looking right along the jet we see very rapid, highly luminous radiation: like looking right into a searchlight it is beamed at us.
Can we construct some sort of unified model out of all this? Astronomers have been attempting such a thing, with mixed success. At the moment the "standard picture" goes something like this: Notice that in terms of redshift (and hence lookback time), the quasars have the largest redshifts, followed by the BL Lacs, followed by the Seyferts and the radio galaxies. This is also the general progression in terms of luminosity. When quasars are studied with telescopes capable of detecting very faint light some of them show a faint "fuzz" around them, just like the BL Lacs. Other observations show quasars located within clusters of galaxies with the same redshift. If we look at Seyferts with very short exposures they look like quasars because the regular galaxy part is underexposed compared to the nucleus. All of these observations suggest that quasars are active galaxies with particularly active nuclei. Perhaps today's active galaxies used to be quasars. Back when the galaxies were very young they had more gas than they do today and this gas could have fed a supermassive black hole at a great rate. This would account for the high luminosity of the quasars. Today the galaxies are still there, but the rate at which gas is fed into the accretion disk surrounding the black hole is much reduced and so the central engine is less active and one has one or the other of the types of active galaxies.
If this unified picture is correct, then we should be able to detect the leftover supermassive black holes in nearby galaxies. Recent photos from the Hubble space telescope show a disk-like structure about 100 pc across in a nearby radio galaxy that has a jet. That picture is certainly consistent with the supermassive black hole model. Another test of the model is to study rotation curves near the centers of nearby galaxies. If there is a supermassive black hole in the center then the velocity of orbiting gas and stars should rapidly increase (according to Kepler's law) the closer they are to the center. In the absence of such a huge compact mass at the center the orbital velocities should remain flat and then go to zero at the center. So big high velocity spikes at the centers of galaxies would be indicative of very massive compact bodies. Hubble space telescope may be able to help with this sort of observation as well (particularly when its optics get fixed). The key thing will be to get high accuracy spectra on small scales (parsec) near the center of the galaxy.
 Figure: A Hubble Space
Telescope image of a quasar reveals the presence of a galaxy
surrounding the quasar's bright nucleus.
Figure: A Hubble Space
Telescope image of a quasar reveals the presence of a galaxy
surrounding the quasar's bright nucleus.
Here are some learning goals for the study of Cosmology:
 |
Cosmology is the subject of the entire semester in my spring course Introduction to Cosmology. This course is a quite suitable follow-on to Astro 124 for those of you who have enjoyed this course and would like to learn more about the Big Bang. It is also the subject of a textbook Foundations of Modern Cosmology. This book will be the text for Astro 348 next semester. Go to the book link for further information, and lots of cosmology-related links. Here are a couple of web pages by John Dubinski at the Canadian Institute for Theoretical Astronomy that discuss computer simulations of galaxy mergers, along with some neat MPEG movies. See The Merger of the Milky Way and Andromeda and The Antenna Galaxy. |
Throughout this course we have been considering things on ever increasing scales. Now we wish to think about the universe as a whole, and about the galaxies and clusters of galaxies that make up the universe. We will also begin to talk about how the universe has evolved over its lifetime (estimated to be 15-20 billion years). We are aided in our attempts to comprehend the history of the universe by the fact that as we look out into space, to greater and greater distances, we are looking back in time. Light has a finite travel time and that means when we look out we are looking back and seeing things how they used to be, not how things are now. For example, alpha Centari is 4 light years away so it takes 4 years for light to reach us from there. The further out one goes, the larger the lookback time. The light from a galaxy that is one megaparsec away takes about 3 million years to reach us. Three million years isn't very much time in terms of galactic evolution, but we can see objects, known as quasars, for whom the lookback time is substantial compared to the age of the universe. Hence, as we look out into space we can, in principle, see the history of the universe laid out before us. From this we can construct cosmological models.
In order to make any progress at all we need to adopt an overriding philosophical principle that can guide our development of a model of the universe. This principle is known as the Cosmological Principle. The cosmological principle holds that the universe is the same in all places (a property known as homogeneity) and looks the same in all directions (a property known as isotropy). This principle refers to properties on the largest scales. Obviously the Earth is a special place (we live here after all) that is different from other places. The Milky Way galaxy is a flattened disk so there is a special direction (in the plane of the disk versus out of the disk). However, on the grand scale, the scale where the galaxies are reduced to points spread out over billions of parsecs, the cosmological principle holds. Consequences of the cosmological principle are that the distant galaxies have the same laws of physics as we observe here on Earth, they have the same types of atoms and molecules, any observations made by creatures in other galaxies should lead to the same conclusions as we reach by similar observations. You can see how the cosmological principle is a very powerful assumption. By adopting the cosmological principle we can assume that our corner of the universe is representative of the whole universe, and by carrying out experiments here in our terrestrial laboratories we are learning about remote galaxies that we can never hope to visit directly.
We would note, as an aside, that the cosmological principle has been slow in coming to the thinking of humanity. Early cosmologies (e.g., the ancient Greeks, or Europe before the time of Newton) place the Earth at the center of everything. The ``Copernican Revolution'' was the adoption of the idea of Copernicus that the Sun was the center of the solar system (actually Copernicus still thought the Sun was the center of the universe), so the notion that we do not occupy a special location in the universe is often referred to as the Copernican Principle. Even in this century there was debate as to whether or not the Sun was near the center of the Milky Way, and whether or not the Milky Way was the biggest of all galaxies and at the center of the system of ``nebulae.'' We have very gradually come to realize that the Sun is an average star, located at the edge of an average galaxy, inside a small group of galaxies at the outskirts of a much bigger group of galaxies (the Virgo cluster) which is a small cluster of galaxies compared to really big clusters of galaxies....
How are galaxies arranged? In our immediate vicinity there are a number of galaxies that make up our "local group." This consists of about 30 galaxies all within about a megaparsec of each other. There are three massive members consisting of the milky way, M31 (Andromeda) and M33, an Sc type. The rest are dwarf ellipticals and irregulars (like the LMC). (See Figure 27-3 for a diagram of the Local Group.)
In general galaxies are often found in groups or clusters. Clusters of galaxies themselves tend to cluster into superclusters. An example is the Virgo cluster of galaxies which is relatively nearby (20 Mpc), about 4 Mpc in diameter and containing around 2000 galaxies, most of which are dwarves. Another important cluster is the Coma cluster. It lies at a distance of about 100 Mpc and it contain perhaps as many as 10,000 galaxies spread out over at least 7 Mpc of space. There are many clusters of galaxies, most of which are considerably smaller than the Coma cluster. The astronomer George Abell compiled a catalogue of 2712 galaxy clusters (called, naturally enough, Abell clusters). He created two groups for the clusters (astronomers are always breaking things up into groups), the regular and irregular galaxy clusters. Regular clusters are spherically distributed and tend to have a high concentration of galaxies in their center. They tend to have lots (thousands) of galaxies and to have many bright E0 and S0 galaxies. For example, the Coma cluster is a regular cluster and only 15 percent of the visible galaxies are spirals or irregulars. Irregular Clusters are not as centrally condensed, nor are they so spherical in shape. There are often subcluster concentrations, and the total number of galaxies is much smaller. The local group is an example of an irregular cluster, as is the Virgo cluster.
An important general question about galaxies and clusters of galaxies is how they group themselves on the biggest scales. Observations of enormous numbers of galaxies seem to indicate that there are large regions that are more or less empty of galaxies; these are called voids. Other areas contain galaxy superclusters. Some regions appear as if they have long filaments or sheets of galaxys stretching across vast expanses of the universe. These things all provide clues as to the overall structure of the universe, and the way that the galaxies formed in the early stages of the universe. We will return to this large scale structure question in our discussion of cosmology.
 FIGURE: One way to
approach the question of the large scale structure of the universe is
with surveys of galaxies. One needs to obtain their positions on the
sky and their redshift (which, through the Hubble Law, provides a
measure of their distance from us). One example of such a project is
the Las Campanas Redshift Survey. Data from this survey is seen here.
This survey consists of 26418 galaxies for which redshifts have been
obtained. The plot shown here is the redshift distribution of these
galaxies, and it reveals many repetitions of empty regions, or voids,
sharply bounded by large walls of galaxies.
FIGURE: One way to
approach the question of the large scale structure of the universe is
with surveys of galaxies. One needs to obtain their positions on the
sky and their redshift (which, through the Hubble Law, provides a
measure of their distance from us). One example of such a project is
the Las Campanas Redshift Survey. Data from this survey is seen here.
This survey consists of 26418 galaxies for which redshifts have been
obtained. The plot shown here is the redshift distribution of these
galaxies, and it reveals many repetitions of empty regions, or voids,
sharply bounded by large walls of galaxies.
Recall in the discussion of the Milky Way galaxy that the rotation curve suggested that there was considerable mass present outside the disk of the galaxy. When rotation curves are obtained for external galaxies they reveal this same property: the rotation velocity does not drop off as one gets out to the edge of the galaxy. As before it implies that there is considerable nonluminous, or dark matter surrounding the galaxy. One can carry out a similar analysis for entire clusters. Galaxies within clusters have orbital speeds as they move about and this in turn implies a total mass for the cluster. The difficulty is that the total mass obtained by this method is larger by about a factor of 10 than the mass one gets by counting up the stars in the galaxies. Another piece of evidence is the detection of hot, X-ray emitting gas coming from the centers of some rich clusters. Recall that high temperature in a gas implies that the particles making up that gas are moving at high speed. If such high speed particles are to be retained in the cluster, and not disperse into intergalactic space, there must be strong gravity to hold onto the gas. The amount of mass needed to produce such gravity is larger than that associated with the luminous components of the visible galaxies. Again this implies that most of the matter in galaxy clusters is nonluminous. This is the dark matter or missing matter problem. What is the source of this unseen matter that is affecting the orbits of the galaxies and binding the cluster together? This is a major unsolved problem in astronomy.
Gravity is the force that dominates events on the huge scales of galactic and intergalactic space. It is gravity that binds the individual galaxy together, and gravity that causes galaxies to clump into clusters. As we shall see when we take up cosmology, gavity controls the very evolution and fate of the universe itself. Here we will consider how gravity affects individual galaxies in collision.
 For years following the discovery that
external galaxies existed, they were regarded as serene islands, living
essential in isolation from one another. If it occasionally appeared
that a galaxy was colliding with another this was considered anomalous.
However, as astronomers began to wonder how galaxies evolved and
changed with time, it was realized that one way they might change
dramatically would be through collisions.
For years following the discovery that
external galaxies existed, they were regarded as serene islands, living
essential in isolation from one another. If it occasionally appeared
that a galaxy was colliding with another this was considered anomalous.
However, as astronomers began to wonder how galaxies evolved and
changed with time, it was realized that one way they might change
dramatically would be through collisions.
Galaxies in clusters move through the cluster on orbits that pass through or near the center of the cluster. This leads to the possibility of galaxy collisions. Galaxies are mostly empty space so when they collide their stars can pass by each other without any problem. However the gravitational forces of one galaxy on the other have a significant affect. Near encounters can generate strong spiral features in galactic disks, and large bars in bulges. If the galaxies come close enough to each other they can merge and for one galaxy. If a big galaxy lives in the center of a cluster then it can merge with many other smaller galaxies and grow to enormous size. This process is known as galactic cannibalism and may account for the huge size and mass of the central galaxies in big galaxy clusters.
Even our own Milky Way has a possible collision in its future. The Andromeda galaxy is approaching us with a speed of about 50 km/sec. We don't know whether we will have a head on collision or just a close passage.
What would a collision be like? Well it doesn't involve collisions of individual stars. Compared to the vastness of space, stars are tiny, insignificant points. What is really colliding are the gravitational fields of the two galaxies. The orbits of the gas and stars making up a galaxy are determined by the gravity of the galaxy and the presence of another, nearby galaxy will substantially alter that gravitational field. This will result in substantially altered orbits for the stars and may result in the merger of the interacting galaxies.
 When galaxies merge lots of interesting
things may happen. Mergers result in interstellar gas being compressed
and shocked (although the stars don't collide, clouds of gas are
sufficently wide to do so). Such collisions trigger extensive star
formation. This can result in something known as a starburst galaxy.
The burst of star formation uses up much of the gas in the merging
galaxies, and the release of energy from the resulting stars (and their
subsequent supernova explosions) drives off much of the rest. It is
possible that this is the process that leads to the formation of gas
poor elliptical galaxies. A merger may also result in the formation of
globular clusters. The recent HST observations of colliding galaxies
seem to bear this expectation out.
When galaxies merge lots of interesting
things may happen. Mergers result in interstellar gas being compressed
and shocked (although the stars don't collide, clouds of gas are
sufficently wide to do so). Such collisions trigger extensive star
formation. This can result in something known as a starburst galaxy.
The burst of star formation uses up much of the gas in the merging
galaxies, and the release of energy from the resulting stars (and their
subsequent supernova explosions) drives off much of the rest. It is
possible that this is the process that leads to the formation of gas
poor elliptical galaxies. A merger may also result in the formation of
globular clusters. The recent HST observations of colliding galaxies
seem to bear this expectation out.
Let's consider how we might expect galaxies to change over time. This is the subject of galaxy evolution, and it is a difficult one for several reasons. To start, we recognize that most of the light in a galaxy comes from stars so the appearance of a given galaxy will depend upon the types of stars out of which it is composed. Recall the HR diagram; the massive stars make up the highly luminous blue O and B type stars. Less massive stars have much lower luminosity and redder colors from their lower temperatures. There are many more low mass stars as compared to high mass stars, but the high mass O and B stars are so very luminous that when they are present their luminosity tends to dominate and the galaxies colors tend towards blue. Massive stars evolve relatively quickly, however, and after they have left the main sequence and ended their lives as supernova we are left with the redder, low luminosity, low mass stars. So a galaxy containing older stars tends to have redder colors. Elliptical galaxies are very reddish in color, implying that they mainly contain old stars. Spiral galaxies have old stars in their bulges and in their halos (globular clusters for example) but the disk contains hot young stars so the disks of spirals are blue. As we discussed before, the disks of spirals contain considerable dust and gas. The spirals themselves seem to be made up of young hot stars created, quite probably, by spiral density waves moving through the disk.
Comparing the shapes of ellipticals and spirals leads us to suggest the following picture: A galaxy begins as a huge cloud of gas, collapsing under its own gravitational force. If star formation took place early on in this process then the stars would be formed distributed throughout this primordial, generally spherical volume of gas. If stars do not form immediately then the gas will settle down into a disk that rotates primarily along one axis. The difference between these two states, the spherical system and the disk is due to the fact that gas collides with itself and dissipates energy while stars do not collide. A bunch of gas therefore will become increasingly compressed and compacted until it settles into a rotating disk (rotating because of whatever initial spin it had, and conservation of angular momentum.) When stars form they do not collide and so can't disspate the energy of their motion. So if stars form in a big spherical cloud the stars will remain in a big spherical cloud, moving around inside the cloud in long elliptical orbits. The general picture is that ellipticals had their star formation early and the spirals had their star formation late. This picture is also consistent with the fact that the spherical components of spirals, namely the bulge and the halo, contain old stars, formed long ago.
Don't forget the "dark matter." Most of the mass of a galaxy is apparently not in the visible stars and gas. What is this mysterious mass? How does it contribute to the galaxy formation process? These are all areas of active speculation and research at present.
It should be noted that the process of galaxy formation is still a very mysterious one. No one knows quite for sure how it works. We have clues, like the ages of the stars in the various morphological types, and the fact that ellipticals are found preferentially in clusters as compared to spirals. Does this latter fact imply that something about the presence of lots of other galaxies initiates more vigorous star formation in the forming protogalaxy? This brings up the question: Which came first, galaxies or clusters of galaxies? This is the issue of whether structure formed by a ``top down'' or a ``bottom-up' process. In the top-down scenario, the big structures form first (the clusters and superclusters) and then fragment into separate galaxies. In the bottom-up scenario galaxies form first and are then drawn together by their mutual graviational attraction to create clusters and superclusters. The quasars and the associated high redshift galaxies indicate that individual galaxy formation started fairly early on in the history of the universe, and this currently favors the bottom-up scenario.
Here are some review questions:
Cosmology is the study of the origin and evolution of the whole universe and all it contains. The universe is the sum of all that is physical, including all matter and energy, space and time, the laws of nature, and all that can be affected by or can potentially affect us or be visible to us. In carrying out cosmological studies we must be well aware that we are not really describing the whole universe. The universe is too vast and unknowable for us to do that. All we are trying to do is to obtain models of the universe that will reflect our best understanding of the universe at this moment. There are many possible models and the best we can do is compare the predictions of those models to what we actually observe.
The best current cosmological model is the expanding universe Big Bang model. Our goal in this section is to understand what this model means, what its predictions are, and what problems or unanswered questions remain.
The first cosmological model that we wish to consider is the one formulated by Isaac Newton. Newton, as you will recall, was the first to find mathematical relationships for the laws of mechanics, that is the rules that govern motion. In particular Newton's law F=ma describes how force produces an acceleration in a body of mass m, and Newton's gravity law describes the force due to gravity between two massive bodies. In principle then, Newton reasoned, he could describe the entire universe in terms of the laws of motion and the force of gravity. Consider a universe consisting of stars moving about. If you knew their initial velocities, positions and masses, you could determine the gravitational force on each star due to every other star, compute the accelerations that result, adjust the stars' velocities and positions, recompute the new forces, and so forth. It is a completely deterministic (and clockwork) description of the universe. Newton realized that if the universe contained only a small finite cluster of stars, that cluster would eventually collapse due to gravitational forces. He reasoned that this required the universe to be infinite with stars distributed uniformly in all directions. The total gravitational force at any one location would thereby more or less be cancelled out. So Newton envisioned a uniform, static universe of infinite size and infinite duration. (In considering Newton's model we may wish to update it by replacing the uniform distribution of stars with a uniform distribution of galaxies.)
Newton's theory of mechanics and gravity was the accepted theory at the beginning of the twentieth century. However, it was to be replaced by a new and more complete theory developed by Albert Einstein. Einstein's theory of general relativity deals with the force of gravity and how masses affect the geometry (shape) of space and time. Space and time were now part of larger concept known as space-time. This is different from Newton's idea of space and time being separate and immutable. The geometry of space-time determines how things move through space and time and mass in turn determines the geometry of space-time. The analogy usually invoked is that of ball bearings on a rubber sheet. The balls move about on the sheet as determined by the shape of the sheet, but the balls themselves bend the sheet and affect its shape. The theory of general relativity became the description of how the force of gravity is determined and how it determines motions.
Now Einstein realized that the presence of matter in the whole universe could curve the overall shape of space in the universe. That is he went from applying his theory to the orbits of planets in the solar system to the structure of the universe as a whole. What he developed from this idea was a universe that was finite in size but without any edges or boundaries. It was a spherical universe. What does this mean? The surface of an ordinary sphere (like the Earth, for example) is a two dimensional surface that is curved. It has no edges but is finite in extent. (Christopher Columbus did not sail off the edge of the Earth, but the Earth does not stretch on forever in all directions. Go long enough in any one direction and you will return to your starting location.) The conceptual leap that is required is to imagine a sphere in a higher dimension, one for which all three dimensions are curved resulting in a finite sized volume but without edges. In a universe like this you would head off in one direction, and without ever making a turn wind up back where you started from. You could send off a light beam in a certain direction then turn around and see the light beam come back to you from the opposite direction (after waiting the required time for the light to go clear through the universe!). If this seems strange recall that we have already encountered a spot where you could ``see the back of your head'' by looking off into a direction. This was close to a black hole where the effects of gravity are so strong as to curve light beams into a circular orbit. This sort of idea would hold for the universe as well: if it contains enough matter it curves space in upon itself into a finite total volume. This is an admittedly nonintuitive concept.
Now back to Einstein: his goal was to construct a nice self-contained model with curved space that was consistent with the cosmological principle and also static. What he found, however, was that if he left his model to its own devices it would not remain static but would collapse down upon itself. Basically if there is enough matter in the universe to close space into a sphere, that is to close space in upon itself, then there is enough matter to make strong gravitational forces that would pull all that matter together. We have encountered something like this before as well: inside the horizon of a black hole where collapse to a singularity is inevitable because of the gravitational force. Einstein tried to fudge his model by adding another term, designated the ``lambda'' force, to create a repulsive force to counteract the gravity. But it turned out that this didn't work either because if the two forces weren't always perfectly in balance the model would either expand forever (repulsive force wins) or contract to a singularity (gravity wins). Einstein was unable to get a static model that worked. What Einstein didn't realize was that his model was predicting what Hubble was to discover: the universe is not static at all but is expanding!
The discovery of the expanding universe was Edwin Hubble's preeminent contribution to modern cosmology, and as we have already discussed, he accomplished it by collecting data on the distances to galaxies along with their redshifts. It was already known at this time that, for whatever reason, most galaxies showed a redshift, that is they were moving away from us. This had first been noticed by V. M. Slipher who found that 11 out of 15 ``nebula'' had noticeable redshifts. In the 1920 Hubble and Milton Humason took spectra for many galaxies and found that almost all had significant redshifts. What they found was that one could almost draw a straight line on a graph of redshift versus distance, that is redshift equals distance times a constant. Today we refer to the constant as ``Hubble's Constant.'' This Hubble constant (H) is one of the most important cosmological parameters. As we shall see it provides a direct measure of how rapidly the universe is expanding, and an estimate of the age of the universe.
The first point to realize is that the observation of redshifts in galaxies does not mean that somehow all the galaxies are moving at high speed away from us and that we are at the center of some big explosion. This would not be consistent with the cosmological principle for it would place us at a preferred or special location, i.e., at the center. In fact the Hubble law is not telling us that galaxies are moving away from us, but that all of space in the universe is expanding and this expansion makes the distances between all the galaxies increase with time. The galaxies seem to move apart, and observers in each galaxy see the other galaxies moving away from them. All observers will see themselves to be apparently at the center of the expansion. Wait, you may ask, if space time is expanding why doesn't the galaxy expand as well, and everything scales up and hence no expansion is determinable. The answer comes from remembering that in cosmology we look at things on the largest scale. The expansion of space is determined by the average gravitational field of the universe. A galaxy, a star, the Earth, you, all reside in local gravitational fields caused by the presence of significant mass. The galaxies themselves do not expand because their local space is held together by the mass (and hence the gravitational force) of the galaxy itself. As an analogy imagine an expanding rubber sheet with ball bearings on it. The rubber sheet may expand but the ball bearings remain and the little dimples that they make in the sheet do not scale up.
By the cosmological principle every point in the universe sees remote galaxies expanding away from it according to the Hubble law. Also there is no dependence on any direction: the expansion proceeds equally in all directions. In fact the Hubble law, in which expansion velocity is simply proportional to distance, is the only expansion law that will make expansion seem the same no matter where you are in the universe. Note however that the rate of expansion (as determined by the Hubble constant H) can change with time. As we shall discuss momentarily, the universe is probably expanding at a slower rate today than it was earlier in its history.
Why does the expansion of the universe translate into a cosmological redshift? Consider a distant quasar. Recall that because of the lookback time effect we are seeing the quasar as it was many billions of years ago when the universe was younger. Since the universe is getting bigger with time, it follows that it must have been smaller long ago. When the quasar emitted some light that light had an unshifted wavelength of lambdaq. Now as that light has traveled across the universe it has been stretched out by the expansion of space and the wavelength has similarly stretched out to the longer value that we observe it today. The ratio of today's wavelength to the emitted wavelength is the ratio of the size of the universe today compared with then. The definition of redshift is
z = (lambda - lambdaq) / lambdaq = (lambda/lambdaq) -1
which means that the ratio of the size of the universe now to then is lambda/lambdaq = z+1. This is known as the expansion factor. For example, the universe has doubled in size since the time of redshift of 1, and increased 4 times since a redshift of 3. The expansion factor indicates an increase in linear dimensions. A volume is a length cubed, so volumes increase as the expansion factor cubed. This means that at a redshift of 1 the universe was 8 times as dense as it is today, and 64 times as dense as it is today at a redshift of 3.
Recognizing how densities and sizes go with redshift we realize that if we go back to a very remote time the universe must have been very hot and dense indeed. The question that occurred to astronomers in the 40's and 50's was are there any observable consequences from this hot and dense time? Back then, when the universe was filled with high temperature material it would have emitted light according to a high temperature blackbody. Things were so hot and dense that the universe resembled the interior of a star with ionized gas everywhere and photons of light scattering off of the electrons in the gas. When the universe cooled to a temperature of about 3000 K the electrons would have recombined with the protons forming hydrogen atoms (becoming un-ionized) and at that time the blackbody photons would no longer have interacted with the matter. After this the photons would simply stream through space, being redshifted.
In the 1960's Arno Penzias and Robert Wilson of Bell Labs were working with a microwave antenna for communications research when they found that no matter where they pointed their antenna at the sky they detected a faint background noise. After eliminating all possible sources of detector or experimental noise they concluded that they were picking up a genuine microwave signal from the sky. In fact, what they detected was the left over photons from the hot dense state in the early universe. This has become known as the Cosmic Background Radiation. These light particles had cooled down now so that their blackbody spectrum peaked in the microwave radio portion of the spectrum. This corresponds to a temperature of 3K. Since for blackbody radiation the peak wavelength goes like the temperature, we can conclude that the temperature goes down like the expansion factor which means that the photons detected in the microwave background radiation came to us from a time when the temperature was 3000K, or at a redshift of about z=1000! The observation of the microwave background radiation provides direct evidence that the universe was once in a hot dense state and is one of the fundamental experimental results that supports the Big Bang theory. This theory of cosmology simply states that the present universe has expanded out of a primordial state of high temperature and great density.
 Microwave radio detections from the
ground are rather difficult. In fact, near the peak of a blackbody
spectrum for a blackbody of 3K the atmosphere is opaque to the
microwave radiation. Hence, although the early measurements established
the existence of this cosmic background, there were several unanswered
questions. First, just how close to a perfect blackbody is the
spectrum? There might be features in the spectrum that would make it
more complicated. What was the precise temperature of the blackbody?
Did it vary over the sky, i.e., were there hot spots and cold spots on
the sky? In fact we know that there is one large variation. Because the
Earth and the Sun and the Milky Way are moving through space there is
an overall blueshift in the direction toward which we are moving and a
redshift in the direction from which we come. But these are just the
usual doppler shifts resulting from our motion. Are there small scale
variations that would correspond to hot and cold spots in the early
universe. The answers to these questions had to wait for a space
mission, and in 1989 the COBE (Cosmic Background Explorer) satellite
was launched to observe in the microwave region of the spectrum from
above the Earth's atmosphere. There were several important results from
this experiment. First the spectrum is as close to a perfect blackbody
as we can measure, and it has a temperature of 2.735K (with a small
uncertainty in the last decimal place). Second there are very small
variations throughout the sky of this temperature (at a level of about
one part in a million). These caused great excitement when announced
for they constitute the first direct evidence of emerging structure at
the very earliest observable times in the universe.
Microwave radio detections from the
ground are rather difficult. In fact, near the peak of a blackbody
spectrum for a blackbody of 3K the atmosphere is opaque to the
microwave radiation. Hence, although the early measurements established
the existence of this cosmic background, there were several unanswered
questions. First, just how close to a perfect blackbody is the
spectrum? There might be features in the spectrum that would make it
more complicated. What was the precise temperature of the blackbody?
Did it vary over the sky, i.e., were there hot spots and cold spots on
the sky? In fact we know that there is one large variation. Because the
Earth and the Sun and the Milky Way are moving through space there is
an overall blueshift in the direction toward which we are moving and a
redshift in the direction from which we come. But these are just the
usual doppler shifts resulting from our motion. Are there small scale
variations that would correspond to hot and cold spots in the early
universe. The answers to these questions had to wait for a space
mission, and in 1989 the COBE (Cosmic Background Explorer) satellite
was launched to observe in the microwave region of the spectrum from
above the Earth's atmosphere. There were several important results from
this experiment. First the spectrum is as close to a perfect blackbody
as we can measure, and it has a temperature of 2.735K (with a small
uncertainty in the last decimal place). Second there are very small
variations throughout the sky of this temperature (at a level of about
one part in a million). These caused great excitement when announced
for they constitute the first direct evidence of emerging structure at
the very earliest observable times in the universe.
Just how long ago was this time of emerging structure and background radiation? We can get an estimate of the age of the universe by using the Hubble constant. The Hubble constant is like a velocity of expansion. Just as you can use a velocity plus a distance traveled to estimate the time you have been traveling, one can use the present-day Hubble constant to estimate how long the universe has been expanding. Example: you are traveling down the highway at 50 mph. You have come a distance of 75 miles. Therefore you have been traveling for 1.5 hours. A possible source of error: what if you have changed speed while you have been traveling? In the case of the Hubble constant we have to use today's value and it is quite likely that the universe was expanding faster in the past. However, proceeding with what we have note that the Hubble constant has units of inverse time. The density of matter necessary to bring the universe to a halt is known as the critical density. We will write this as rhocrit. The critical density is obtained from theoretical calculations and it depends on the Hubble constant (the faster we are expanding the larger the density required to stop that expansion). What we observe is the density of the universe at the present time and this is called rhoo. Now we need to compare rhoo to rhocrit. If the universe is denser than this critical density it will eventually stop expanding and recollapse. This is known as a closed universe. If the universe is less dense than the critical density then the universe will expand forever. This is an open universe. Astronomers define the ratio of the present density to the critical density Omega. Hence open models have Omega < 1 and closed models have Omega > 1.
Figure: Three possible cosmological models. Plotted is the "scale factor" of the universe versus time. Models with density less than the critical density are open and expand forever. These are labeled k=-1 (hyperbolic geometry) and k=0 (flat geometry). Models with density greater than the critical density will recollapse. This model is labeled k=+1 (spherical geometry).
In between the open and closed model is the very special model Omega =1. In this model, the universe has just enough matter to stop expanding just when time reaches infinity, that is it is coming to a stop but it is going to take an infinite time to do it. (In contrast the open model isn't going to come to a stop even after an infinite amount of time). It is called the flat universe because of its overall geometry. Closed universes have the geometry of a sphere, as we discussed for the Einstein universe. As Einstein found, spherical universes, left to their own devices, will recollapse. There is enough gravity to warp space into a closed sphere, and then to collapse that sphere back down to a singularity. The Omega = 1 universe is no longer spherical, but extends to infinity and has the usual flat geometry familiar from high school geometry courses (i.e., the radius of circles is 2 pi, the interior angles of a triangle sum to 180 degrees, etc). If the universe is open then it has another kind of geometry that goes by the name of hyperspherical. This is a geometry that is ``bigger'' than the flat geometry. For example, circles have a larger circumference than 2 pi.
Figure: The three possible geometries for cosmological models. Models with density greater than the critical density are spherical. Models with exactly the critical density are flat. Models with density less than the critical density are hyperbolic.
Now let's discuss the consequences of these various cosmological models and how we might distinguish between them and determine whether we live in an open or closed universe. The most obvious thing to do would be to measure the mass of the universe. Count the number of galaxies in some large, representative spatial volume, compute the mass of all their stars and gas, take that total mass and divide by the volume and from that determine the average density of matter in that volume and, by extension, in the universe. If we do that we find that the density of mass we can see is smaller than the critical density by a factor of 10-100. That would imply that Omega = 0.1-0.01 and that the universe is open. However, there might be mass that we aren't seeing. We have discussed this possibility previously when we talked about the ``missing mass'' or dark matter implied by galaxy rotation curves. If there is a lot of this dark matter, the density of the universe could be much larger than what we can see at present. Maybe the universe could be closed after all. The missing mass would have to be in the form of some unknown particles, or massive neutrinos, or some such; something that contributes mass but no light. If the universe were closed by such particles that would imply that the universe is mostly composed of those things; ordinary matter would be in the minority.
| Model | Geometry | k | Omega | Age | Fate | |
|---|---|---|---|---|---|---|
| Closed | Spherical | +1 | >1 | to < 2/3 tH | Recollapse | |
| Critical | Flat | 0 | =1 | to = 2/3 tH | Expand forever | |
| Open | Hyperbolic | -1 | <1 | 0 < to < 2/3 tH | Expand forever |
Another way to distinguish between models is to look at very distant galaxies and see if they can provide clues as to the overall geometry of the universe. In flat geometry the surface area of a sphere is 4 pi R2. If you consider all the galaxies at some distance R, and you assume that they are spread out evenly over space at that distance, then the number of galaxies you see at some distance increases like the surface area of a sphere in flat space, i.e., as R2. If the geometry isn't flat then the number of galaxies might increase faster than R2 (open universe) or slower than R2 (closed universe). If you like, there is ``more space'' available to fill up with galaxies in the open universe, and less in the closed universe. So counts of the number of galaxies as a function of distance could reveal what kind of universe we live in. The main trouble with this is that in order for the geometry effects to become noticeable you have to go out a large distance (redshifts greater than 1), and galaxies at that distance are too faint to be easily seen with current ground based telescopes.
Yet another test comes from the age of the universe. First we need to determine Hubble's constant. Then we can get a Hubble time which in turn sets an upper limit on the age of the universe. The age of the universe is equal to the Hubble time only if the universe has not decelerated since the big bang. The universe decelerates due to the gravitational forces between matter, hence the more massive the universe the faster it decelerates, and the less time back to the big bang. Hence the closed models have lived a shorter time to the present than the open models.
Figure: The Hubble time is the amount of time one predicts by projecting back assuming the universe has always been expanding at its current rate. If the universe used to be expanding much faster then the Hubble time overestimates the age of the universe. If the universe is expanding faster today than it used to be, the Hubble time underestimates the true age of the universe.
Open models can have an age for the universe ranging from the Hubble time down to 2/3 the Hubble time. The flat model has an age exactly equal to 2/3 the Hubble time, and the closed models have ages less than this. Now the Hubble time for Ho = 50 km/sec/Mpc is 20 billion years. The flat model therefore has an age of 13.3 billion years. Now suppose that we found a star that we knew from stellar evolution theory to be 14 billion years old. That would pretty much rule out the closed models and the flat model. The only model where the universe is older than that star would be an open model (for this value of the Hubble constant). Notice that if the Hubble constant is 100 km/sec/Mpc, then the flat model would have an age of 6.7 billion years. Given the fact that the Sun is 5 billion years old that would be very hard to reconcile with such a universe. Since the computed ages of the oldest globular clusters range from 8 to 15 billion years (there is some uncertainty within this range), we can see why cosmologists tend to prefer the lower value of the Hubble constant.
How does the universe end in these various models? If the universe is closed then eventually the expansion will halt and the universe will begin to recollapse. At this point the universe is half of its final age. Distant galaxy's redshifts will switch to blueshifts. The cosmic background radiation starts heating up as the photons are blueshifted. Eventually the galaxies begin to merge together, the density goes way up, and the temperature increases. The universe ends in a ``big crunch.'' And that is it, as far as we know. The universe has a finite spatial extent and a finite time. In the open model, the universe is infinite in size and time, and it keeps expanding without end. Eventually each little group of galaxies lies basically alone in the cosmos as the other galaxies recede further and further away. The stars eventually die out, leaving behind cold dwarfs and black holes. Eventually the black holes might merge together into huge galaxy size black holes. The microwave background temperature goes down closer and closer to absolute zero. Things basically ``run down.'' So the choice of fates seems to be either the universe ends with a bang or a whimper.
How did the universe begin? It doesn't matter too much which of the three models we consider at this point; they all began pretty much the same, with a hot dense phase. Let's run time backwards from the present and see what happened in the past. As time runs backwards the galaxies approach each other as the universe shrinks back to its earlier, smaller size. We have estimated the age of our solar system to be about 5 billion years, but our sun is hardly the oldest star in the galaxy. The oldest stars are the Population II stars whose ages may be about 10 billion years. They may have formed at about the same time as our galaxy. Presumably other galaxies were forming at about this point in time. As previously discussed the halo stars and globular clusters, and the nuclear bulge probably formed first, followed by the disk of our galaxy. Galaxies in general must have formed out of great clouds of gas collapsing due to their own self-gravity. This is the time of galaxy formation throughout the universe and we are not really certain exactly when it was occurring, although it must be at a time on order 10 to 15 billion years ago, greater than half the time back to the beginning. In order to see forming galaxies we would have to look out through space to very distant objects with redshifts greater than 1. It is felt that the time of the quasars may be the age of galaxy formation and that the quasar phenomenon may be associated with young, forming galaxies. Bigger and more sensitive telescopes could go a long way toward addressing these questions.
Before the galaxies formed the universe was filled with gas, mostly hydrogen and helium, spread throughout space. Space was also filled with the background radiation except that the temperature was higher than the three degrees it is today. In fact the temperature goes up as the redshift, so that at a redshift of 1, about halfway back to the big bang in time, the temperature was 6 degrees, redshift of 2, 12 degrees and so on. At about a redshift of 1000, back to about one million years after the big bang, the temperature was 3000 degrees and this is hot enough so that the atoms of hydrogen are ionized. Earlier than this point in time the universe was like an HII region (emission nebula) everywhere, with hot ionized hydrogen interacting with the background photons. The universe at this time was a far different place from what it is today.
Back further in time the temperature and density both continue to climb as we get closer to the beginning. Most all the rest of the interesting activity takes place in the first three minutes of the universe. To describe this period of history let's begin with time zero and work forward.
We don't really know what the universe at time zero was like because all the visible universe would have been compacted into an infinitely dense singularity (like the point at the center of a black hole). We have no theory to describe such a thing. In such a state space and time lose there usual meanings. However, once we get forward in time to a tiny fraction of a second (say 10-40 of a second) we enter a time where we think that the universe can be described in terms of a theory of high energy physics. The appropriate theory would be something called a ``Grand Unified Theory" or GUT for short. This would be a theory that combined the separate strong nuclear, weak nuclear, and electromagnetic forces into one single force described by this one GUT theory. At the present time we don't have such a theory although physicists are trying to develop such a theory. Suffice it to say that at this point the universe is filled with energy (at huge temperatures, around 1025K) and possibly particles that are quite different from our present-day particles. It would be a very exotic state of things.
As we move forward in time, the temperature drops rapidly. Let's skip over most of the complexity and just summarize the highlights. Ordinary particles (i.e., protons and neutrons) would be formed somewhere around 10-5 seconds after the big bang, but there would be nearly equal amounts of matter and antimatter. As the temperature drops further, the antimatter and matter annihilate one another producing more photons. However, some excess matter is left over and it is that excess matter that goes on to become all the galaxies, stars, planets and you. It is a mystery why there should be some leftover matter, but obviously it was important to the rest of the history of the universe!
At about 1 second after the big bang the temperature of the universe is down to about a billion degrees. Things consist mainly of protons, neutrons and electrons, in addition to all the photons. At this point we have all the ingredients necessary for nuclear reactions and they take place during the next three minutes until the temperature drops below that suitable for nuclear reactions. During this time much of the hydrogen is turned into helium so that the final abundance to emerge from the big bang is one quarter helium and three quarters hydrogen. Some additional stuff is also made, like lithium and deuterium. Most of the helium in the universe is due to this primordial nucleosynthesis. The fact that there was so much helium in the universe used to be a puzzle; the stars are not efficient enough at cooking hydrogen into helium and further, even the oldest stars seemed to be a quarter helium. Big bang nucleosynthesis provides the answer.
Hubble's observation of the redshift distance relationship suggests that the universe is expanding, and the prediction of General Relativity that the universe cannot be static provides the theoretical background for understanding why the universe expands. The abundance of helium and the presence of the microwave background radiation provide direct evidence that our universe was once in a hot, dense state. These are the key elements of the big bang theory. Many refinements are possible and necessary. We don't know what the ultimate fate of the universe will be, nor do we have a theory for the very beginning of the big bang, i.e., right back to time t=0. Nevertheless the big bang model of the universe is one of the twentieth century's most remarkable and profound developments.
1999 - John F.
Hawley. These notes
are intended for the private, noncommercial use of students enrolled in
Astronomy.
Adpated
for Dept.
"Galaxies" by G.Petrov - 02'05.