REDSHIFTS
of GALAXIES
Content: Extragalactic distance scale, Photometric
redshifts
Adapted from The
Astronomy and
Astophysics
Encyclopedia and
B.F. Madore, W.L. Freedman, S.D.J. Gwyn et al.
1. EXTRAGALACTIC DISTANCE
SCALE
Calibration - STARS, CEPHEID VARIABLE, PERIOD-LUMINOSIRY
RELATION
In the early decades of this century, Henrietta S.
Leavitt recogned
that there is a statistical relationship between the average brightness
of a Cepheid variable star and the period of pulsation. The periods of
these stars range from a few days to a few hundred days,
and their luminosities (all of wliich are intrinsically much greater
than that of the Sun) span factors of several hundred in brightness.
In general, the longer the period of a Cepheid, the brighter is its
average thtnninc luminosity.
Because the period of pulsation can be measured
independently
of distance and because the apparent luminosity of a Cepheid
depends on the square of the distance, one can use the intnnsic
luminosity, as predicted by the period, in combination with the
apparent luminosity to derive a distance. As tcols in the extragalactic
distance scale, Cepheid variables provide one of the most accurate
means of determining distances to the nearby spiral and
irregular-tppe galaxies of the Local Group and somewhat beyond.
One very appealing attribute of Cepheid variables as a class of
distance indicators is that the physics for the Cepheid
period-luminosity relation is well understood. Put simply, all
self-luminous objects, including Cepheids, give off light in proportion
to both
their area and the surface brightness over that area. For spherical
bodies of radius R and surface temperature T, the total
luminosity L (integrated over all wavelengths) is found using
Stefan's law
where L =
4 R2
R2
 T4 and
T4 and
 the Stefan-Boltsmann
constant.
Furthermore, the fundamental period of oscillation P of any
mechanical system depends only on one thing, the mean density
the Stefan-Boltsmann
constant.
Furthermore, the fundamental period of oscillation P of any
mechanical system depends only on one thing, the mean density
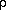 . Low-density
systems have longer periods of oscillation than high-density
systems, with the equation relating these two quantities having the
following form,
P
. Low-density
systems have longer periods of oscillation than high-density
systems, with the equation relating these two quantities having the
following form,
P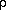 1/2
= Q, where Q is a constant.
Combining Stefan's law, the
P
1/2
= Q, where Q is a constant.
Combining Stefan's law, the
P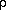 1/2
law, and an assumed
mass-luminosiry relation Indicates that the largest stars will have
the Inghest luminosities and the longest periods. And that is
exactly what is observed.
1/2
law, and an assumed
mass-luminosiry relation Indicates that the largest stars will have
the Inghest luminosities and the longest periods. And that is
exactly what is observed.
Of course, with a more rigorous (and more complex)
application
of physics, we can relax these simplifying constraints and redo the
calculations for stellar models havIng a reasonable range of mass
and with a variety of surface brightnesses. But these are refinements,
certainly necessary for detailed calculations, but not absolutely
necessary for an understanding of the underlying process leading to a
period-luminosity relation itself. The refinements do
tell us that the relation between period and luminosity will have
scatter, and that the scatter will have a physical origin due to
differences in surface temperature between stars of the same density
(i.e., same mass and radius), for it is temperature that determines the
surface brightness of sell-luminous objects. Ultimately, Cepheids are
well described by a PLC (period-luminosity-color)
relation.
It is of interest to note here that the physics that
applies to the
ensemble of Cepheid variables (that is to the periodluminosity
relation as a whole) also applies to the individual stars as they each
cycle through their oscillations. Radius variations in a single star
give rise to changes in area, which result in changes in luminosity;
surface temperature variations around the cycle drive changes in
the surface brightness which also affect the total luminosity. There
are again two parameters to the problem: The area is a geometrical
property of the star and therefore has the same effect on the
luminosity nearly independent of wavelength, whereas the surface
brightness, radiation theory tells us, is very sensitive to where in
the spectrum one observes the star. In the infrared, temperature
variations make only a slight contribution to luminosiry differences,
whereas in the blue and ultraviolet, the same temperature variations
can dominate the luminosiry variations. These changing
effects with wavelength can be seen in Fig. l
where the cyclical luminosity variation for a Cepheid is shown at
different wavelengths. In
the near ultraviolet the amplitudes are large and driven primarily by
surface temperature variations. In the far infrared
almost all of the luminosity change is a reflection of the radius
variation which is known to be out of phase and distinctly different
in shape with respect to the temperature variations.
 |
|
Figure 1. Typical light variations as a
function of phase for a Cepheid variable as observed at wavelengths
rangng from the ultraviolet (top light curve, labeled U) through the
blue, visual and red parts of the spectrum (labeled B, V, and R,
respectively) out to the near infrared (ending with the bottom light
curve at K = 2.2 µm). Note the decreasing
amplitude of the light variation, as well as the In shape and the shfft
In the phase of rnaxirnurn brightness as longer and longer wavelengths
are examilned.
|
The absolute calibration of the Cepheid
periodluminosity relation is
based on a small number of Cepheids found in galactic star clusters.
These clusters have independent distances, obtained from
main-sequence fitting techniques. Additionally, the same main-sequence
stars can be used to independently estimate the amount of Interstellar
dust obscuring and reddening the light of the
Cepheids. Unfortunately, the statistiqs are poor and the intrinsic
luminosities and colors of many of the cluster Cepheids are still
uncertain. Moreover, most field Cepheids are too far away to have
direct parallax measurements made with the present technology.
However, an independent calibration will be forthcoming when the
refurbished Hubble Space Telescope provides improved direct
determinations of the distance to the Large and Small Magellanic Clouds
in which hundreds of Cepheids, all essentially at the same distance,
will enter the calibration.
Unfortunately, the effects of interstellar reddening
due to intervening
dust both in our own galaxy and in the parent spiral galaxies of
extragalactic Cepheids can be quite severe and are very much
stronger.in the blue as compared to the red and Infrared. A
multicolored approach to the application of Cepheids to determining the
distance scale is therefore required. Using modern electronic detectors
(such as charge-coupled devices) and a variety of filters turning from
the blue to the very near infrared, this latest,
hybrid approach allows for both the distance and the total reddening to
individual external galaxies to be sirnultaneously solved for by a
careful application of the periodluniinosity relation, given an
a priori knowledge of the interstellar extinction law. Without a
determination of the extinction, all other distance estirnates are
upper limits, overestimating the true distance. Examples of
periodluminosity relations constructed by this technique can be
seen in Fig. 2 which consists of a
montage of
optical wavelength observations of Cepheids in the Large and Small
Magellanic Clouds,
followed by the dramatically narrower period-luminosity relations
found at infrared wavelengths. These latter relations are so well
defined and narrow that they have allowed astronomers to calculate not
only the distances to the Magellanic Clouds but also the
three-dimensional shape and orientation of these galaxies in space.
 |
|
Figure 2. Multiwavelength
period-luminosity relations for Cepheids observed in the Small
Magellanic Cloud (open circles) shifted into magnitude registry with
data for Cepheids in the Large Magellanic Cloud. Note the decreased
scatter as one goes from the blue wavelength data (at the top left of
the figure) to the near-infrared data (at the bottom right). The
individual PL relations are shifted vertically in magnitude and
horiitontally in period for display purposes only.
|
-
THE LOCAL (CEPHEID) DISTANCE SCALE
With the application of modern techniques to the
Cepheid
periodluminosity relation, it is now widely agreed that the
extragalactic distance scale is relatively secure for galaxies within,
and slightly beyond, the Local Group. For galaxies with Cepheids
identified and observed, the distance estimates, out to approximately 2
Mpc, are now agreed upon at the 10% level. However, a factor of 10
further away at 20 Mpc, where Cepheids have not yet been discovered,
the
uncertainty, as judged by rival factions, rises to a factor of 2
difference in opinion. Much of this uncertainty is expected to
disappear with the optically corrected imaging phase of the Hubble
Space Telescope expected to begin in late 1993 or 1994. One of the
major missions that MST is committed to working on is the
extragalactic distance scale. MST will be capable of discovering
Cepheids in galaxies that sample a much larger volume of space
than can ever be imaged from the ground (because of atmospheric
turbulence). A Cepheid-based distance to one or two galaxies at 20
Mpc (for instance in the Virgo Cluster, which is probably the
practical limit even for HST) will not end the controversy about
the size and age of the universe; but such observations will certainly
go
a long way toward narrowing the divergence of opinion. On the other
hand, with many more Cepheid-based distances to
galaxies Inside that volume lirnit, secondary distance indicators can
be calibrated with some statistical certainty, and these altemate
techniques can then be pushed deep into the extragalactic space
where the pure Hubble flow is expected to be revealed.
<>But the history of science
teaches us that even our most modest
expectations are not always met as we venture into new regimes.
To be sure, questions of importance, such as those concerned with
the age, size, and structure of the universe, will never completely go
away; given time they will only become more interesting. Without
Cepheid variables to lead the way in the extragalactic distance
scale, our view of the universe would certainly be far less secure
than we hope it is today.
2. PHOTOMETRIC
REDSHIFTS
The concept of photometric redshifts is not new. This essay provides
a brief history of photometric redshifts. The list of papers provided
below is not exhaustive; however, it does cover the development of the
technique up to about 1996. - S.D.J. Gwyn
Baum (1962)
was the first to
develop a technique for measuring redshifts photometrically. He used
a photoelectric photometer and 9 bandpasses spanning the spectrum from
3730Å to 9875Å. With this system he observed the spectral
energy distribution (SED) of 6 bright elliptical galaxies in the Virgo
cluster. He then observed 3 elliptical galaxies in another cluster
(Cl 0925+2044, also known as Abell 0801). By plotting the average SED
of the Virgo galaxies and the average SED of the Cl0925 galaxies on
the same graph using a logarithmic wavelength scale, he was able to
measure the displacement between the two energy distributions, and
hence the redshift of the second cluster. His redshift value of
z = 0.19 agreed closely with the known spectroscopic value of
z = 0.192, so he extended his technique to a handful of clusters
of then unknown
redshifts out to maximum redshift of z = 0.46. He then derived
a very
rough value of Omega_0. Baum's technique was fairly accurate, but
because of its dependence on a large 4000Å break spectral
feature,
it could only work on elliptical galaxies.
Koo (1985)
followed a different
approach. First, he used photographic plates instead of a photometer,
making it possible to measure photometric redshifts for a large number
of galaxies simultaneously. Second, instead of using 9 filters he
used only 4: UJFN (photographic U, BJ, RF and
IN). Third, instead
of using an empirical spectral energy distribution, he used the
theoretical Bruzual
(1983, among others)
no-evolution models for all
galaxy types.
The most important difference, however, was the way
the colours were
used. Instead of converting the photometric colours into a kind of
low resolution spectrum, he converted the Bruzual templates into
colours, and plotted lines of constant redshift and varying spectral
type, known as iso-z lines, on a colour-colour diagram. Finding that
the most normal colour-colour diagrams (e.g. U-J versus J-F and J-F
versus F-N) were degenerate in a range of redshifts, he invented what
he called colour-shape diagrams. The shape measured whether the SED
turned up or down at both ends, that is, whether the spectrum was bowl
shaped or humped. Another way to put it is that the colour measured
the first derivative with respect to wavelength of the spectrum and
the shape measured the second derivative. For colour he used either
2U-2F or U+J-F-N , both of which span a large wavelength range. For
shape, he used either U+2J-F or -U+J+F-N . Following this method to
measure the redshift of a galaxy, Koo calculated the colour and the
shape from the UJFN magnitudes and plotted them on the colour-shape
diagram. The redshift of the galaxy was then found by finding the
iso-z line closest to the point representing the galaxy. Koo tested
this method on a sample of 100 galaxies with known spectroscopic
redshifts ranging from z = 0.025 to z = 0.700.
This method is similar to that used by
Pello et al. (1996) and
Miralles, Pello & Le Borgne (1996).
They used the colours of
galaxies to determine ``permitted redshifts'' in the following manner:
The colors of galaxies are plotted as a function of redshift from the
Bruzual & Charlot (1993) models.
Each available color (with its
associated uncertainty) of a galaxy defines a ``permitted'' redshift
range on the corresponding color-redshift diagram. The intersection
of the permitted redshift ranges for all the colours determines the
redshift. This method was used by
Pello et al. (1996)
to discover a
cluster of galaxies at z > 0.75 by looking for an excess in
the redshift
distribution in the field of a gravitationally lensed quasar.
Miralles et al. (1996)
used the method to determine the redshift distribtion of the Hubble
Deep Field.
The ``ultra-violet dropout'' techniques of
Steidel et al. (1996) and
Madau et al. (1996)
are similar if simpler. All galaxy spectra have
a large Lyman break; shortward of 912Å, the continuum drops
dramatically. When this break is redshifted into and past the U
filter, the U flux is greatly reduced or non-existant, resulting in
very red ultra-violet colours.
In the ultra-violet dropout techniques, an exact
redshift of a galaxy
is not determined. Rather, the redshift is determined to be in the
redshift range where the Lyman break is in or just past the U filter.
Since U filters typically have a central wavelength of 3000Å,
this
works out to a redshift of z > 2.25. In practical terms,
redshifted
template galaxy spectra are used to determine a locus on a
colour-colour plot where most galaxies lie in a particular redshift
range. Those galaxies whose measured colours lie within the locus are
deemed to be in that redshift range. Clearly, this method is a lot
simpler than that of
Pello et al. (1996) as only two
colours are
considered. It is also a lot less precise as the redshift is not very
constrained. For both these reasons it is ideally suited for
pre-selecting galaxies at high redshift for spectroscopic
confirmation. Steidel et al. (1996)
did exactly this using the UGR
filters. Madau et al. (1996)
applied this technique to the Hubble
Deep Field using the F300W, F450W, F606W and F814W filters. The
technique was extended by using F450W dropouts to find galaxies of
redshifts z = 4.
The template fitting technique developped by
Loh & Spillar (1986b) more
closely resembles that of Baum (1962)
than that of Koo (1985).
Loh & Spillar (1986b)
observed 34 galaxies of known redshift in the
galaxy cluster 0023+1654 through 6 non-standard filters to test their
method. The standard deviation of the redshift differences
(zspec - zphot) was 0.12. They
went
on to use their technique to measure photometric redshifts for 1000
field galaxies in order to
determine a value for the density parameter,  0
(Loh & Spillar 1986a).
0
(Loh & Spillar 1986a).
Gwyn (1995)
tested this method using BVRI photometry of the Colless et
al. (Colless et al., 1990;
Colless et al., 1993) galaxies. The
larger uncertainty in photmetric redshifts thus derived
(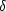 z
= 0.18) was attributed to the lack of a U filter. Numerous authors
(Gwyn and Hartwick 1996;
Lanzetta et al., 1996;
Mobasher et al., 1996;
Sawicki et al., 1996;
Cowie et al., 1996) have used this
technique to determine redshifts in the Hubble Deep Field.
z
= 0.18) was attributed to the lack of a U filter. Numerous authors
(Gwyn and Hartwick 1996;
Lanzetta et al., 1996;
Mobasher et al., 1996;
Sawicki et al., 1996;
Cowie et al., 1996) have used this
technique to determine redshifts in the Hubble Deep Field.
Prehaps the simplest and certainly the
most empirical photometric redshift technique yet is that of
Connolly et al. (1995a).
This method requires a ``training set'' of a large
number of galaxies with multi-color photometry and spectroscopic
redshifts. Redshift, z, is assumed to be a linear or quadratic
function of the magnitudes (Mi) of the galaxies,
i.e. if N is the number of filters:
 (1)
(1)
or
 (2)
(2)
The constants, ai and aij,
are found by
linear regression.
Connolly et al. (1995a)
used a UJFN plus redshift
data set extending to z = 0.5 of 370 galaxies. They showed that
this
method could determine redshifts with uncertainties of
 z = 0.057
with a linear fit and
z = 0.057
with a linear fit and  z
= 0.047 with a quadratic fit. There is
little or no loss of accuracy if colors (Ci = Mi -
Mi+1) are used
instead of magnitudes. Using this technique they were able to measure
the luminosity function out to J = 24 (SubbaRao et al., 1996).
z
= 0.047 with a quadratic fit. There is
little or no loss of accuracy if colors (Ci = Mi -
Mi+1) are used
instead of magnitudes. Using this technique they were able to measure
the luminosity function out to J = 24 (SubbaRao et al., 1996).
The advantage of the linear regression technique is
its extreme
simplicity. It has a few disadvantages: (1) A substantial collection
of spectroscopic redshifts must have been measured before the
technique can used. (2) Extension to fainter magnitudes or deeper
redshifts is not possible.
Compiled by G.T.Petrov, 2004
 R2
R2
 T4 and
T4 and
 the Stefan-Boltsmann
constant.
Furthermore, the fundamental period of oscillation P of any
mechanical system depends only on one thing, the mean density
the Stefan-Boltsmann
constant.
Furthermore, the fundamental period of oscillation P of any
mechanical system depends only on one thing, the mean density
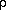 . Low-density
systems have longer periods of oscillation than high-density
systems, with the equation relating these two quantities having the
following form,
P
. Low-density
systems have longer periods of oscillation than high-density
systems, with the equation relating these two quantities having the
following form,
P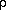 1/2
= Q, where Q is a constant.
Combining Stefan's law, the
P
1/2
= Q, where Q is a constant.
Combining Stefan's law, the
P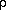 1/2
law, and an assumed
mass-luminosiry relation Indicates that the largest stars will have
the Inghest luminosities and the longest periods. And that is
exactly what is observed.
1/2
law, and an assumed
mass-luminosiry relation Indicates that the largest stars will have
the Inghest luminosities and the longest periods. And that is
exactly what is observed.


 0
(
0
(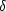 z
= 0.18) was attributed to the lack of a U filter. Numerous authors
(
z
= 0.18) was attributed to the lack of a U filter. Numerous authors
(
