LARGE SCALE STRUCTURE
Content: Superclusters, Voids,
Correlation function
Adapted
from P. Coles, 1999, The Routledge
Critical
Dictionary of the New Cosmology, G.Petrov et al.
1. SUPERCLUSTERS, OBSERVED PROPERTIES
Superclusters are large conglomerations of clusters
and groups of
galaxies on a scale exceeding 100 million light years [1021
km or 30 megaparsecs (Mpc)]. Individual superclusters and "complexes"
of
superclusters interconnect to form the largest known structures in the
universe: a sponge-like network of high-density regions , spaced apart
by a labyrinth of voids (Fig. 1). The
tendency
in recent years is for ever-larger structures to be recognized, so that
we may not have yet
established the top of the hierarchy of clustering, that is, the
largest inhomogeneities in the universe. The greatest strides have
been made since the mid-1970s, as large numbers of galaxy redshifts
have been obtained.
The first examinations of the large-scale
distribution of galaxies
were carried out in the 1930s independently by Edwin Hubble and Harlow
Shapley. Hubble worked in numerous narrow selected fields. Shapley
covered most of the sky using wide-angle photographs. He noted regions
where the galaxy count was much higher than average and labeled these
as "clouds" of galaxies. Many of his clouds are recognized today as
superclusters.
Improved wide-angle photographic surveys, such as
the classic
National Geographic Society-Palomar Observatory Sky Survey, do reveal
hundreds of thousands of galaxies, but give only a two-dimensional
view of their distribution. To some extent, the third dimension
(distance) can be gauged by the angular diameters of the galaxies. A
nearby galaxy appears larger than a more distant one, although one may
sometimes be misled by a small nearby galaxy mimicking the appearance
of a larger distant galaxy. However, there would be little problem in
deciding between nearby and distant clusters of galaxies. In this way,
in the 1950s and 1960s, George Abell and Fritz Zwicky independently
gauged the relative distances of clusters on the Palomar Sky
Survey. Abell concentrated on rich clusters, whereas Zwicky's cluster
boundaries lay far from the central condensations. Abell also noted
that certain regions of the sky had a greater number of clusters than
others. Thus, both suspected much larger entities. In a similar way,
C.D. Shane, working from Lick photographs, described "superclusters"
or (as he preferred to describe them, using Shapley's term) "clouds of
galaxies."
The true recognition of superclusters required a
three-dimensional
view. When distances to relatively nearby galaxies were calibrated,
Gerard de Vaucouleurs advocated the existence of a "supergalaxy," now
recognized as our local supercluster.
At larger distances, the most effective way of
obtaining galaxy
distances is to measure redshifts. Due to the overall expansion of the
universe, an observer in any galaxy would see its neighbors moving
away from it. The velocity of recession increases with distance from
the observer's galaxy according to Hubble's well known relation
V = H0 d ,
where V is the velocity of recession, d is the
distance,
and H0 is the
Hubble constant (in the range 50-100 km s-1 Mpc-1
or 15-30 km s-1 per
million light-years). The velocity can be measured by the Doppler
shift of spectral features (redshift): either absorption or emission
lines in the optical spectra, or 21-cm neutral hydrogen emission in
the radio region. knowing the velocity, the distance can be inferred.
Strictly speaking the observed velocity is not
entirely cosmological
but should be expressed as
V0 = H0 d + Vs
+ Vp ,
where the velocity V0 is now corrected for our Sun's
motion within the Galaxy and for the streaming motion of our galaxy, V0
is the streaming motion associated with the observed galaxy,
and
Vp is the observed
galaxy's own individual motion over and above systematic streaming;
Vp is significant (several hundred kilometers per
second) in rich
clusters. Because it is difficult to disentangle these velocities,
and because of the uncertainty in the value of the Hubble constant, it
is customary to plot data in "redshift space" (with dimensions shown
as kilometers per second) rather than in conventional
three-dimensional space. Gross structures are much the same in either
space, but the peculiar velocities in rich clusters make the clusters
appear stretched radially (the "Finger of God" effect) in redshift
space (examples of this can be seen in Fig. 2).
In the past, obtaining the spectrum of a single
galaxy called for a
photographic exposure of some hours duration. The advent of electronic
image intensifiers and the replacement of the photographic plate by
charge-coupled devices (CCDs) and Reticon arrays has greatly
accelerated the acquisition of redshifts. Around 1950 little more than
100 redshifts were known, by 1960, 1000 were known and twice that
number had been collected by 10 years later. Yet, by 1980 the figure
exceeded 10,000 and by 1990 it was around 40,000.
With greater numbers of redshifts available in the
mid-1970s, Guido
Chincarini pointed out that, even when clusters are avoided in a
study, redshifts seem to favor certain values and to avoid others (for
the region of sky involved). Thus superclustering was revealed in the
third dimension, and three-dimensional mapping became possible. Much
pioneering work was done in the region of the Coma cluster where a
bridge to a neighboring cluster, Abell 1367, was discerned, with a
void immediately in front of the structure.
In order to map completely the neighboring
superclusters to our own
"Virgo supercluster," one would need to work out to a redshift
corresponding to several thousand kilometers per second. Within such a
volume of space, there are hundreds of thousands of giant
galaxies. Even with present technology, it is quite impossible to
obtain all their redshifts (the number to be observed would be much
greater because a vast number of background galaxies would have to be
candidates). Thus, it is necessary to restrict observations to a
"representative" sample. The most common approach is to observe all
galaxies brighter than a selected limiting apparent luminosity
(apparent magnitude). Such a choice is satisfactory for the
capabilities of the telescopes involved, but nearer low-luminosity
galaxies are included in the sample, whereas distant high-luminosity
galaxies may be excluded. The data thin with distance, and low
galactic latitudes (where light from distant objects is subject to
extinction by matter in the MilKy Way) have to be
avoided. Nevertheless, knowledge of the galaxy luminosity function
(the relative numbers of galaxies versus luminosity) allows one to
derive true number densities and other statistics. Difficulties could
arise if the luminosity function varies with environment; such
tendencies have been claimed in the literature. The alternative
approach is to disregard a strict magnitude limit and to observe what
appears to constitute a representative sample on the sky. This allows
for initial mapping of superclusters (mainly because the intervening
voids are almost completely empty), but cannot produce quantitative
parameters. Whatever system of sampling is used, the outcome is plots
revealing filamentary or sponge-like structures, reminiscent of
aqueous media even though the data are in the form of discrete points.
Figure 1 gives an
indication of neighboring
superclusters. The nearest of these is the Hydra-Centaurus-Pavo
supercluster. The names
reflect the main constellations in which the structure is seen on the
sky (although constellations are based on nearby stars in our galaxy,
they conveniently represent general directions when looking far beyond
those stars). Although the Hydra-Centaurus portion is seen on the sky
on one side of the Milky Way and the Pavo portion on the other side,
the agreement in redshift and general continuity of structure point to
its being a single entity, with the main bulk lying in Centaurus or
probably behind the foreground obscuration of the Milky Way. The Hydra
condensation centers around the Hydra I cluster (redshift 3500 km
s-1) and there is only a relatively weak bridge to the
Centaurus
concentration. The latter is dominated by the Centaurus cluster, which
shows a composite structure in redshift space, with concentrations at
both 3000 and 4500 km s-1. However, the weaker 4500 km
s-1
concentration may be, to some extent, background galaxies because 4500
km s-1 is the dominant redshift for the bulk of the extended
Centaurus superclustering. The same redshift (4500 km s-1)
is picked up on the
Pavo side, which contains a number of weaker clusters. All these
clusters contain both elliptical and spiral galaxies, but the cores of
both Hydra I and Centaurus have greater proportions of elliptical and
SO galaxies. There seem to be some filamentary links between our own
Virgo supercluster and the Centaurus concentration, almost as if our
supercluster were something of an appendage. We are separated from the
Hydra and Pavo concentrations by foam-like voids with only a
sprinkling of galaxies around their perimeters.
The Coma supercluster, mentioned earlier, is
separated from our own
supercluster and Hydra-Centaurus by a number of voids. Its structure
is centered on the Coma cluster, the nearest rich cluster of galaxies
(composed almost entirely of elliptical and SO galaxies). From this
central concentration, extensions run out more or less perpendicular
to our line of sight. Although that running (west-wards) to the Abell
1367 cluster was the first discovered, present-day surveys
(particularly the Harvard-Smithsonian "slices") show it extending both
east, north, and southward, so much so that it has been referred to as
the Great Wall, and its full extent is still being assessed.
Although the Virgo, Centaurus, and Coma
superclusters dominate the
northern galactic hemisphere, the other side of the obscuring band of
the Milky Way is dominated by the Perseus-Pisces supercluster (which
has been mapped extensively by the radio redshifts of Martha P. Haynes
and Riccardo Giovanelli). Particularly interesting in this
supercluster is a filamentary central condensation that is well marked
by elliptical galaxies. It is some 4000 km s-1 long in
redshift space and runs perpendicular to the line of sight. Toward one
end lies the
Perseus cluster. Voids again intervene between this supercluster and
ours their peripheral galaxies provide tenuous
interconnections. Toward the south the supercluster continues and
connects to another heavy wall-like structure, in the Sculptor region,
that runs at an angle to our line of sight.
It has been remarked that these surrounding
structures give a sort
of "tree ring," appearance to the distribution within distances from
our galaxy that correspond to redshifts of several thousand kilometers
per second. More redshifts still are needed to define the nature and
extent of such larger patterns. What is relevant is that, whenever a
volume of space is sampled, there always seems to be structure with a
dimension comparable to that of the volume surveyed. This has led to
considerations of fractal structures (identical forms repeated on
ever-increasing scales) occurring in the universe. If this is correct,
although one would gain a geometrical interpretation to the nature of
the structures, it would make a physical explanation extremely
difficult.
- MORE DISTANT SUPERCLUSTERS
Beyond redshifts of several thousand kilometers per
second, a number
of further superclusters have been mapped tentatively. The volume is
incompletely sampled, although it is unlikely that very conspicuous
superclusters would have been overlooked. For example, in the north
there is a pair of superclusters in Hercules (at redshifts around
10,000 km s-1), whereas in the south Shapley's cloud of
galaxies in
Horologium is resolved into two superclusters (at redshifts of 12,000
and 18,000 km s-1) seen along a common line of sight (see
Fig. 2).
An alternative approach for reaching out to larger
distances is to
assume that Abell's clusters, which mark peak number densities, flag
the high points of superclusters. Thus, distant superclusters can be
recognized as groupings (in redshift space) of Abell clusters, and
examinations of even larger volumes of space can be carried out. On
this basis, ever larger conglomerations (to scales of 30,000 km s-1)
have been claimed. The work recently has been extended to the southern
skies.
The future holds exciting prospects. Just as human
eyes scanned the
galaxies on the wide-angle photographs, the finest-quality photographs
of the U.K. Schmidt telescope and the new Palomar sky surveys are now
being scrutinized by machine and millions of galaxies already have
been detected and cataloged. From these sky densities comes evidence
of possible larger superclusters. In parallel, the development of
fiber-optic spectrographs that can be used to observe many galaxies
simultaneously may lead to the mass determination of redshifts. We can
look forward to finding even more remarkable structures in the
superclustering of galaxies.
2. VOIDS
Definition
of the problem
In extragalactic astronomy, the basic unit is a galaxy with a
characteristic
length of 20 kpc that typically moves
within a group
or clusters with diameter 50 kpc to 5 Mpc which in turn is located in a supercluster
with diameter 50 Mpc or larger. Superclusters
and voids are often discussed together because they are identified and
studied
on a common data base and it is likely that they share a common origin
and represent
two complementary effects of related evolutionary processes.
The structure of superclusters, the material entities that make
up the contiguous
shell, was reviewed by Oort,
1983,
and the voids by Rood, 1988. Voids were not immediately
recognized
in the surface distribution of galaxies because they are superimposed
by
background and especially foreground galaxies.
Voids were
recognized only after Doppler velocities were measured for
statistically homogeneous
samples of galaxies in selected solid angles of the sky, which provided
direct information
on the three-dimensional distribution of galaxies.
In extragalactic
astronomy, the three-dimensional region that constitutes a void is
transparent
and empty or nearly empty of galaxies. It is often useful to think of a
void as
for a discrete entity - a region containing significantly fewer
galaxies than predicted
by the appropriate Poisson distribution. The occurrence of physical
groupings
of galaxies evidently requires the presence
<>of
voids defined in this way. There are two ways
in which to study an individual void observationally:
a) the void can
be probed
with telescopic sensors in order to detect galaxies within it
b) the structure and
content of the contiguous shell of superclusters
surrounding the void can be studied.
Early surveys of
galaxies over large solid angles of the sky indicated a superclustering
of galaxies, i.e. predominant occurrence of galaxies, groups, and
clusters within
larger structures now called superclusters
(Lundmark, Holmberg, Shapley,
Oort, de Vaucoleurs,
Shane & Wirtanen, Abell).
<>From independent
counts of galaxies to faint magnitudes in a large number of small
survey fields
distributed over the sky, Hubble concluded that groups and clusters of
galaxies
are aggregations drawn from the general field, which is everywhere and
in all
directions approximately uniform.
<>
Early studies of the
surface distribution of galaxies featured three different models:
a) superclustering
of galaxies
b) super-large rich
clusters
c) group and clusters
drawn from a uniform general field.
To discriminate
between these models, we need to know the three-dimensional
distribution of galaxies
in large homogeneous samples.
<>Chincarini &
Rood, 1970 pointed
out in the constellation Hercules the redshifts segregate into a small number of
groups. They hypothesized
that galaxies occur in groups and that the apparent field of galaxies
in two dimensional
distribution is the result of a
superposition of such
groups - model (a).
<>
Peebles, 1975 showed the Universe
conforms to model (a), the
superclustering of galaxies, based on
correlation functions
derived from the surface distribution of galaxies over large solid
angle of the
sky.
<>
Studying the
correlation function from large sets of data, Peebles
et al., 1980,
found that galaxies and systems of galaxies are correlated on all
scales up to
the noise limit of their data, between approx 10 and 100 Mpc.
The results are
consistent with (a) and (b) but not with
(c).
<>
Oort,
1983 pointed out a large
void in Hercules from the analysis of data from 1976 - 1981. In fact
“VOID” is
a natural contraction of “region devoid of galaxies”.
<>
Vetolani
et al., 1985 failed to
detect a nonclustered homogeneous
background of galaxies
from the three-dimensional distribution of galaxies with mp < 14.5
covering
a large solid angle in the sky. Their result is consistent with the conclusions
of Soneira
& Peebles, 1977.
<>
There are many
works to confirm the presence of the voids in theoretical aspect. As
early as
1970, Zeldovich et
al., 1977,
developed theoretical models showing the "cell-like" large-scale
structure
formed by nonlinear dissipative collapse of gaseous density
perturbations,
forming "pancakes", followed by condensation into galaxies.
<>
Einasto
et al, 1978 found that the
observed large-scale three-dimensional distribution of galaxies
exhibits
cellular structure in accordance with Zeldovich
et
al. models.
<>
Many cosmologists
in Western Europe and USA assumed that galaxies formed initially by
Jeans
instabilities from random density perturbations that evolved into a
hierarchy
of larger structures that could be tracked by N-body computer
experiments.
<>
Ikeuchi,
1981, and Ostriker
& Cowie,
1986, suggested that cosmic explosions with an energy release
10^61
ergs would create blast waves that might trigger or amplify the
formation of
galaxies, and that might also produce large-scale structure
by tending to create voids with outward moving
galaxies on their contiguous shells.
<>
Johnson S.B. et. al., 1994 take CCD images of the Bootes
void. Several
dozen galaxies have been found within this void. However a 4,000 km/s
diameter
volume displaced to the southwest of the original void center remains
completely empty raising the possibility that the true void is at a
lower
declination and is
smaller than originally
defined. There is a deficit of
galaxies over roughly a four magnitude range centered on M* at the
distance of
the void center.
<>
Bahckal
N.A., 1995 represent the
SDSS. The Sloan Digital Sky Survey (SDSS) will provide a complete
imaging and
spectroscopic survey of the high-latitude northern sky. The 2D survey
will
image the sky in five colors and will contain nearly 5x10^7 galaxies to
approx
23m. The spectroscopic survey will obtain spectra of the brightest 10^6
galaxies, 10^5 quasars, and 10^3 rich clusters of galaxies (to approx
18.3-19.3
m, respectively). The survey will identify a complete
sample of several thousand rich clusters of
galaxies, both in 2D and 3D - the largest automated sample yet
available.
The extensive
cluster sample can be used to determine critical clustering properties
such as
the luminosity-function, velocity-function, and mass-function of
clusters of
galaxies (a critical test for cosmological models), detailed cluster
dynamics
and Omega_dyn, the cluster correlation
function and
its dependence on richness, cluster evolution, superclustering
and voids to the largest scales yet
observed, the motions of clusters and their large-scale peculiar
velocity
field, as well as detailed correlations between X-ray and optical
properties of
clusters, the density-morphology relation, and cluster-quasar
associations. The
large redshift survey, reaching to a depth
of >600,h^-1 Mpc,
will accurately map the
largest scales yet observed, determine the power-spectrum and correlation
function on these large scales
for different type galaxies, and study the clustering of quasars to
high redshifts (z > 4). The
implications of the survey for cosmological
models, the dark matter, and Omega are also discussed.
<>
Lindner U.,
1996 investigate the
distribution of normal (faint) galaxies and blue compact galaxies (BCGs) in voids by analyzing their distribution
as a
function of distance from the void centers and by employing nearest neighbour statistics between objects of various subsamples. They find that galaxies in voids
defined by brighter
galaxies tend to be concentrated close to the walls of voids in a
hierarchical manner, similar to the
behavior of brighter galaxies. The behavior of BCGs
is in this respect similar to the one found for normal dwarf galaxies.
<>
Ryden
B.S. and Mellot A.L., 1996 compare the properties of voids in real space
to their properties in redshift space.
Both the void probability
function (VPF) and the underdense
probability
function (RE) are enhanced in redshift
space. With
their algorithm that detects individual voids, voids are ellipses whose
enclosed density of galaxies falls below a threshold density. When voids are identified
using this algorithm, the mean void size and the maximum void size both
increase in going from real space to redshift
space.
<>
El-ad H. et
al., 1996 present a new
void search algorithm for automated detection of voids in
three-dimensional redshift surveys. Based
on a model in which the main
features of the large-scale structure (LSS) of the universe are voids
and
walls, they classify the galaxies into wall galaxies and field
galaxies, and define
voids as
continuous volumes that are devoid of any wall
galaxies. Field galaxies are allowed within
the voids. The algorithm makes no assumptions regarding the shapes of
the
voids, and the only constraint that is imposed is that the voids are
always
thicker than a preset limit, thus eliminating connections between
adjacent
voids through small breaches in the walls.
<>
El-ad H. and Piran T., 1997 present the VOID FINDER algorithm, a novel tool for
objectively
quantifying voids in the galaxy distribution. The algorithm first
classifies
galaxies as either wall galaxies or field galaxies. Then, it identifies
voids
in the wall-galaxy distribution. Voids are defined as continuous
volumes that
do not contain any wall galaxies. The voids must be thicker than an
adjustable
limit, which is refined in successive iterations. In this way, we
identify the
same regions that would be recognized as voids by the eye. The voids
have a
scale of at least 40,h^-1 Mpc
and an average -0.9 underdensity. Faint
galaxies do
not fill the voids, but they do populate them more than bright ones.
<>
Kuhn B. et
al., 1977 present the
results of a search for intrinsically faint galaxies towards three
regions with
known voids and the Hercules supercluster.
They point
out that no clear indication of a void-population was found.
<>
Popescu
C.C. et al., 1997 analyse
the spatial distribution of our sample of ELGs
in comparison with the distribution of normal galaxies.
Overall both distributions trace the same structures. Nevertheless they
also
found a few ELGs in voids, from which at
least 8 lie
in the very well defined nearby voids. The isolated galaxies seem to
form
fainter structures that divide the larger voids into smaller ones. From
their
estimations of the expected number of void galaxies they did not find
an
underlying homogenous void population.
<>
El-ad H. and Piran T., 2000 present a comparison between the voids in two nearly all-sky
redshift surveys: the Optical Redshift
Survey (ORS) and the IRAS 1.2-Jy survey. While the galaxies in these
surveys
are selected differently and their populations are known to be biased
relative
to each other, the two void distributions are similar.
<>
Grogin
N.A. and Geller M.J., 2000
analyze the optical properties of approx 300 galaxies within and around
three
prominent voids of the Center for Astrophysics Redshift
Survey determining CCD morphologies and H_alpha
equivalent widths from their imaging and spectroscopic survey. Both the
morphological mix and the H_alpha line
width
distribution of galaxies at modest underdensities,
0.5<n/n _d1le1, are
indistinguishable from the control sample at modest overdensities,
1<n/n_d1le2. Both density regions contain a similar fraction of
galaxies
with early-type (E and S0) morphologies and with
absorption-line spectra (approx35%). In the voids, where the luminous
galaxies presumably
formed more recently, there should be more gas and dust present for
active star
formation triggered by nearby companions.
<>
Friedmann Y. and Piran T., 2001
introduce a simple model for the formation of
voids. In this model the underdensity of
galaxies in voids
is the product of two factors. The first arises from a gravitational
expansion
of the negative density perturbation. The second is due to biasing:
galaxies
are less likely to form in an underdense
region.
<>
Schmidt J.D.
et al., 2001 show the
sizes and shapes of voids in a galaxy survey depend not only on the
physics of
structure formation, but also on the sampling density of the survey and
on the
algorithm used to define voids. Using an N-body simulation with a tauCDM power spectrum, they study the properties
of voids
in samples with different number densities of galaxies, in both redshift space and real space. When voids are
defined as totally
empty regions of space, their characteristic volume is strongly
dependent on
sampling density; when they are defined as regions whose density is 0.2
times
the mean galaxy density, the dependence is less strong.
<>
Petrov G.,
A. Kniazev and J.
Fried, 2004
presented photometry
and morphology of faint galaxies in the direction of 1600+18 in Hercules
void. Coordinates
of ca. 1200 faint galaxies in a field of one square degree centered at
1600+18 (1950) (Hercules
void), and m(B),diameters, position
angles and morphological classification are presented. The
distribution of the magnitudes of the galaxies in this direction is
compared
with “Log Normal” and “Gauss” ones and with similar results from SDDS studies of
galaxies. Major
axes luminosity profiles are analysed. Some candidates for primeval galaxies - Low
surface brightness galaxies were detected in the direction of
the void.
The superclustering of
galaxies (model “a”) and the presence of
voids are now accepted as fact, a paradigm among workers on large-scale
structure.<>
<>
Amongst the famous known
voids are Coma and Hercules, which are practically devoid of matter,
whereas Bootes and Perseus-Pisces
are not
empty (approx 10 emission line galaxies in Boo, furthermore evidence
for
obscuring matter).
<>The structure of superclusters,
the material entities that make up the
contiguous shell, as pointed by Oort,
allows us to
study the vicinity of the voids itself.
Particularly
interesting are correlations of spectral properties of galaxies and
Hubble morphological
type with local density of galaxies.
3. CORRELATION FUNCTION
The testing of theories of structure formation
using observations of the large-scale structure of the
distribution of
galaxies requires a statistical approach. Theoretical studies of the
problem of structure formation generally consist of performing
numerical N-body simulations on powerful computers. Such
simulations show how galaxies would form and cluster according
to some
well-defined assumptions about the form of primordial density
fluctuations, the nature of any dark matter and the
parameters of an
underlying cosmological model, such as the density parameter
and
Hubble constant. The simulated Universe is then compared with
observations, and this requires a statistical approach: the idea is to
derive a number (a `statistic') which encapsulates the nature of the
spatial distribution in some objective way. If the model matches the
observations, the statistic should have the same numerical value for
both model and reality. It should always be borne in mind, however,
that no single statistic can measure every possible aspect of a
complicated thing like the distribution of galaxies in space. So a
model may well pass some statistical tests, but fail on others which
might be more sensitive to particular aspects of the spatial
pattern. Statistics therefore can be used to reject models, but not to
prove that a particular model is correct.
One of the simplest (and most commonly used)
statistical methods
appropriate for the analysis of galaxy clustering observations is the
correlation function or, more accurately, the two-point
correlation
function. This measures the statistical tendency for galaxies to
occur
in pairs rather than individually. The correlation function, usually
denoted by 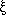 (r),
measures the number of pairs of galaxies found at a separation r
compared with how many such pairs would be found if
galaxies were distributed at random throughout space. More formally,
the probability of finding two galaxies in small volumes
dV1 and dV2
separated by a distance r is defined to be be
(r),
measures the number of pairs of galaxies found at a separation r
compared with how many such pairs would be found if
galaxies were distributed at random throughout space. More formally,
the probability of finding two galaxies in small volumes
dV1 and dV2
separated by a distance r is defined to be be
dP = n2 (1 + 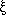 (r)) dV1 dV2
(r)) dV1 dV2
where n is the average density of galaxies
per unit volume. A positive
value of 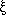 (r)
thus indicates that there are more pairs of galaxies with a separation
r than would occur at random; galaxies are then said
to be clustered on the scale r. A negative value indicates that
galaxies tend to avoid each other; they are then said to be
anticlustered. A completely random distribution, usually called
a
Poisson distribution, has
(r)
thus indicates that there are more pairs of galaxies with a separation
r than would occur at random; galaxies are then said
to be clustered on the scale r. A negative value indicates that
galaxies tend to avoid each other; they are then said to be
anticlustered. A completely random distribution, usually called
a
Poisson distribution, has 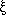 (r) = 0 for all values of r.
(r) = 0 for all values of r.
Estimates of the correlation function of galaxies
indicate that
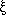 (r)
is a power-law function of r:
(r)
is a power-law function of r:
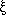 (r)
(r) 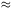 (r/r0)-1.8
(r/r0)-1.8
where the constant r0 is usually
called the
correlation length. The value of r0 depends
slightly on the type of galaxy
chosen, but is around 5 Mpc for bright galaxies. This behaviour
indicates that these
galaxies are highly clustered on scales of up to several tens of
millions of light years in a roughly fractal pattern. On larger
scales, however, 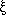 (r) becomes negative, indicating the presence of
large voids (see large-scale structure). The correlation function
(r) becomes negative, indicating the presence of
large voids (see large-scale structure). The correlation function
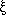 (r)
is mathematically related to the power spectrum P(k) by
a Fourier
transformation; the function P(k) is also used as a descriptor
of
clustering on large scales.
(r)
is mathematically related to the power spectrum P(k) by
a Fourier
transformation; the function P(k) is also used as a descriptor
of
clustering on large scales.
Compiled by G.T.Petrov, 2004
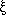 (r),
measures the number of pairs of galaxies found at a separation r
compared with how many such pairs would be found if
galaxies were distributed at random throughout space. More formally,
the probability of finding two galaxies in small volumes
dV1 and dV2
separated by a distance r is defined to be be
(r),
measures the number of pairs of galaxies found at a separation r
compared with how many such pairs would be found if
galaxies were distributed at random throughout space. More formally,
the probability of finding two galaxies in small volumes
dV1 and dV2
separated by a distance r is defined to be be
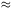 (r/r0)-1.8
(r/r0)-1.8